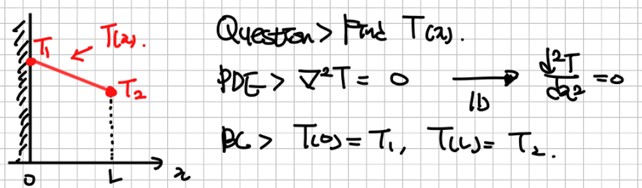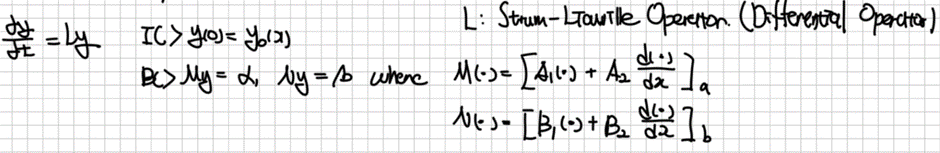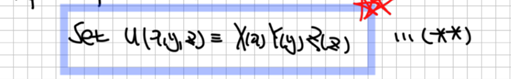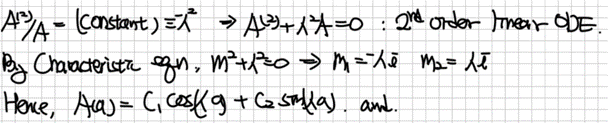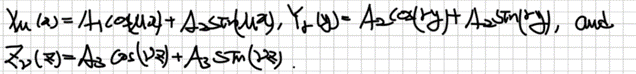화공노트: 화학공학 살펴보기

화공에서의 양자화학

양자화학에 대한 내용은 화학과의 ‘물리화학2’, 물리학과의 ‘양자물리학’에서 배울 수 있으나, 이번에 오랜만에 화학공학과에서도 강의가 개설되었습니다. 화학공학과에서 양자화학은 재료 및 소자 등을 이해할 때 필요합니다. 예를 들어 Density Function Theory를 기반으로 한 Simulation은 촉매, 흡착제, 전극 등 다양한 부분에서 물질의 특성을 예측을 하는데 사용됩니다. 이 부분에 대한 모든 지식을 배울 수는 없겠지만, 이들을 이해하기 위해 알아야 할 최소한의 지식을 배울 수 있는 과목입니다.

 양자역학의 관점으로 물질의 특성을 이해하기 위해 다음 순서로 과목을 공부합니다.

 1) Introduction to Quantum Mechanics

양자역학이 고전역학과 다른 점이 무엇인지, 그리고 양자 역학을 설명할 수 있도록 하는 몇 가지 가설에 대해 배우게 됩니다 그리고 전자가 관여하지 않은 상황에서의 Schrodinger Equation을 풀이해보며 파동함수를 이용한 system의 해석 방식에 대해 배우게 됩니다. 그리고 원자내 전자는 핵을 중심으로 한 대칭성을 갖기에, Spherical Coordiate에서의 Schrodinger Equation은 어떻게 풀이하는지, 그리고 결과들이 어떠한 의미를 갖고 있는지 배우게 됩니다.

 2) Electrons on Atom

가장 단순한 형태의 원자인 수소에 대한 Schrodinger Equation을 풀이해보며, 실제 전자가 전자기적 상호작용 하에 있을 때 어떠한 차이가 있는지 배우게 됩니다. 한편, 전자가 2개 이상 있는 원자들을 기존의 방식을 이용해서 해석해보고자 Perturbation Theory 등을 배우고 그 결과에 대해 이해해봅니다. 한편, 고등학교 때나 일반화학 때 배우는 전자배치 규칙(쌓음의 원리, 파울리 배타 원리 등)과 오비탈의 모양 등을 좀더 자세하게 배워볼 수 있습니다.

 3) Electrons on Molecule

마찬가지로 가장 단순한 형태의 분자로부터 분자 오비탈을 이해하기 위해 파동함수를 설정하는 방법과 이를 풀어내는 과정, 그리고 그 결과를 해석해볼 수 있습니다. 이를 하기 위해 필요한 Galerkin Method와 같은 수학적 기법을, Self-Consistent Approximation과 같은 개념적 이해를 함께 배우기도 합니다. 처음에는 전자가 1개만 있는 분자에 대해 배우지만, 나아가서는 두 개의 전자, 또는 더 복합적은 구조의 분자를 이해하고자 Hartree-Forck Method나 Density Function Theory까지 배우게 될 것입니다.

공부할 때 신경 쓰면 좋은 점

1) 자신만의 주 교재 참고하기

강의계획서를 보면 교수님께서 따로 주교재나 부교재를 기재해주지 않은 것을 확인할 수 있을 것입니다. 교수님께서 최대한 많이, 그리고 반복해서 내용을 전달하시려고 신경 쓰지만, 그럼에도 텍스트를 통해서 이해가 필요한 순간이 있더라고요. 물리학과에서 사용하는 Griffiths의 교재도 좋지만, Atkins의 물리화학 교재(11ed) CH 7부터 수록된 내용들이, 강의 순서와 더 잘 맞을 것입니다. 해당 교재가 말해주고 있는 의미와, 교수님이 표기하는 수식을 연결해서 공부하면 도움이 될 것 같습니다.

 2) 수식의 나열이 의미하고자 하는 바 놓치지 않기

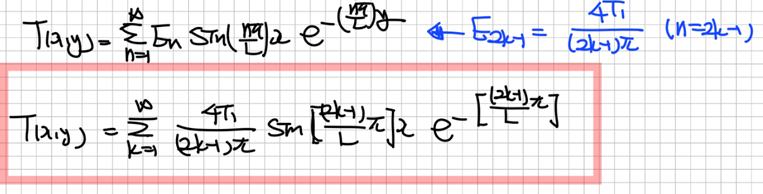
수식이 굉장히 많이 등장합니다. 적분기호를 표기하지 않기 위해 배우는 (dirac) Bracket notation도 처음에는 생소할 수 있습니다. 행렬, 그리고 미분방정식 관점에서 Eigenvalue Problem을 풀이하기도 하고요. 최진훈 교수님의 화공수학 내용에서 배운 관점들이 오히려 양자화학을 공부하는데 도움이 되던 때도 종종 있었습니다. 나열되어 있는 수식들 속에서, 이를 통해 하고자 하는 것이 무엇인지 놓치지 않는 것이 중요합니다. 결국 Schrodinger Equation이 Eigenvalue Problem이기에, 원하는 변수들을 반영한 파동함수를 찾고, 그 해당함수의 eigenvalue에 해당하는 에너지를 찾는 것을 계속해서 반복하게 될 것입니다.

공정열역학에서 다루는 내용

공정열역학은 화공열역학에서 다루지 못한 다성분계에 대한 내용을 다루고 있습니다. 화공열역학2라고 생각하면 편할 것 같습니다. 공정열역학이 전공선택 과목으로 분류되어 있지만, 화학과, 물리학과, 그리고 기계과에서 다루는 열역학보다는 더 자세한 이야기를 다루는, 타 과의 열역학과 화공과의 열역학을 구분 짓는 과목이라 생각됩니다. 물리화학의 CH 4 ~ CH 6 내용을 조금 더 깊게 다룬다고 생각하면 편할 것 같습니다.

공정열역학을 수강하면 다음의 내용들을 주로 배우게 됩니다.

1) Equilibrium

다성분계에서의 열역학에서는 처음으로 Equilibrium에 대해 배우게 됩니다. 특히, 화공에서 주로 사용되는 Vapor Liquid Equilibrium을 배우게 됩니다. 다성분계라고 이야기했지만, 실제로는 주로 2개 성분 혼합물의 평형에 대해 배우게 되며, 여러 Diagram을 통한 정성적인 이해부터, (Modified) Rault’s Law를 통한 정성적인 계산을 하게 됩니다. 정성적인 계산을 할 때 각 상황에 대한 반복계산법도 접할 수 있습니다. 한편, 평형점이 아닌 지점에서의 system의 구성을 평가할 수 있는 Flash Calculation을 배우면서 해당 부분을 마무리하게 될 것입니다. 학기 말에는 Vapor Liquid-Liquid Equilibrium 등 조금 더 복잡한 평형 상태에 대해 배울 기회가 있습니다.

2) Solution Thermodynamics

단일성분계에서의 열역학을 배울 때 온도, 압력, 부피 등의 변화에 대한 엔탈피, 엔트로피 등의 물성 변화를 수식을 이용해서 나타내는 작업을 했을 것입니다. 다성분계에서도 비슷한 작업을 할 수 있으며, 이를 위해 fugacity, activity 등의 개념을 도입하게 됩니다. 이 부분을 공부할 때는 이상적인 순/혼합물, 그리고 실제 순/혼합물에서 fugacity와 activity가 어떻게 표현되는지 잘 구분하며 공부를 하면 도움이 될 것입니다. 이를 기존에 배운 Residual Property와 새롭게 도입하는 Excess Property와 연관 지으며 물성들 사이의 관계를 표현하고, 이를 예측하는 방법에 대해 배우게 될 것입니다. 학기 말에는 이러한 Fugacity 등을 반복계산법을 이용해서 정량적으로 계산하는 내용도 배우게 됩니다.

3) System with Reaction

화학공학은 반응이 일어나는 system을 다루는 경우가 많기에, 실제 반응이 진행될 때의 system을 해석하는 방법을 배우게 됩니다. 일반화학이나 물리화학에서 배운 평형상수를 fugacity, activity 등을 이용해서 정량적으로 계산하는 방법에 대해 배우고, 르 샤틀리에의 원리에 따라 온도 및 압력 변화에 대한 반응 상수의 변화를 보다 정밀하게 추정하는 방법에 대해 배우게 됩니다.

시험 준비 및 공부할 때 유의할 점

1) 공정열역학 과목에서 다루는 계산

화공열역학때 배웠던 계산 방식을 그대로 활용하게 됩니다. 반복계산법을 통해서 수렴하는 값을 찾아내거나, 내삽을 통해서 임의의 상태에 대한 물성을 추론하는 식으로요. 이 부분은 어쩔 수 없이 연습이 많이 필요하다 생각됩니다. 다만, 계산을 진행할 때 풀이 과정을 잘 정돈해서 작성하거나, 또는 자신 나름의 규칙대로 작성을 한다면 수치들을 대입할 때 도움이 되었던 것 같습니다.

2) 증명의 방향성을 생각하고 수식 전개하기

생각보다 개념을 서술해야 하는 문제도 많이 출제가 됩니다. 식 전개 내용을 모두 암기하는 것이 아니라, 증명의 시작점과 목표 그리고 사이사이 수식을 전개하기 위해 필요한 개념만 기억하여 암기량을 최소화하려 했던 것 같습니다.

반응공학에서 다루는 내용

화학과와 화학공학과를 구분 지을 때 가장 먼저 언급되는 과목입니다. 반응이 관여한 물질수지식을 기반으로 원하는 효율을 낼 수 있는 반응기를 설계하는 방법에 대해 배우는 과목입니다. 배우는 내용을 간단히 소개하고자 합니다.

1) Mole Balance and Stoichiometry

양론에서 배웠던 물질수지식에 반응이 관여되었을 때 어떻게 변화하고, 각 반응기에서 물질수지식이 어떻게 표현되는지에 대한 내용을 배우게 됩니다. 이를 더 잘 표현하기 위해 Conversion(전환율)을 배우고, 반응계수의 비율에 맞추어 각 물질의 몰 농도를 표현하는 방법에 대해 배울 수 있습니다.

2) Reactor Designing for Single/Multiple Reaction

이를 이용해서 원하는 목표에 해당하는 반응기의 크기를 결정하는 방법에 대해 배우게 됩니다. Levensipel Plot이라는 것을 배워 그래프를 이용해서 크기를 정하는 방법, Conversion을 이용해서 결정하는 방법, Molar Flow를 이용해서 구하는 방법 등이 존재합니다. 특정 반응기, 반응의 개수에 따라 사용할 수 있는 방법이 다르고, 이를 적절히 선정해서 반응기의 종류, 개수, 크기 등을 결정하는 방법에 대해 배울 수 있습니다.

공부방법

1) 정말 많이 연습해보기

3학년 때 배운 과목 중 문제풀이와 개념 사이의 간극이 컸던 과목이었습니다. 많은 문제를 조건에 맞추어 풀어보는 것 밖에 방법이 없는 것 같습니다. 대표적인 교재로 Fogler와 Levenspiel이 있는데, 주 교재가 아닌 다른 교재에서 문제를 출제하는 경우가 있기에 다른 교재들을 참고하는 것도 도움이 됩니다. 특히 Fogler의 경우 인터넷 홈페이지에서 CD-ROM 문제를 열람할 수 있는데, 해당 부분에서 출제가 많이 되었던 것으로 기억합니다.

2) 어디까지 손으로 풀어낼 수 있는지 기준 잡기

Multiple Reaction에 대한 반응기의 경우 대부분 정량적으로 식을 정리하고, 이를 프로그램을 통해 풀이하라고 솔루션에 기재가 되어 있습니다. 그렇기에 맥이 빠질 수 있긴 하지만.. 그럼에도 식들을 정리하는 연습을 해두는 것이 중요합니다. 차수의 변경, 문제 조건의 추가 등으로 손으로 풀지 못하는 문제가 풀이가 가능해지는 경우도 있기 때문입니다.

3) 적절한 가정 이용하기 (특히 과량의 반응물)

문제풀이를 단순히 하기 위해 받아들여질 만한 가정들이 사용되곤 합니다. 대표적으로 A+B->C 2차 반응이지만 과량의 B에 대한 A의 반응으로 B가 거의 일정한 pseudo-1st order reaction 등으로 해석하는 방법이 있습니다. 이처럼 문제풀이를 단순화할 수 있는 방식을 나름대로 가정해보고, 자신의 가정이 맞는지 재검토해보아 문제를 최대한 단순화해서 접근하는 연습이 필요합니다.

열 및 물질전달에서 다루는 내용

화공유체역학에서 운동량 전달에 대한 내용을 배웠다면, 열 및 물질전달에서는 열전달과 물질전달에 대해 배웁니다. 서로 달라 보이는 두 분야는 수학적으로 풀이 방식이 닮아 있으며, 이를 Analogy라고 말하기도 합니다. 열물전의 공부 순서는 (1) 해당 system의 열 또는 물질 전달 현상을 설명할 수 있는 지배방정식을 세우고, (2) 이를 풀기 위해 필요한 경계/초기 조건들을 설정한 후 (3) 식을 직접 풀이하거나, 해석할 수 있는 가장 단순한 형태로 정리하는 과정을 반복하게 될 것입니다. 조금 더 자세히 설명 드리고자 합니다.

0) Introduction to Heat Transfer

열전달의 3가지 메커니즘인 Conduction(전도), Convection(대류), 그리고 Radiation(복사)에 대한 기본적인 개념을 공부할 수 있습니다. 그리고 열전달 현상을 서술하는데 알아야 할 Energy Balance Equation, Heat Flux와 여러 Energy에 대한 개념을 잡을 수 있습니다.

1) Conduction: Molecular Heat Transfer

처음은 열전달의 첫 번째 메커니즘은 Conduction(전도)에 대해 배웁니다. 전도는 인접한 분자의 떨림을 전달하며, 높은 온도에서 낮은 온도로 열에너지를 전달하는 열전달 방식입니다. 이를 전자회로의 옴의 법칙을 이용해서 해석하듯, 열의 흐름을 온도차와 열전달 저항을 이용해서 설명하는 ‘Circuit Analogy’에 대해 배우게 될 것입니다. 이를 Cartesian, Cylindrical 그리고 Spherical 좌표계에서 표현하는 법을 배우고, Energy balance Equation을 이용해서 Temperature Profile 구하는 방법을 공부해볼 수 있습니다.

Energy balance 식은 동일하나 그 식이 쓰여진 상황에 따라 해는 달라지는데, 이를 결정하는 Initial/Boundary Condition에 대해서도 배울 수 있습니다. 처음에는 1D, 2D Steady State에 대해 공부하며 시간을 고려하지 않은 열전달에 대해 배우지만, Unsteady State의 열전달을 공부하며, 시간에 대한 온도 분포의 변화에 대해 공부해볼 수 있습니다.

2) Convection: Convective Heat Transfer

Conduction이 인접한 분자 진동에 의해 에너지를 전달하는 방식이라면, Convection은 유체 자체의 이동으로 열에너지가 전달되는 방식입니다. 그렇기에 유체의 흐름에 대해 이해할 필요가 있으며, 표면 근처의 유체 거동을 설명하는 Boundary Layer(경계층) 개념을 처음 배우게 됩니다. 이를 수학적으로 해석하기 위해서 변수들의 Nondimensionalization(무차원화)를 진행하기도 하고, Variable Combination or Transformation(변수들의 조합 및 변환)을 진행하기도 합니다. 이 과정에서 정의되는 Nondimensional Number이 물리적인 의미에 대해서도 배울 수 있습니다.

한편, Convection에 의한 열전달 정도는 Newton’s Cooling Law에 의해 결정됩니다. 이때 External Flow(외부유동)과 Internal Flow(내부유동)에서의 열전달계수를 결정하는 방법을 배울 수 있습니다. 특히 Internal Flow의 개념을 이용해서 Heat Exchanger에 대한 개념도 배울 수 있습니다.

3) Mass Transfer: Analogous Concept compared to Heat Transfer

한편, 물질전달도 molecular/convective transfer 메커니즘을 따라 발생할 수 있으며, 전자의 경우를 Diffusion, 후자의 경우를 Convective Mass Transfer이라고 합니다. 열전달과 물질전달, 사실 운동량 전달까지 수학적으로 동일한 형태를 지니고 있지만, 표기법이나 경계조건 등에서 약간의 차이를 보입니다. 그렇기에 해당 부분에서는 물질전달을 설명할 수 있는 Species Mass Balance Equation의 작성방법과, Initial/Boundary Condition의 작성 방법에 대해 배울 수 있습니다.

공부방식

전공필수의 거의 마지막 과목이기에 많은 분들이 어려워하는 것 같습니다. 특히 이동현상 분야 자체가 눈에 보이지 않는 대상들을 수학적으로 모델링하고 풀이해보는 내용을 다루고 있기 때문입니다. Conduction과 Convection 내용의 공부 방식이 약간 다를 수 있기에, 나누어서 설명을 하고자 합니다.

1) Conduction: 경계조건 설정이 처음이자 끝

Conduction의 경우 system을 설명하는 지배 방정식이 완전히 동일합니다. 그렇기에 system을 설명할 수 있는 Boundary/Initial Condition을 올바르게 설정하는 것이 제일 중요합니다. Boundary는 결국 System의 경계를 말하기에, 해당 지점에서 온도는 일정한지, 열흐름이 일정한지, 열흐름이 없는지 등을 파악하고 이를 수학적으로 잘 풀어내면 온도 분포를 쉽게 구할 수 있습니다. 화공유체역학에서 Navier Stokes Equation의 풀이와 동일한 방식이며, 해당 부분을 복습하는 것도 도움이 될 수 있습니다.

2) Convection: 정성적 해석과 정량적 해석의 구분

Convection의 경우 Fluid Velocity Profile과 Temperature Profile을 동시에 얻어야 하기에 식을 풀이해서 얻는 경우는 거의 없습니다. 대신 Nusselt Number라는 무차원수를 이용해서 열전달계수를 얻어내고, 이를 통해 열 전달 정도를 결정할 때가 많습니다. 어떠한 조건에서 해당 식들을 사용할 수 있을지를 잘 정리해두는 것이 중요합니다.

그렇다고 몇 개의 식을 외우는 것으로 해당 단원들의 공부를 끝내서는 안됩니다. Velocity Profile로부터 Temperature Profile을 얻어내는 과정을 이해하고, 이때 쓰인 가정들은 무엇인지, 그 결과가 갖는 물리적 의미는 무엇인지를 중심으로 공부를 할 필요가 있습니다.

전기화학에서 다루는 내용

화공에서 이차전지, 반도체 등 전류/전자와 관련된 소자에 대한 연구가 활발히 진행됨에 따라 인기가 높아진 과목입니다. 전기화학에서는 전자의 운동이 관여된 system에 대한 열역학 그리고 이동현상에 대해 배우게 됩니다. 교수님께서 선수지식을 설명해주시지만, 새롭게 배우는 것과 나름대로 알고 있는 것과는 차이가 있을 것이기에, 4학년에 수강하는 것도 나쁘지 않다고 생각됩니다.

전기화학 과목에서는 다음의 내용들을 다룹니다.

1) Introduction to Electrics

일반물리학2의 전반부에서 배우는 전자기학의 기초 내용을 배웁니다. Columb’s Law로부터 Electric Field, Electric Potential 등 논의를 위해 알아야 하는 용어들을 정의하고 관련된 내용들을 배웁니다. 전류가 전자의 이동으로 나타난 것과 비슷하게, 전하를 띠는 입자가 이동해서도 전류가 발생할 수 있습니다. 이를 표현하기 위해 mobility, transparent number 등과 같은 개념도 새로 배우게 될 것입니다.

2) Thermodynamics with Electrics

열역학은 상태의 변환이 가능한지, 변환이 가능하다면 해당 상태 변환에 필요한 에너지 등을 계산해내는 분야라고 생각합니다. 전기화학에서의 열역학은 기본적으로 다성분계로 구성이 되어있기에, 이 부분에 대한 내용을 먼저 배우게 됩니다. 특히 성분이 많아지며 나타나는 비이상성을 나타내기 위해 activity라는 개념에 대해 상세히 배우고, 이를 이용해서 이온을 표현하는 방법에 대해서도 배울 수 있습니다.

이를 바탕으로 전지의 기본 단위인 Cell에 대해 자세히 배우게 됩니다. Cell의 종류는 무엇인지, Cell 내의 전극은 어떻게 정의하는지, 이들의 관계에서부터 예상되는 깁스에너지와 전압의 크기 등을 게산하는 방법에 대해 배우게 됩니다. 개인적으로 가장 헷갈리는 부분이었지만, 그만큼 중요했던 내용이었습니다.

3) Kinetics and Transport Phenomena with Electircs

열역학을 가능성의 학문이라 이야기한 이유는, 그 과정에서 소요되는 시간에 대해 고려하지 않기 때문입니다. 전류는 전극에서의 산화환원 속도에 의해 결정되고, 단위 시간당 이동한 전자의 양으로부터 전류가 얻어집니다. 이를 계산할 수 있는 Butler-Volmer Equation에 대한 내용을 배우게 됩니다. 한편, 해당 전류는 평형에서 벗어난 상태에서 발생하며 벗어난 정도를 overpotential을 이용해서 표현합니다. overpotential이 발생하는 이유와, 각 상황에서 전류나 반응물의 농도 등이 어떻게 변하는지에 대해서도 배워볼 수 있습니다.

4) Transport Phenomena with Electrics

지금까지는 cell 전체에서, 그리고 전극 근처에서의 내용에 대해 다루었습니다. 이러한 현상들은 사실 Cell 내부에서 물질들이 이동하기에 관찰됩니다. 그렇기에 물질의 이동, 특히 이온의 이동에 대해 자세하게 내용을 다루게 됩니다. 이온은 Migration, Diffusion, 그리고 Convection에 의해 이동할 수 있습니다. 각 물질 이동 방식에 따른 물질의 농도 분포 등을 계산하는 방법에 대해 배우게 됩니다. Migration의 경우 Nernst-Plank Equation을 이용해서 풀이하고 Diffusion의 경우 Fick’s 2nd Law를 라플라스 변환을 이용해서 풀이하게 될 것입니다. 한편, Convection의 경우 이를 이용하는 Rotating Electrode 등에 대한 내용을 배울 수 있을 것입니다.

5) Other Themes

남은 수업시간에는 전기화학과 관련된 여러 주제들에 대해 배우게 됩니다. 물질의 전기화학적 거동성을 평가하기 위해 진행하는 Voltammetry 기법과, 전기화학현상을 이용한 여러 측정장치, 그리고 이차전지의 기본 개념 등을 배울 수 있습니다. 아마 학기 중 진도에 맞추어 교수님께서 조정하실 것입니다.

시험 준비방식 및 공부 방법

공부해야 하는 양이 적지 않았던 것 같습니다. 매주 배운 내용을 복습하기 위해서 주말 하루를 다 썼던 것 같습니다. 6학점짜리 과목이라는 말을 어디선가 봤던 것 같은데, 공감이 많이 되었습니다. 그렇다고 시험 자체가 어렵게 나오지는 않습니다. 강의자료에 있는 내용을 그대로 물어보는 문항이 대부분이고, 일부 문항이 교수님께서 수업시간에 말로 설명해주신 내용에서 출제되기 때문입니다.

1) 교재를 적극적으로 활용하기

교수님의 강의자료가 꼭 필요한 내용만 담겨있긴 하지만, 불친절하다고 느낄 수 있습니다. 그 여백들을 수업시간에 말씀해주긴 하지만, 교재를 봤을 때 이해가 되었던 부분이 많았습니다. 특히 Transport 부분의 내용은 주교재가 아닌 부교재에서 많이 언급되므로, 이를 참고하면 도움이 됩니다.

(1) 주교재 Keith Oldham, Electrochemical Science and Technology

(2) 부교재 Thomas-Alyea, Electrochemical System

(3) 참고교재 Atkins, physical chemistry - Debye Huckle Theory나 Mobility 등을 공부할 때 좋았습니다.

2) 식 변환은 편리함을 위해 이루어짐을 믿기

정말 많은 식들이 나오고, 모든 식의 결과를 외울 수 없기에 시험 시간에 어쩔 수 없이 유도를 해낼 수 있어야 합니다. 연필과 종이를 이용해서 연습을 하다보면 이걸 왜 해야 하는지 의문이 들 수도 있습니다. 이러한 변환과 유도는 계산에 편리함을 주기 위해 진행됩니다. 예를 들어 대칭성을 활용하기 위해 spherical coordinate를 도입하거나, 전극 근처에서의 농도는 측정이 어렵기에 다른 지점에서의 농도를 대입해서 변환하는가 하는 이유 등에 대해 배울 수 있습니다. 식을 적을 때 이를 고려하면 공부를 하는데 더 편했던 기억이 납니다.

3) 헷갈리는 내용은 그 주에 해결하기

화공에서 전기적 내용에 대해 다룰 기회가 많이 없기에, 부호규약이나 개념적으로 헷갈리는 내용들을 종종 접하게 될 것입니다. 전공과목들은 앞의 내용을 알고 있다고 전제하고 있기 때문에 복습을 하든, 예습을 미리 하든 최대한 그 주에 해결하는 것을 권장합니다. 그렇지 않다면, 수업시간이 시간낭비로 느껴질 수 있습니다.

1. 화공유체역학에서 다루는 내용

인터넷에 역학을 찾아보면, 물체의 운동에 관한 법칙을 연구하는 한 분야라고 정의하고 있습니다. 그렇기에 유체역학은 유체(fluid)의 운동에 관한 법칙을 이해하고, 이들을 설명하는 방법에 대해 배울 수 있음을 기대할 수 있습니다. 화공에서 유체역학은 ‘운동량전달’로 불리기도 합니다. 힘이 운동량 변화를 나타내기에 유체의 이동이 가져오게 되는 힘의 변화, 반대로 외부 힘(펌프 등)에 의한 유체 이동의 변화 등에 대해 고민해볼 수 있습니다. 이 관점이 기계과와 화공에서의 유체역학의 가장 큰 차이라고 생각합니다.

화공에서 유체역학을 배울 때 다음 3가지 내용을 공부하게 됩니다.

(1) Macroscopic Property Transport: Mass, Momentum and Energy Conservation on Control Volume

양론에서 Governing Equation이라는 이름으로 A=I-O+G-C를 배웠을 것이라 생각합니다. 어떤 시스템에서 물질들의 축적, 유출입, 반응에 의한 생성/소모 등의 흐름은 변하지 않기에, 이 관계를 이용해서 여러 문제들을 공부했을 것입니다. 이 수지식(Balance Equation)은 물질에만 국한하는 것이 아닌, system(Control Volume)을 설명하는 다양한 물성들에 대해서 성립합니다.

Reynolds Transport Theorem(레이놀즈 수송 정리, RTT)는 유체의 흐름이 동반하는 물성들의 변화와 보존을 설명하고, 이때 고려하는 물성에는 유체의 질량, 선 및 각운동량, 에너지가 있습니다. 과목 초반에 유체 정역학(Fluids Statics)을 배우는데, 이는 운동량의 변화가 힘이기 때문입니다. 외부에서 작용하는 힘이 운동량 전달에 주는 영향을 고려하고자 배우는 것입니다. 많이 들어본 베르누이 방정식은 사실 레이놀즈 수송 정리 중 에너지 보존에 의해 설명되는 식이기도 합니다.

(2) Microscopic Property Transport: Distribution of Velocity on Control Volume

레이놀즈 수송정리는 물성들의 macroscopic transport만 설명할 수 있습니다. Control Volume에 유/출입하는 유체에 의해 전달되는 물성의 변화를 설명할 수 있지만, 그 내부에서 어떤 변화를 갖는지 알지 못하기 때문입니다.

이를 설명하고자 Navier Stokes Equation(나비에 스토크스 방정식)을 배우게 됩니다. Control Volume의 differential element에서 관찰되는 운동량의 변화를 관찰하고, 이를 풀어서 velocity distribution을 얻을 수 있게 됩니다. 속도 분포를 알게 된다면, shear stress(전단응력) 등 특정 위치에서의 나타나는 현상들을 더 잘 이해할 수 있게 됩니다.

(3) Fluid Flow Property on Various Situation: External and Internal Flow

표면과의 상호작용으로 인해 유체는 표면 근처에서 Boundary Layer이라는 것을 형성합니다. 그렇기에 파이프의 내부 또는 유체 내 장애물 위를 흐르는 유체의 거동에 대해 추가로 공부하게 되고, 이때 주로 마찰에 대해 고려하게 됩니다. 관내 유동에서는 Friction Factor(마찰계수), 외부 유동에서는 Drag Force Coefficient(항력계수)라는 이름으로 표면에 작용하는 유체의 stress 등에 대해 공부하게 됩니다.

2. 공부할 때 참고하면 좋을 것들

1) 주 교재에 의존하지 않기

화공유체역학의 주 교재로 Wilkes를 사용하는데, 개인적으로 좋은 책이라는 생각은 들지 않습니다. 설명이 불친절하기도 하고, 연습문제도 지나치게 어려운 느낌이 있기 때문입니다. 아래의 교재들을 참고하는 것이 더 도움이 될 것입니다.

(1) McDonalds ‘Fluid Mechanics’ - 유체 역학 개념이 잘 서술되어 있는 책

(2) Welty ‘Fundamentals of Momentum, Heat and Mass Transfer’ - 유체역학 흐름 잡기에 좋은 책

(3) Bird ‘Transport Phenomena’ - 운동량 전달 중 특히 Shell Balance 부분을 공부하기 좋은 책

(4) 한국화학공학회 ‘이동현상 응용과 해법’ - 나비에 스토크스 방정식을 활용할 수 있는 다양한 예제 수록

2) 부호 규약과 변하지 않는 특성의 구분

일반물리1을 수강하며 free body diagram을 그리며, 힘의 방향에 대해 고민해본 적이 종종 있었을 것이라 생각됩니다. 유체역학도 유체와 관련된 힘을 다루기에 부호 규약이 나오게 되고, 주로 shear stress(전단응력)을 공부할 때 헷갈리는 때가 있을 것입니다. 기계공학과 화학공학에서 바라보는 유체역학의 개념이 상이하기에, 여러 교재들을 참고하면 부호에 차이가 있게 됩니다. 해당 부호 설정이 가져오는 물리적인 의미를 고민하며 공부를 하면 도움이 될 것입니다.

3) 주요한 단위에 대한 고민

유체역학을 공부하면 여러 단위들을 접하게 됩니다. 특히 점도를 설명하기 위한 Poisson(P)과 GCS(gram, centimeter, sec) 단위 등을 새롭게 접하게 될 것입니다. 이들을 기존에 알고 있던 단위들과 변환에 익숙해 지는 것도 필요한 연습 중 하나가 될 것입니다.

Contents Preview

타원형 편미분방정식의 2번째 예시입니다. 2차원에서의 열전도, 그 중에서도 한 방향으로 매우 긴 평면에서의 열전도에 대해 다루어보겠습니다.

2차원 타원형 편미분방정식 (1) 매우 긴 평면에서의 열전도 (2D Elliptic PDE: Conduction on Infinitely Long Thin Plane)

문제 상황은 다음과 같습니다.

$y$ 방향으로 매우 긴 평면에서 어떻게 전도가 일어나는지 살펴보는 문제입니다.

우선 경계조건을 살펴보겠습니다. $x$ 방향에 대한 경계조건은 제차의 형태를 따르고 $y$ 방향에 대한 경계조건은 비제차인 것으로 보입니다. 그렇기에 $x$ 방향에 대해 고유함수를 구하고, 나중에 $y$ 방향에 경계조건으로 고유함수의 계수를 결정지으면 될 것 같습니다.

변수분리법으로 문제 풀이를 시작하겠습니다.

Step 1 변수분리법을 위한 변수의 분리

온도가 각각 $x$와 $y$의 조합으로 표현될 수 있다고 생각하고 식을 다시 정리할 수 있습니다. $x$와 $y$에 관한 식을 얻을 수 있는데 이는 둘 다 일정해야 합니다. 경계조건도 다시 작성됩니다.

우리가 원하는 것은 자명하지 않은 해(nontrivial solution)입니다. 값이 0으로 나타나는 해 또는 조건을 원하지 않습니다. 이를 이용해서 각 변수에 대해 조건을 다시 작성했습니다.

Step 2 고윳값$\lambda$과 고유함수 찾기

2개의 상미분방정식에 대해 자명하지 않은 해가 존재하기 위한 고윳값을 찾아야 합니다. 이를 위해 고윳값의 부호마다 해가 존재할 수 있는지 살펴봐야 합니다.

이때 x에 대해 고윳값을 결정하고 고유함수를 찾을 것입니다. 왜냐하면 y는 비체자 경계조건을 갖고 있기 때문입니다.

X에 대한 식은 2차 선형 상미분방정식이며, 이는 특성방정식(characteristic equation)을 이용해서 풀이할 수 있습니다.

고윳값이 양수일 때부터 살펴보겠습니다.

(1) 고윳값이 양수일 때 $\lambda > 0$

경계조건을 편하게 적용하기 쉽게 쌍곡선함수(Hyperbolic Function)를 이용해서 식을 정리했습니다. 실제로 조건을 대입해본 결과 두 계수 A, B가 모두 0이 되며 이는 0만 해가 될 수 있음을 의미합니다. 따라서 고윳값이 양수일 때는 자명한 해(trivial solution)밖에 얻지 못하므로 다른 경우를 생각해야 합니다.

(2) 고윳값이 0일 때 $\lambda = 0$

고윳값이 0으로 중근을 가지면, 라그랑쥐의 차수축소법(Reduction of Order)을 사용해서 새로운 해를 얻을 수 있습니다. 여기에 경계조건을 적용하면 계수 A, B가 모두 0입니다. 따라서 이 경우도 우리가 원하는 고윳값이 될 수 없음을 알게됩니다.

(3) 고윳값이 음수일 때 $\lambda < 0$

해를 얻고 오일러 항등식(Euler’s Identity)을 이용해서 삼각함수로 해를 다시 작성한 것입니다. 경계조건을 대입해봤을 때 코사인함수에 대한 계수는 0이지만, 사인함수는 그 자체로 0이 될 수 있으므로 자명하지 않은 해를 얻을 수 있습니다.

사인함수가 0이 될 수 있는 상황을 생각해서 풀이하면, 이 스트름-리우빌 문제에 대한 고윳값과 고유함수를 얻을 수 있습니다.

Step 3 $Y(y)$ 결정하기

Step 2에서 찾은 고윳값을 이용해서 $y$에 대한 고유함수도 얻을 수 있습니다.

모든 경계조건을 적용할 필요는 없습니다. 결국 마지막에 고유함수에 대한 계수를 결정할 때 사용해야 하기 때문입니다. 다만 $y$가 무한대로 갈 때의 경계조건이 0, 즉 수렴하기 위해서는 계수 $C$가 0이 되어야 하며, 이를 반영해서 고유함수를 얻을 수 있습니다.

Step 4 각 변수에 대한 해의 조합

문제를 통해 $x, y$에 대한 해를 얻었으므로, 원래의 해를 찾기 위해 다시 조합할 수 있습니다. 하지만 고유함수에 대한 조합은 특정 $n$에 대한 해이므로, 일반화된 해를 찾기 위해 시그마를 취해줍니다.

이제 마지막 단계로 다가갑니다. 과연 고유함수에 대한 계수를 어떻게 정의해야 하는지에 대해서 말이죠.

이는 남은 경계조건의 사용, 그리고 내적으로 보이는 고유함수의 직교성을 활용해서 얻을 수 있습니다.

Step 5 고유함수의 계수 $E _n$결정

문제를 구하기 위해 사용하지 않은 경계조건을 활용합니다. 그리고 식을 정리하기 위해 내적을 취합니다. 고유함수의 직교성 때문에 자기 자신에 대한 내적을 제외한 항들은 모두 0으로 소거된 결과를 얻을 수 있습니다. 이를 정리하면 다음과 같습니다.

이제 분수, 분모를 계산해서 계수를 구체화할 수 있습니다.

특별할 것 없는 계산이지만, 코사인함수에 대한 식이 n에 따라 특정 값을 따르는 것을 이용해서 식을 단순하게 만들 수 있습니다.

삼각함수의 반각공식으로 알려진 관계를 이용하면 식을 정리할 수 있습니다.

Step 7 해의 결정

각각에 대한 고유함수, 그리고 해를 알게 되었으므로 문제에서 구하라는 $x, y$에 대한 온도 분포를 알 수 있게 되었습니다. 계산 결과는 아래와 같습니다.

타원형 편미분방정식의 두 번째 예제인 매우 긴 평면에서의 열전도를 살펴봤습니다. 다음 예제는 크기가 정해져 있는 평면에서의 열 전도의 결과로 어떠한 온도 분포가 나오는지를 살펴보도록 하겠습니다.

감사합니다.

Contents Preview

이제부터 편미분방정식을 본격적으로 풀이하게 됩니다. 사실 변수분리법(Separation of Variables)을 이용해서 상미분방정식 문제로 바꿔주는 원리는 동일합니다. 다만 설정된 경계조건의 형태에 따라 문제를 풀이하는 과정이 다양할 뿐입니다. 그렇기에 여러 문제를 풀어보는 것이 중요합니다. 타원형 쌍곡선을 풀이하는 것은 라플라스 방정식(Laplace Equation)을 풀이하는 것이며, 3가지 예제를 가져왔습니다. 이 방정식 풀이의 이해에 도움이 되었으면 합니다. 이번 글에서는 1차 열전도를 살펴볼 것입니다.

1차 타원형 편미분방정식 (1D Elliptic PDE)

문제 상황은 다음과 같습니다.

1차원, 즉 x 방향으로의 전달만 고려하는 문제입니다. 1차 라플라스 방정식은 상미분방정식의 형태를 따르므로 일반해를 구하고, 주어진 경계조건으로 적분상수만 결정해주면 됩니다.

문제에서 요구하는 답을 구할 수 있고, 어떤 선형함수를 따라 온도가 바뀌는 것을 알 수 있습니다.

Contents Preview

공학수학에서 편미분방정식을 풀이할 때 경계조건이 제차(Homogeneous)인 경우를 많이 제시해줍니다. 어떤 경우에는 비제차 경계조건(Inhomogeneous Boundary Condition)이 제시된 경우도 많습니다. 이때는 고유함수의 선형조합으로 일반해를 나타내지 못합니다. 따라서 이번 글에서는 비제차 경계조건이 제시되었을 때 이를 해결하는 방법에 대해 살펴볼 것입니다. 이 방법을 경계조건의 제차화(Homogenization of Boundary Condition)라고 말하기도 합니다.

비제차 경계조건 문제는 다음과 같습니다.

어떤 일반화된 경계조건에 대해 그 결과가 0이 아님을 확인할 수 있습니다. 그렇기에 이 상황에서 우리가 문제를 풀이한다 하더라도 일반해를 얻을 수 없습니다.

해의 형태를 아래처럼 가정했을 때, 경계조건을 제차 형태를 따르도록 만들 수 있습니다.

원래 방정식의 해가 제차형태일 때의 해와 어떤 steady-state(equilibrium) 즉, 시간을 따르지 않는 해의 조합으로 쓰인다고 생각한 것입니다. 비제차 2차 선형 상미분방정식을 풀이하기 위해 우선 제차일 때의 해를 구하고, 그 다음 특수해를 구했던 것과 거의 유사한 것을 알 수 있습니다.

이제 이를 원래의 방정식에 대입해서 정리해보겠습니다.

어떤 평형상태(steady-state)에 대한 해를 구하고, 이를 제거하면 제차 형태를 따르는 경계조건을 구할 수 있게 됩니다.

지금까지 편미분방정식의 종류 및 판단방법, 변수분리법, 그리고 비제차 경계조건을 갖는 문제에 대한 해결방법까지 살펴봤습니다. 다음 글 부터는 각각의 편미분방정식을 어떻게 풀이해야 하는지 그 과정에 대해 자세하게 다루어보려고 합니다.

감사합니다.

Contents Preview

상미분방정식을 설명하는 많은 일반해들이 있습니다. 편미분방정식은 그렇지 않습니다. 아직 잘 설명된 일반해는 없고, 단지 알려진 풀이 방법만 존재할 뿐입니다. 편미방을 풀이할 수 있는 몇가지 방법이 있습니다. 공학수학을 배울 때는 변수분리법(Separation of Variables)을 처음 접하게 되기에, 이를 이용해서 편미방을 푸는 방법에 대해 살펴보겠습니다.

읽기 전에 보면 좋은 글

12. 스트룸 리우빌 이론(Strum-Liouville Theory) 예제: 푸리에 사인 급수 :: 화공노트: 화학공학 살펴보기 (tistory.com)

6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 :: 화공노트: 화학공학 살펴보기 (tistory.com)

변수분리법을 이용한 편미분방정식의 풀이

1) 의의

우리는 왜 변수분리법을 사용하게 되었을까요? 이를 이용하면 n차원 편미분방정식을 n개의 상미분방정식의 풀이로 문제상황을 바꿀 수 있습니다.

2) 적용

3차원 라플라스 방정식을 예로 들어보겠습니다. 3차원 편미분방정식이므로 아마 3개의 상미분방정식 풀이로 바뀔 것입니다.

풀이 과정을 단계별로 살펴보겠습니다

Step 1 종속변수에 관여한 변수들을 분리한다.

해가 각 변수에 대한 함수의 조합이라고 생각하는 것에서 풀이를 시작합니다. 저희는 현재 3차원 라플라스 방정식을 다루고 있기에 $x, y, z$ 3가지 변수가 관여할 것입니다. 그렇기에 위처럼 변수를 분리할 수 있습니다.

Step 2 식의 재작성

식 (**)를 식 (*)에 대입해서 정리할 수 있습니다.

$X, Y, Z$ 중 하나라도 0이 되면 해도 0이 되므로, $XYZ$는 0이 될 수 없습니다. 이를 이용해서 식을 정리한 것입니다.

Step 3 가정을 통한 상미분방정식으로의 문제 전환

식 (***)의 각 항들은 모두 일정한 값을 가져야 합니다. 이 이유에 대해 설명하겠습니다.

편미방의 해가 각각 독립적인 변수에 대한 함수의 조합으로 표현된다 생각하고 문제를 풀이하고 있습니다. 만약 이 세 개의 항 중 하나라도 상수가 아니라면, 하나의 변화로 인해 나머지 항들의 값도 따라 변하게 됩니다. 세 항의 합이 일정하기 때문입니다. 즉, 이 세 항 중 하나의 항이라도 일정하지 않다면, 독립적인 변수에 대해 식을 설정한 전제에 대해 모순이 발생하게 됩니다. 따라서 각각의 항들은 모두 일정한 값을 따라야 합니다.

각 항들을 일정한 상수로 두고 문제풀이를 이어가겠습니다.

위의 과정을 따라 식을 정리할 수 있습니다. 지금은 어떤 음수로 일정할 것이라고 가정했지만, 주어진 경계조건에 따라 다른 부호의 값을 따르는 경우도 있습니다. 원래는 그냥 어떤 상수로 일정하다고 두면 되겠습니다.

정리하자면, 변수분리법을 통해 식을 정리하면 3차원 편미분방정식이 3개의 상미분방정식을 풀이하는 문제로 바뀐 것을 알 수 있습니다.

Step 4 상미분방정식의 풀이와 해의 조합

현재 풀어야 하는 미분방정식은 선형 제차 상미분방정식이기 때문에 특성방정식(characteristic equation)을 풀이하면 해를 쉽게 얻을 수 있습니다.

A를 X, Y, Z를 대표하는 변수로 두었기에 각 변수에 대한 해도 표현할 수 있습니다.

각 변수에 대한 해를 얻었으니, 이들을 다시 곱하면 원래 해를 얻을 수 있습니다.

Step 5 선형결합을 통한 방정식의 해 구하기

우리가 위에서 얻은 해는 특정 고윳값에 대한 고유함수입니다. 이 편미분방정식이 선형이고, 주어진 경계조건이 모두 제차(homogeneous)라면 선형조합을 통해 주어진 구간을 설명할 수 있는 해를 구할 수 있습니다.

Step 6 계수의 결정

위에서 얻은 해는 모든 경계/초기조건이 결정되지 않은 해입니다. 그렇기에 주어진 초기/경계조건을 활용해서 고유함수의 계수를 결정해야 합니다.

이는 고유함수의 직교성을 이용해서 구하게 되며, 이를 위해 내적을 활용합니다. 주어진 조건들에 따라 계수가 다르게 결정될 것이고, 주어진 문제를 설명할 수 있는 특정해를 얻게 됩니다.

지금까지 변수분리법을 활용해서 편미분방정식을 풀이하는 일반적인 과정에 대해 살펴봤습니다. 각각의 문제에 대해 풀이해야 하는 방식이 다르기 때문에 뒤에서 여러 예시들을 보여드리겠습니다.

그 전에 한가지 내용에 대해 더 살펴볼 필요가 있습니다. 비제차 경계조건이 주어진 경우입니다. 선형조합의 원리는 경계조건이 제차를 따를 때만 사용 가능하기에, 비제차 경계조건이 주어진 경우에는 약간의 식 조작이 더 필요합니다.

다음 글에서는 이러한 내용에 대해 살펴보겠습니다.

감사합니다.