Contents
1. 대칭성을 갖는 함수 (Functions with Symmetry)
- 우함수, 기함수 등 대칭성을 갖는 함수를 살펴보겠습니다.
2. 대칭성을 갖는 함수의 푸리에 급수 (Fourier Series and Symmetry Function)
- 대칭성을 갖는 함수를 푸리에 급수로 어떻게 표현할 수 있는지 살펴보겠습니다.
3. 반구간 확장 (Half Range Expansion)
- 일정 구간에서 주기를 갖지 않는 함수를 푸리에 급수로 표현할 수 있습니다. 이는 주어진 구간에서의 함수를 주기를 갖는 우함수/기함수라고 가정을 함으로써 얻어낼 수 있는데, 이 방법에 대해 살펴보겠습니다.
1. 대칭성을 갖는 함수 (Functions with Symmetry)
1) 우함수와 기함수 (Even and Odd Function)
고등학교 시절에 수학과목을 공부하며, 우함수와 기함수를 배워볼 기회가 있었습니다. 간단하게 복습해보겠습니다.
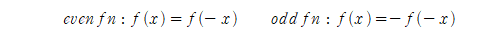
$x$ 대신 $-x$를 대입했을 때의 함숫값을 원래 함수와 비교할 수 있습니다. 이때 함숫값이 같다면, 이를 우함수(짝함수, even function)라고 합니다. 반대로 부호가 반대로 나온다면 이 함수를 기함수(홀함수, odd function)라고 합니다. 우함수는 $y$축에 대하여 대칭인 선대칭 함수의 한 종류이고, 기함수는 원점에 대해 대칭인 점대칭 함수의 한 종류입니다.
2) 선대칭과 점대칭 함수 (Line Symmetry and Point Symmetry Function)
우함수와 기함수를 확장할 수 있습니다. 즉, 어떤 임의의 선에 대한 함수가 있을 수 있고, 비슷하게 어떤 임의의 점에 대해 대칭인 함수도 얻을 수 있습니다. 이를 수학적으로 표현할 수 있습니다.
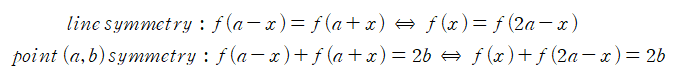
3) 함수 속에 숨겨진 대칭성 (Symmetry within arbitary function)
어떤 임의의 함수는 우함수와 기함수의 합으로 이루어져 있습니다. 그 이유는 다음과 같습니다.

어떤 함수를 우함수와 짝함수의 관계에 있는 함수들의 합으로 표현해도 그 결과가 동일합니다. 이를 이용해서 푸리에 급수를 대칭을 갖는 함수의 관점에서 살펴볼 수 있습니다.
2. 대칭성을 갖는 함수의 푸리에 급수 (Fourier Series and Symmetry Function)
이제 대칭성을 보이는 함수의 푸리에 급수를 살펴보겠습니다.
1) $[-\frac{T}{2},\frac{T}{2}]$에서 정의된 우함수의 푸리에 급수
푸리의 급수로부터 시작할 수 있습니다.
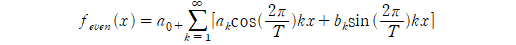
이때, 푸리에 계수를 결정하여 실제 우함수의 푸리에 급수를 얻을 수 있습니다. 각각의 계수를 구해보겠습니다. 이때 우함수/기함수에 대한 적분의 성질이 사용됩니다. 고등과정에서 배웠을 것이라고 생각하고, 바로 시작하겠습니다.
(1) $a_0$ 구하기

주어진 함수가 y축 대칭이므로, 주어진 구간에서의 적분은 0부터 시작하는 적분의 2배를 취한 것과 같음을 알 수 있습니다.
(2) $a_k$ 구하기
$a_0$를 구하는 것과 동일하게 $a_k$를 결정할 수 있습니다.
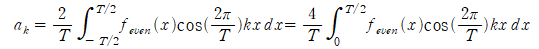
주어진 함수와 코사인함수 모두 우함수이므로, 이를 곱한 함수도 우함수입니다. 그렇기에 주어진 구간에 대한 적분을 0부터 시작하는 적분의 2배로 계산할 수 있습니다.
(3) $b_k$구하기
$b_k$도 함수의 대칭성을 이용한 적분의 계산을 이용하면 쉽게 구할 수 있습니다.
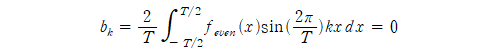
우함수와 기함수를 곱하면 기함수가 됩니다. 기함수에 대해서 대칭인 적분 구간에 대해 적분을 진행하면 적분 결과가 0인 것을 알고 있을 것입니다. 그러므로 $b_k = 0$입니다.
(1) ~ (3)을 통해서 우함수(짝수함수)에 대한 푸리에 급수를 얻을 수 있었고, 이를 정리하면 아래와 같습니다. 이처럼 얻는 푸리에 급수를 푸리에 코사인 급수 (Fourier Cosine Series)라고 합니다.
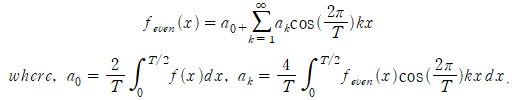
2) $[-\frac{T}{2},\frac{T}{2}]$에서 정의된 기함수의 푸리에 급수
우함수에서 했던 방법을 동일하게 따랐을 때, 대칭인 적분구간에서 정의된 기함수에 대한 푸리에 급수도 얻을 수 있습니다. 부가적인 설명을 생략하고 바로 푸리에 계수를 계산하겠습니다. 그 결과는 아래와 같습니다.

얻어진 푸리에 계수를 바탕으로 기함수(홀수함수)에 대한 푸리에 급수를 얻을 수 있고, 이를 아래에 정리해두었습니다.
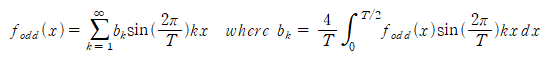
우리는 이를 푸리에 사인 급수 (Fourier Sine Series)라고 합니다.
3) 확장 : 제시된 함수를 푸리에 사인/코사인 급수를 이용해서 표현하기
앞서 모든 함수는 원점대칭인 함수와 y축 대칭인 함수의 합으로 구성되어 있음을 이야기 했습니다. 이 성질을 이용하면 주어진 함수의 푸리에 급수를 더 쉽게 구할 수 있습니다.
Step 1 주어진 함수를 원점대칭인 함수와 y축 대칭인 함수로 분리한다.
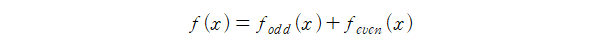
Step 2 원점대칭 함수에 대한 푸리에 사인 급수를, y축 대칭인 함수에 대한 푸리에 사인 급수를 구한다.

이때 푸리에 사인 급수와 코사인 급수에서 시그마의 index를 다르게 표현했는데, 이 둘을 합쳤을 때 혹시 결과가 다르게 나타날 수 있음을 예방한 것입니다. 같은 함수를 다른 과정을 거쳐 푸리에 급수로 표현하더라도 형태는 같아야 하기에 큰 문제는 없을 것이라고 생각됩니다. 하지만, 시그마를 여러개 사용할 때 함부로 index number를 같게 표현하는 것을 조심해야 함을 강조하고 싶었습니다. 일단, $l, k$를 교차해서 사용하더라도 큰 문제가 없다고 생각하겠습니다.
Step 3 푸리에 사인 급수와 푸리에 코사인 더하여 원래 함수의 푸리에 급수를 구한다.
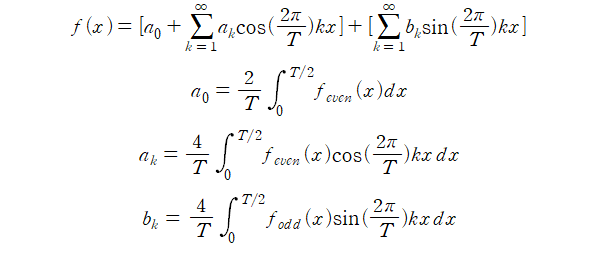
푸리에 계수를 계산할 때 원래 함수가 아닌 우리가 분리한 우함수/기함수를 기준으로 해야 함을 주의해야 합니다.
이러한 의문이 들 수 있습니다. 그냥 바로 푸리에 급수를 구해도 무방할텐데, 왜 우리는 대칭성을 이용한 절차를 거쳐야 하는가? 이는 푸리에 급수를 구함에 있어 더 편함을 보장하기 위함입니다. 예를 들어 주어진 함수가 $f(x)=x+1$이라면 $y=x$에 대한 푸리에 사인 급수를 구하고 $ y=x$에 대해 푸리에 코사인 급수를 구해서 더하는 것이 바로 푸리에 급수를 구하는 것보다 더 편할 것입이다.
3. 반구간 확장 (Half Range Expansion)
푸리에 사인/코사인 급수를 이용하면, 주기성을 갖고 있지 않은 함수이더라도 푸리에 급수를 구할 수 있게됩니다. 이처럼, 반구간($[0,a]$)에 대해 정의된 함수에 주기성/대칭성 등을 고려하여 푸리에 급수를 구하는 것을 반구간 확장(Half Range Expansion)이라고 합니다.
대략적인 반구간 확장의 알고리즘은 다음과 같습니다.
Step 1 주어진 함수를 우함수/기함수가 되도록 확장합니다.
Step 2 해당 우함수/기함수가 일정 주기를 갖고 반복된다고 가정합니다. 그리고 이에 대한 푸리에 급수를 얻습니다.
반구간 $[0,T]$에서 정의된 어떠한 함수$f(x)$를 우함수 및 기함수로 확장하는 반구간 확장을 보여드리고자합니다.
1) 우함수를 이용한 반구간 확장 (Half Range Expansion with Even Function)
Step 1 주어진 함수를 우함수가 되도록 확장합니다. 이를 위해서 반대편 반구간 $[-T,0]$에 새롭게 함수를 정의해야 하고, 이는 수학적으로 다음과 같이 표현할 수 있을 것입니다.
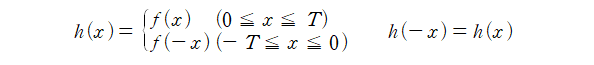
즉, $h(x)$는 원래 반구간에서 정의된 함수 $f(x)$를 y축 대칭하여 확장한 함수입니다.
Step 2 새롭게 얻은 함수 $h(x)$는 $2T$의 주기를 갖는 주기함수라고 가정하겠습니다. (그래야 y축 대칭인 성질을 그대로 이용할 수 있기 때문입니다.) 우함수에 대해 푸리에 급수를 구하는 것이기에 푸리에 코사인 급수를 구하면 될 것입니다.



결국 확장된 함수에서 원래 정의된 구간에 대해 함수를 얻으면 주기가 있다고 생각하고 얻은 푸리에 급수와 그 결과가 동일하게 나타나는 것을 알 수 있습니다.
2) 기함수를 이용한 반구간 확장 (Half Range Expansion with Odd Function)
우함수를 이용했던 것과 동일한 과정을 거치면 반구간확장을 할 수 있습니다. 간단하게 살펴보겠습니다.
Step 1 주어진 함수를 기함수가 되도록 확장합니다. 이는 반대편 반구간에 원점대칭한 함수를 확장한 형태일 것입니다.

Step 2 $g(x)$의 주기가 $2T$라고 했을 때, 이 함수는 원점대칭이므로 푸리에 사인 급수를 얻을 수 있습니다.

'전공 개념.zip > 편미분방정식 (PDE's)' 카테고리의 다른 글
| 5. 푸리에 적분 (Fourier Integral) (1) | 2022.05.04 |
|---|---|
| 4. 복소수 형태로 표현한 푸리에 급수 (Complex Form of Fourier Series) (0) | 2022.05.03 |
| 2. 푸리에 급수 (Fourier Series) (0) | 2022.04.30 |
| 1. 푸리에 급수 개괄 및 삼각함수의 특성 (Introduction to Fourier Series and Properties of Trigonometric Function) (0) | 2022.04.30 |
| 0. 편미분방정식을 시작하며.. (0) | 2022.04.30 |