화공노트: 화학공학 살펴보기

Contents Preview

타원형 편미분방정식의 2번째 예시입니다. 2차원에서의 열전도, 그 중에서도 한 방향으로 매우 긴 평면에서의 열전도에 대해 다루어보겠습니다.

2차원 타원형 편미분방정식 (1) 매우 긴 평면에서의 열전도 (2D Elliptic PDE: Conduction on Infinitely Long Thin Plane)

문제 상황은 다음과 같습니다.

$y$ 방향으로 매우 긴 평면에서 어떻게 전도가 일어나는지 살펴보는 문제입니다.

우선 경계조건을 살펴보겠습니다. $x$ 방향에 대한 경계조건은 제차의 형태를 따르고 $y$ 방향에 대한 경계조건은 비제차인 것으로 보입니다. 그렇기에 $x$ 방향에 대해 고유함수를 구하고, 나중에 $y$ 방향에 경계조건으로 고유함수의 계수를 결정지으면 될 것 같습니다.

변수분리법으로 문제 풀이를 시작하겠습니다.

Step 1 변수분리법을 위한 변수의 분리

온도가 각각 $x$와 $y$의 조합으로 표현될 수 있다고 생각하고 식을 다시 정리할 수 있습니다. $x$와 $y$에 관한 식을 얻을 수 있는데 이는 둘 다 일정해야 합니다. 경계조건도 다시 작성됩니다.

우리가 원하는 것은 자명하지 않은 해(nontrivial solution)입니다. 값이 0으로 나타나는 해 또는 조건을 원하지 않습니다. 이를 이용해서 각 변수에 대해 조건을 다시 작성했습니다.

Step 2 고윳값$\lambda$과 고유함수 찾기

2개의 상미분방정식에 대해 자명하지 않은 해가 존재하기 위한 고윳값을 찾아야 합니다. 이를 위해 고윳값의 부호마다 해가 존재할 수 있는지 살펴봐야 합니다.

이때 x에 대해 고윳값을 결정하고 고유함수를 찾을 것입니다. 왜냐하면 y는 비체자 경계조건을 갖고 있기 때문입니다.

X에 대한 식은 2차 선형 상미분방정식이며, 이는 특성방정식(characteristic equation)을 이용해서 풀이할 수 있습니다.

고윳값이 양수일 때부터 살펴보겠습니다.

(1) 고윳값이 양수일 때 $\lambda > 0$

경계조건을 편하게 적용하기 쉽게 쌍곡선함수(Hyperbolic Function)를 이용해서 식을 정리했습니다. 실제로 조건을 대입해본 결과 두 계수 A, B가 모두 0이 되며 이는 0만 해가 될 수 있음을 의미합니다. 따라서 고윳값이 양수일 때는 자명한 해(trivial solution)밖에 얻지 못하므로 다른 경우를 생각해야 합니다.

(2) 고윳값이 0일 때 $\lambda = 0$

고윳값이 0으로 중근을 가지면, 라그랑쥐의 차수축소법(Reduction of Order)을 사용해서 새로운 해를 얻을 수 있습니다. 여기에 경계조건을 적용하면 계수 A, B가 모두 0입니다. 따라서 이 경우도 우리가 원하는 고윳값이 될 수 없음을 알게됩니다.

(3) 고윳값이 음수일 때 $\lambda < 0$

해를 얻고 오일러 항등식(Euler’s Identity)을 이용해서 삼각함수로 해를 다시 작성한 것입니다. 경계조건을 대입해봤을 때 코사인함수에 대한 계수는 0이지만, 사인함수는 그 자체로 0이 될 수 있으므로 자명하지 않은 해를 얻을 수 있습니다.

사인함수가 0이 될 수 있는 상황을 생각해서 풀이하면, 이 스트름-리우빌 문제에 대한 고윳값과 고유함수를 얻을 수 있습니다.

Step 3 $Y(y)$ 결정하기

Step 2에서 찾은 고윳값을 이용해서 $y$에 대한 고유함수도 얻을 수 있습니다.

모든 경계조건을 적용할 필요는 없습니다. 결국 마지막에 고유함수에 대한 계수를 결정할 때 사용해야 하기 때문입니다. 다만 $y$가 무한대로 갈 때의 경계조건이 0, 즉 수렴하기 위해서는 계수 $C$가 0이 되어야 하며, 이를 반영해서 고유함수를 얻을 수 있습니다.

Step 4 각 변수에 대한 해의 조합

문제를 통해 $x, y$에 대한 해를 얻었으므로, 원래의 해를 찾기 위해 다시 조합할 수 있습니다. 하지만 고유함수에 대한 조합은 특정 $n$에 대한 해이므로, 일반화된 해를 찾기 위해 시그마를 취해줍니다.

이제 마지막 단계로 다가갑니다. 과연 고유함수에 대한 계수를 어떻게 정의해야 하는지에 대해서 말이죠.

이는 남은 경계조건의 사용, 그리고 내적으로 보이는 고유함수의 직교성을 활용해서 얻을 수 있습니다.

Step 5 고유함수의 계수 $E _n$결정

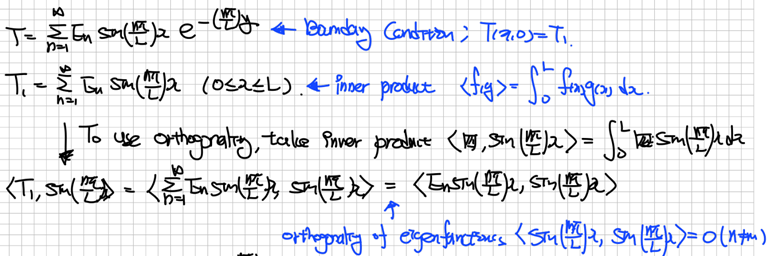
문제를 구하기 위해 사용하지 않은 경계조건을 활용합니다. 그리고 식을 정리하기 위해 내적을 취합니다. 고유함수의 직교성 때문에 자기 자신에 대한 내적을 제외한 항들은 모두 0으로 소거된 결과를 얻을 수 있습니다. 이를 정리하면 다음과 같습니다.

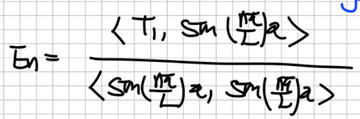
이제 분수, 분모를 계산해서 계수를 구체화할 수 있습니다.

특별할 것 없는 계산이지만, 코사인함수에 대한 식이 n에 따라 특정 값을 따르는 것을 이용해서 식을 단순하게 만들 수 있습니다.

삼각함수의 반각공식으로 알려진 관계를 이용하면 식을 정리할 수 있습니다.

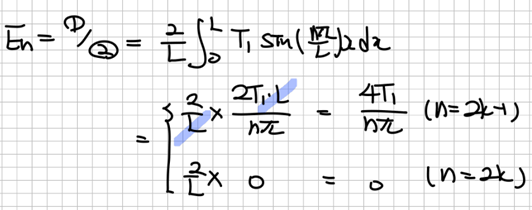
Step 7 해의 결정

각각에 대한 고유함수, 그리고 해를 알게 되었으므로 문제에서 구하라는 $x, y$에 대한 온도 분포를 알 수 있게 되었습니다. 계산 결과는 아래와 같습니다.

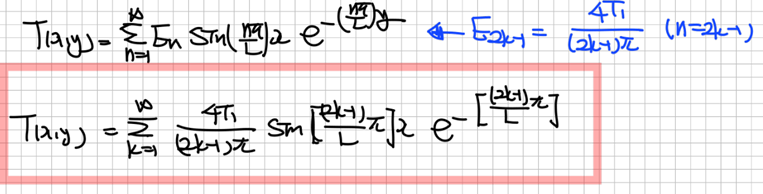
타원형 편미분방정식의 두 번째 예제인 매우 긴 평면에서의 열전도를 살펴봤습니다. 다음 예제는 크기가 정해져 있는 평면에서의 열 전도의 결과로 어떠한 온도 분포가 나오는지를 살펴보도록 하겠습니다.

감사합니다.

Contents Preview

이제부터 편미분방정식을 본격적으로 풀이하게 됩니다. 사실 변수분리법(Separation of Variables)을 이용해서 상미분방정식 문제로 바꿔주는 원리는 동일합니다. 다만 설정된 경계조건의 형태에 따라 문제를 풀이하는 과정이 다양할 뿐입니다. 그렇기에 여러 문제를 풀어보는 것이 중요합니다. 타원형 쌍곡선을 풀이하는 것은 라플라스 방정식(Laplace Equation)을 풀이하는 것이며, 3가지 예제를 가져왔습니다. 이 방정식 풀이의 이해에 도움이 되었으면 합니다. 이번 글에서는 1차 열전도를 살펴볼 것입니다.

1차 타원형 편미분방정식 (1D Elliptic PDE)

문제 상황은 다음과 같습니다.

1차원, 즉 x 방향으로의 전달만 고려하는 문제입니다. 1차 라플라스 방정식은 상미분방정식의 형태를 따르므로 일반해를 구하고, 주어진 경계조건으로 적분상수만 결정해주면 됩니다.

문제에서 요구하는 답을 구할 수 있고, 어떤 선형함수를 따라 온도가 바뀌는 것을 알 수 있습니다.

Contents Preview

공학수학에서 편미분방정식을 풀이할 때 경계조건이 제차(Homogeneous)인 경우를 많이 제시해줍니다. 어떤 경우에는 비제차 경계조건(Inhomogeneous Boundary Condition)이 제시된 경우도 많습니다. 이때는 고유함수의 선형조합으로 일반해를 나타내지 못합니다. 따라서 이번 글에서는 비제차 경계조건이 제시되었을 때 이를 해결하는 방법에 대해 살펴볼 것입니다. 이 방법을 경계조건의 제차화(Homogenization of Boundary Condition)라고 말하기도 합니다.

비제차 경계조건 문제는 다음과 같습니다.

어떤 일반화된 경계조건에 대해 그 결과가 0이 아님을 확인할 수 있습니다. 그렇기에 이 상황에서 우리가 문제를 풀이한다 하더라도 일반해를 얻을 수 없습니다.

해의 형태를 아래처럼 가정했을 때, 경계조건을 제차 형태를 따르도록 만들 수 있습니다.

원래 방정식의 해가 제차형태일 때의 해와 어떤 steady-state(equilibrium) 즉, 시간을 따르지 않는 해의 조합으로 쓰인다고 생각한 것입니다. 비제차 2차 선형 상미분방정식을 풀이하기 위해 우선 제차일 때의 해를 구하고, 그 다음 특수해를 구했던 것과 거의 유사한 것을 알 수 있습니다.

이제 이를 원래의 방정식에 대입해서 정리해보겠습니다.

어떤 평형상태(steady-state)에 대한 해를 구하고, 이를 제거하면 제차 형태를 따르는 경계조건을 구할 수 있게 됩니다.

지금까지 편미분방정식의 종류 및 판단방법, 변수분리법, 그리고 비제차 경계조건을 갖는 문제에 대한 해결방법까지 살펴봤습니다. 다음 글 부터는 각각의 편미분방정식을 어떻게 풀이해야 하는지 그 과정에 대해 자세하게 다루어보려고 합니다.

감사합니다.

Contents Preview

상미분방정식을 설명하는 많은 일반해들이 있습니다. 편미분방정식은 그렇지 않습니다. 아직 잘 설명된 일반해는 없고, 단지 알려진 풀이 방법만 존재할 뿐입니다. 편미방을 풀이할 수 있는 몇가지 방법이 있습니다. 공학수학을 배울 때는 변수분리법(Separation of Variables)을 처음 접하게 되기에, 이를 이용해서 편미방을 푸는 방법에 대해 살펴보겠습니다.

읽기 전에 보면 좋은 글

12. 스트룸 리우빌 이론(Strum-Liouville Theory) 예제: 푸리에 사인 급수 :: 화공노트: 화학공학 살펴보기 (tistory.com)

6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 :: 화공노트: 화학공학 살펴보기 (tistory.com)

변수분리법을 이용한 편미분방정식의 풀이

1) 의의

우리는 왜 변수분리법을 사용하게 되었을까요? 이를 이용하면 n차원 편미분방정식을 n개의 상미분방정식의 풀이로 문제상황을 바꿀 수 있습니다.

2) 적용

3차원 라플라스 방정식을 예로 들어보겠습니다. 3차원 편미분방정식이므로 아마 3개의 상미분방정식 풀이로 바뀔 것입니다.

풀이 과정을 단계별로 살펴보겠습니다

Step 1 종속변수에 관여한 변수들을 분리한다.

해가 각 변수에 대한 함수의 조합이라고 생각하는 것에서 풀이를 시작합니다. 저희는 현재 3차원 라플라스 방정식을 다루고 있기에 $x, y, z$ 3가지 변수가 관여할 것입니다. 그렇기에 위처럼 변수를 분리할 수 있습니다.

Step 2 식의 재작성

식 (**)를 식 (*)에 대입해서 정리할 수 있습니다.

$X, Y, Z$ 중 하나라도 0이 되면 해도 0이 되므로, $XYZ$는 0이 될 수 없습니다. 이를 이용해서 식을 정리한 것입니다.

Step 3 가정을 통한 상미분방정식으로의 문제 전환

식 (***)의 각 항들은 모두 일정한 값을 가져야 합니다. 이 이유에 대해 설명하겠습니다.

편미방의 해가 각각 독립적인 변수에 대한 함수의 조합으로 표현된다 생각하고 문제를 풀이하고 있습니다. 만약 이 세 개의 항 중 하나라도 상수가 아니라면, 하나의 변화로 인해 나머지 항들의 값도 따라 변하게 됩니다. 세 항의 합이 일정하기 때문입니다. 즉, 이 세 항 중 하나의 항이라도 일정하지 않다면, 독립적인 변수에 대해 식을 설정한 전제에 대해 모순이 발생하게 됩니다. 따라서 각각의 항들은 모두 일정한 값을 따라야 합니다.

각 항들을 일정한 상수로 두고 문제풀이를 이어가겠습니다.

위의 과정을 따라 식을 정리할 수 있습니다. 지금은 어떤 음수로 일정할 것이라고 가정했지만, 주어진 경계조건에 따라 다른 부호의 값을 따르는 경우도 있습니다. 원래는 그냥 어떤 상수로 일정하다고 두면 되겠습니다.

정리하자면, 변수분리법을 통해 식을 정리하면 3차원 편미분방정식이 3개의 상미분방정식을 풀이하는 문제로 바뀐 것을 알 수 있습니다.

Step 4 상미분방정식의 풀이와 해의 조합

현재 풀어야 하는 미분방정식은 선형 제차 상미분방정식이기 때문에 특성방정식(characteristic equation)을 풀이하면 해를 쉽게 얻을 수 있습니다.

A를 X, Y, Z를 대표하는 변수로 두었기에 각 변수에 대한 해도 표현할 수 있습니다.

각 변수에 대한 해를 얻었으니, 이들을 다시 곱하면 원래 해를 얻을 수 있습니다.

Step 5 선형결합을 통한 방정식의 해 구하기

우리가 위에서 얻은 해는 특정 고윳값에 대한 고유함수입니다. 이 편미분방정식이 선형이고, 주어진 경계조건이 모두 제차(homogeneous)라면 선형조합을 통해 주어진 구간을 설명할 수 있는 해를 구할 수 있습니다.

Step 6 계수의 결정

위에서 얻은 해는 모든 경계/초기조건이 결정되지 않은 해입니다. 그렇기에 주어진 초기/경계조건을 활용해서 고유함수의 계수를 결정해야 합니다.

이는 고유함수의 직교성을 이용해서 구하게 되며, 이를 위해 내적을 활용합니다. 주어진 조건들에 따라 계수가 다르게 결정될 것이고, 주어진 문제를 설명할 수 있는 특정해를 얻게 됩니다.

지금까지 변수분리법을 활용해서 편미분방정식을 풀이하는 일반적인 과정에 대해 살펴봤습니다. 각각의 문제에 대해 풀이해야 하는 방식이 다르기 때문에 뒤에서 여러 예시들을 보여드리겠습니다.

그 전에 한가지 내용에 대해 더 살펴볼 필요가 있습니다. 비제차 경계조건이 주어진 경우입니다. 선형조합의 원리는 경계조건이 제차를 따를 때만 사용 가능하기에, 비제차 경계조건이 주어진 경우에는 약간의 식 조작이 더 필요합니다.

다음 글에서는 이러한 내용에 대해 살펴보겠습니다.

감사합니다.

Contents Preview

안녕하세요 화공노트입니다. 지금까지 편미분방정식 풀이를 위해 필요한 개념 2가지(푸리에 급수, 스트룸 리우빌 문제)에 대해 살펴봤습니다. 드디어 편미분방정식 공부를 위한 준비를 마쳤습니다.

이번 글에서는 우리가 주로 다룰 편미분방정식의 형태와 종류, 그리고 이를 분류하는 방법에 대해 살펴볼 것입니다. 편미분방정식은 상미분방정식과 달리 조건 설정이 매우 유의미합니다. 그렇기에 편미분방정식에서의 조건 설정과 조건이 갖는 의미에 대해서도 살펴보겠습니다.

1. 편미분방정식의 형태 (Formation of Partial Differential Equation)

편미분방정식은 상미분방정식과 달리 서로 다른 2개 이상의 변수를 포함하고 있습니다. 대부분 시간-공간 변수들이 관여합니다. 이해를 돕기 위해 선형 2차 편미분방정식(linear second order partial differential equations)을 살펴보겠습니다.

1) 미분 횟수 고려

종속변수 $u$에 대해 앞의 세 항은 2번 미분되었고, 뒤의 세 항은 1번 미분됨을 알 수 있습니다.

2) 제차, 비제차

한편, 등호 오른쪽에 있는 항 $g$의 형태가 이 편미방의 제차, 비제차 여부를 결정합니다. 만약 $g$가 0이라면 이 방정식은 제차(homogeneous)이며, 0이 아니라면 비제차(inhomogeneous)임을 알 수 있습니다.

2. 편미분방정식의 분류와 예시 (Classification of PDE and Examples)

1) 편미분방정식의 분류

어떤 편미분방정식의 문제가 주어졌을 때, 이 방정식의 형태를 구분하는 것이 중요합니다. 2차 미분항(2nd Differential Terms)의 계수관계를 이용하면 주어진 방정식의 종류를 판단할 수 있습니다.

이 식은 이차방정식에서 판별식하고 매우 형태가 유사합니다. 이 식의 부호에 따라 방정식의 종류를 구분할 수 있습니다. 음수라면 타원형 편미분방정식(Elliptic PDE), 양수라면 쌍곡선형 편미분방정식(Hyperbolic PDE), 그리고 0이라면 포물선형 편미분방정식(Parabolic PDE)이라고 합니다.

2) 편미분방정식의 예시

각 종류의 편미분방정식에 대표적인 예시를 살펴보겠습니다

(1) 쌍곡선형 편미분방정식 ($b^2-4ac>0$)

양자역학에서 주로 등장하는 파동방정식(Wave Equation)은 쌍곡선형의 대표 예시라 할 수 있습니다.

(2) 포물선형 편미분방정식 ($b^2-4ac=0$)

열 및 물질전달에서 분자 사이의 접촉으로 인해 물질, 열, 에너지 등이 전달되는 내용을 배울 수 있습니다. 이를 설명하는 열 전도 방정식(또는 확산 방정식, Heat/Diffusion Equation)은 포물선형의 대표적인 예시라 할 수 있습니다.

(3) 타원형 편미분방정식 ($b^2-4ac<0$)

한편, 라플라스 방정식(또는 포텐셜 방정식, Laplace/Potential Equation)은 타원형 편미분방식을 대표하는 예시입니다.

3. 편미분방정식의 풀이를 위한 조건 설정 (Setting Condition for Solving PDE)

1) 편미분방정식의 해의 특성

편미분방정식을 풀이하면 해의 다양성을 확인할 수 있습니다. 같은 방정식으로부터 시작하더라도 경계조건과 경계조건에 의해 최종 형태는 상이합니다.

많은 공학관련 전공을 공부할 때, 현상을 일반적으로 설명하는 방정식들을 유도할 때가 있습니다. 이 식에 문제 상황을 나타내는 조건을 설정하고 풀이할 때 해를 얻을 수 있습니다. 즉, 여러분은 정량적인 예측을 하기 위해 식을 유도하고 풀이하게 되는 것이지요.

2) 풀이를 위해 필요한 조건의 개수

편미분방정식을 풀이하기 위해 조건을 적절히 설정해주어야 합니다. 시간과 관련된, 그리고 공간과 관련된 변수에 대해 설정해야 하는 조건, 그리고 그 개수는 다음과 같습니다.

(1) 시간변수와 관련된 항은 초기조건(Initial Condition, IC)을 설정하고, 공간변수와 관련된 항은 경계조건(Boundary Condition)을 설정한다.

(2) 각 변수에 대해 미분 차수만큼 조건이 필요하다.

파동방정식을 예로 들어 조건 설정의 이해를 돕고자 합니다

시간과 관련된 항에 대해서는 초기 조건을, 공간과 관련된 항에는 경계 조건을 각각 2개씩 설정해야 함을 알 수 있습니다. 둘 다 미분이 2번씩 되어있기 때문입니다. 조건과 관련된 내용이 더 궁금하다면 아래의 글이 도움이 될 것입니다.

3) 경계조건의 물리적 의미

경계조건은 초기조건의 또 다른 형태입니다. 하지만 경계조건은 몇 가지 물리적 의미를 포함하고 있습니다.

(1) 경계조건은 어떤 시스템의 양 끝 정보만 표현하지만, 이를 이용해서 해를 결정하면 분석하고자 하는 시스템의 물성의 분포를 알 수 있도록 도와줍니다.

(2) 그렇기에 실험 분석 시 편미분방정식을 활용해야 할 때, 시스템 내부의 정보를 알기 위해서 올바른 경계조건만 설정해주면 됩니다.

Contents Review

지금까지 편미분방정식의 형태와 종류를 알아보고, 어떤 종류인지 분류하는 방법을 살펴봤습니다. 그리고 이를 풀이하기 위해 조건을 설정하는 방법에 대해서도 살펴봤습니다.

다음 글에서는 편미분방정식을 풀이할 때 가장 많이 사용하게 될 변수분리법(Separation of Variables)에 대해 살펴보겠습니다.

글에 관해 궁금한 점이 있으면 댓글 남겨주세요.

감사합니다.

Contents Preview

지금까지 스트룸 리우빌 이론이 무엇인지, 스트룸 리우빌 연산자가 어떤 특성을 갖고 있는지 살펴봤습니다. 이번 글에서는 스트룸 리우빌 이론의 가장 단순한 예제를 같이 살펴보며, 실제 상미분방정식을 풀이하는 데 스트룸 리우빌 이론이 어떻게 이용될 수 있는지 살펴보겠습니다.

스트룸 리우빌 이론을 이해하기 위해 간단한 예시를 살펴보겠습니다.

어떠한 이차 상미분 방정식은 스트룸 리우빌 연산자를 이용해서 작성될 수 있었습니다. 실제로 그런지 살펴보겠습니다.

스트룸 리우빌 연산자에서 $p, q, r$이 각각 $-1, 0, 1$이 될 때 예시로 가져온 미분연산자가 될 수 있음을 확인할 수 있습니다. 그렇기에 주어진 미분방정식을 고윳값 문제로 해석할 수 있습니다.

첫번째 등호 관계는 주어진 미분연산자를 취한 형태를 표현한 것이고, 두 번째 등호는 미분연산자에 대해 고윳값 문제를 나타낸 것입니다. 이제 문제를 풀기 위해 두 등호 사이의 관계를 얻을 수 있습니다. 그 결과 주어진 문제를 2차 선형 상미분방정식으로 해결할 수 있음을 알게 됩니다.

결국, 미분방정식을 풀이해서 고윳값(eigenvalue)을 얻을 수 있고, 이때 얻은 해는 고유함수(eigenfunction)라고 말할 수 있습니다.

2차 선형 상미분방정식은 특성방정식(characteristic equation)을 이용해서 풀이합니다. 이 문제의 경우 고윳값의 부호가 상미분방정식의 해의 형태를 결정합니다. 각 고윳값의 부호에 따라 상미분방정식의 해가 어떻게 나타나는지 살펴보겠습니다.

특성방정식의 풀이는 결국 이차방정식의 풀이로부터 시작됩니다. 그렇기에 고윳값의 부호에 따라 얻어지는 근의 개수 및 형태가 다르며, 이를 정리할 수 있습니다. 고윳값이 양수일 때는 포물선 함수(Hyperbolic Function)을, 고윳값이 음수일 때는 오일러 항등성(Euler’s Identity), 그리고 고윳값이 0인 중근을 가질 때에는 라그랑쥐의 차수 축소법(Reduction of Order)을 이용했습니다. 결과를 다시 요약하겠습니다.

한편, 조건을 만족하는 해를 얻기 위해 경계조건을 대입해봐야 합니다. 이를 위해 일반해에 경계조건을 대입해서 자명하지 않은 해(nontrivial solution)를 얻어야 합니다. 이때 자명하지 않은 해란 조건을 만족하는 해가 0이 아닌 어떠한 해를 의미합니다. 직접 대입해보며 살펴보겠습니다.

고윳값이 0 이상인 경우, 주어진 경계조건을 만족하기 위해서는 계수가 모두 0이 되어 해도 0이 됩니다. 이는 우리가 미분방정식을 풀지 않아도 얻을 수 있는 자명한 해입니다. 그렇기에 이 경우는 주어진 문제의 답이 될 수 없습니다. 정확히는 크게 의미 있는 정보를 주지 않습니다.

고윳값이 음수인 경우는 조금 다른 양상을 보입니다. 경계조건을 만족시키는 어떠한 고유함수가 존재할 수 있으며, 이는 고윳값의 결정으로 정해지게 될 것입니다.

고유함수의 직교성을 이용한다면, 경계조건을 만족하는 어떤 함수를 고유함수의 선형조합으로 표현할 수 있다는 사실을 배웠습니다. (Eigenfunction Expansion) 이를 나타내면 다음과 같습니다.

주어진 문제에 대한 고유함수를 선형조합으로 표현했더니 푸리에 사인 급수(Fourier Sine Series)임을 알게 되었기에, 각 고유함수에 대한 계수를 구하는 것은 어렵지 않을 것입니다.

Contents Preview

에르미트 연산자에 대한 고윳값 문제를 풀면, 서로 직교하는 고유함수들을 얻을 수 있습니다. 스트룸-리우빌 연산자도 동일한 특성을 갖고 있습니다. 이를 증명하고 직교성을 이용해서 어떤 구간 내의 함수를 고유함수의 선형조합으로 표현하는 방버에 대해 살펴보겠습니다.

고윳값 문제를 해결하면 고윳값과 이에 해당하는 고유함수를 구할 수 있습니다. 연산자의 종류에 따라 고유함수의 특성이 달라지는데, 에르미트 연산자에 대한 해는 서로 직교하는 특성이 있습니다. 앞서 스트룸-리우빌 연산자의 자기수반성 증명을 통해 이 연산자도 에르미트 연산자로 생각할 수 있으며, 그렇기에 스트룸-리우빌 연산자의 해도 서로 직교할 것이라고 예상할 수 있습니다. 이를 간단하게, 그리고 실제 내적을 통해 식을 조정해보면서 증명해보도록 하겠습니다.

<증명 1> 고윳값 문제를 이용한 고유함수의 직교성 증명

서로 다른 두 고윳값에 대해, 그리고 고유함수에 대해 생각해보겠습니다. 연산자의 자기수반성을 이용해서 식을 표현했습니다. 고윳값-고유함수 관계를 이용해서 식을 마저 전개해보겠습니다.

두 고윳값은 서로 다르기에 내적의 결과가 0이 되어야 합니다. 이는 결국 두 고유함수가 서로 직교함을 의미합니다.

위의 증명은 고윳값 문제 관계를 이용해서 고유함수의 직교성을 증명한 것입니다. 내적을 전개하고, 식을 변형해보면서 직교성을 다시 한 번 증명해보도록 하겠습니다.

<증명 2> 내적을 전개, 변형해서 보이는 고유함수의 직교성

어떤 두 함수가 직교한다면, 내적의 결과는 0일 것입니다. 우선 고윳값 $\lambda$에 대한 고유함수를 이용해서 식을 변형해보겠습니다.

의 식을 내적 형태로 바꾸기 위해 식을 변형하겠습니다.

처음 시작을 $\lambda$에 대한 고유함수로부터 내적을 표현했습니다. $\mu$에 대한 고유함수로부터도 식을 전개할 수 있으며, 이를 나타내면 다음과 같습니다.

두 내적 사이의 관계를 표현하기 위해서 (*)과 (**)의 차이를 구해보겠습니다.

스트룸-리우빌 연산자의 자기수반성을 증명할 때와 비슷한 결과를 얻을 수 있습니다. 어떤 특정 수치는 결국 경계 조건에 의해서 소거되고, 그래야 내적의 결과가 0인 것을 얻을 수 있습니다. 경계조건의 대입을 통한 항의 처리는 생략하고, 증명을 마무리해보겠습니다.

<증명 1>과 결국 내용이 비슷합니다. 서로 다른 고윳값의 차가 0이 될 수 없으니 반드기 고유함수 사이의 내적이 0이 되어야 하는 것을 알 수 있습니다. 이는 두 고유함수가 서로 직교한다는 것을 뜻합니다.

한편, 고유함수의 직교성을 이용하면 경계조건을 만족하는 함수를 고유함수의 선형조합으로 표현할 수 있습니다.

고유함수의 선형조합으로 경계조건을 만족하는 함수를 표현할 수 있고, 내적을 이용해서 고유함수의 계수를 결정할 수 있습니다. 이 특성을 증명해보겠습니다.

어떤 함수를 고유함수의 내적으로 표현했을 때, 내적을 통해서 특정 계수만을 남길 수 있습니다. 그렇기에 함수를 스트룸-리우빌 연산자에 대한 고유함수들의 조합으로 표현할 수 있습니다.

아마 공학수학 또는 수리물리학을 공부한 분들이라면 위의 식과 유사한 형태를 푸리에 급수에서 살펴볼 수 있었을 것입니다. 푸리에 급수도 가중치가 1인 내적을 이용한 고유함수의 조합을 이용한 것이기 때문입니다.

Contents Preview

스트룸-리우빌 연산자가 에르미트 연산자이기 때문에, 이 연산자의 성질을 공유할 것입니다. 그 중에서 에르미트 연산자의 고윳값 문제를 풀었을 때 얻은 고윳값은 항상 실수인 특성을 스트룸-리우빌 연산자에서도 동일하게 나타나는 것을 보일 것입니다.

스트룸-리우빌 연산자도 고윳값 문제로 생각할 수 있습니다. 이를 식으로 나타내면 아래와 같습니다. 

우리가 보이고자 하는 고윳값은 위의 관계에서 확인할 수 있습니다. 이 문제를 풀어서 얻은 고윳값이 실수라는 것을 뜻합니다, 이제 증명을 시작하겠습니다.

<증명>

스트룸-리우빌 연산자는 자기수반성을 갖고 있습니다. 이로부터 증명을 시작할 수 있습니다.

증명을 이어나가기 위해 내적을 표현해보겠습니다. 그리고 고윳값 문제 관계를 이용해서 식을 변형했습니다.

이와 비슷하게 오른쪽 항의 내적도 표현할 수 있습니다.

이제 두 내적 결과가 같음을 이용하여 관계성을 살펴보겠습니다.

같은 고유함수(eigenfunction)에 대한 내적 결과는 0이 될 수 없습니다. 그렇기에 고윳값과 그 켤레의 형태가 같아야만 자기수반성이 설명됩니다. 어떠한 값과 그의 켤례형태가 동일하다는 것은 해당 값이 실수(real)임을 의미합니다. 따라서 스트룸-리우빌 연산자에 대한 고윳값은 항상 실수인 것을 알 수 있습니다.

증명과는 별개의 이야기이지만, 어떠한 연산자의 고윳값이 실수인 사실은 물리에서 중요한 특성 중 하나입니다. 어떠한 함수의 연산자를 취하는 것은 특정 함수로부터 원하는 정보를 특정하여 관측하겠다는 것을 의미합니다. 실제 우리가 관측하는 정보들은 모두 실수인데, 만약 연산자의 결과가 허수라면 현상을 이해하는데 어려움이 생길 것입니다. 그렇기에 이용하고자 하는 연산자가 에르미트 연산자임을 알고 있다면 이를 관측에 적극적으로 사용할 수 있다는 이점이 있습니다.

Contents Preview

스트룸-리우빌 연산자가 자기수반성을 가짐을 보이며, 사실은 이 연산자가 에르미트 연산자(Hermitian Operator)임을 보일 것입니다.

스트룸-리우빌 연산자는 특정 공간 안에서 자기수반성을 갖습니다. 이를 증명하도록 하겠습니다.

<증명 1> 일반적인 경계조건에 대한 스트룸-리우빌 연산자의 자기수반성

본격적인 증명에 앞서 한가지를 살펴보겠습니다. 연산자를 각기 다른 함수에 취했을 때 그 내적 결과가 같을 때, 우리는 이 연산자가 자기수반성을 갖는다고 말할 수 있습니다. 하지만, 우리는 어떠한 연산자를 켤레화하고(Conjugation) 전치(Transpose)했을 때에도 기존의 연산자와 같을 때 자기수반성을 갖는다고 알고 있습니다. 내적을 이용해서 위처럼 증명을 시작해도 자기수반성임을 보일 수 있는지 살펴보겠습니다.

이처럼 켤레화를 했을 때 연산자의 위치가 변하고, 이를 이용하면 내적을 이용해서도 자기수반성을 표현할 수 있게 됩니다, 계속 증명을 이어나가겠습니다.

각각의 내적을 진행했고, 그 결과를 얻을 수 있었습니다. 식을 정리하기 위해서 부분적분법(Integrate by parts)를 이용한 것을 확인할 수 있습니다. 이제 이 둘 이 같아질 수 있음을 확인하기 위해 두 항을 빼보겠습니다.

만약 두 내적의 차가 0이였다면 우리는 바로 증명을 마칠 수 있었을 것입니다. 하지만 어떠한 값들의 조합이 결과로 나온 것을 확인할 수 있습니다. 이를 소거하기 위해서 우리는 경계조건(boundary condition)을 확인해야 합니다. 우선, 일반적인 제차의 경계조건(homogeneous Boundary Condition을 설정해보겠습니다.

그리고 이 경계조건을 켤례화할 수 있습니다. 켤례화를 한다고 하더라도 제차 형태의 식이므로 값에는 변동이 없을 것입니다.

주어진 조건, 그리고 켤례화한 조건을 변형하여 관계식을 얻을 수 있습니다.

이를 식 (*)에 대입하여 정리할 수 있고 그 결과는 다음과 같습니다.

<증명 2> 특수한 형태의 경계조건에 대한 스트룸-리우빌 연산자의 자기수반성

만약 경계조건의 계수가 0을 포함하고 있어 어떠한 유리식의 형태로 식을 정리할 수 없는 경우도 있을 것입니다. 이때에도 해당 증명은 성립하며, 각 조건에 대해 살펴보겠습니다.

(1) Dirichlet Boundary Condition

이 조건에서는 변화 정도를 표현하는 계수 d가 0입니다. 이를 이용해서 조건을 다시 쓸 수 있고, 식을 정리할 수 있습니다.

(2) Neumann Boundary Condition

이 조건에서는 상태를 표현하는 계수 c가 0입니다. 마찬가지로 조건을 다시 작성하고, 식을 정리하여 자기수반성을 보일 수 있습니다.

(3)  Periodic Boundary Conditon

한편, 주기성을 보이는 경계조건에 대해서도 자기수반성이 성립하는데, 이를 보이면 다음과 같습니다.

지금까지 스트룸-리우빌의 자기수반성 증명을 살펴보았습니다. 이 특성은 스트룸-리우빌 연산자는 자기수반성을 가지며, 이 연산자를 에르미트 연산자로 생각할 수 있음을 나타냅니다. 에르미트 연산자의 특성을 공유합니다. 다음 글들에서는  여러 특성들 중에서 중요한 특성 2가지에 대해 더 알아보도록 하겠습니다.

Contents

1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)

- 미분방정식을 풀이하는 데 있어 필요한 조건들에 대해 간략히 소개합니다. 초기 시점에 비중을 둔 초기조건과 공간에 비중을 둔 경계조건에 대해 설명을 드리고자 합니다. 주어진 미분방정식의 해를 특정하기 위해 필요한 조건의 개수에 대해 논의해보고, 물리학에서 경계조건의 중요성에 대해서도 말씀드리겠습니다.

2. 경계조건의 분류 (the Classification of Boundary Condition)

- 경계조건을 구분하는 것은 생각보다 중요한 일인데, 이러한 이유와 경계조건의 종류를 살펴보겠습니다. 

0. Introduction - 조건설정의 필요성 (the Necessity of Setting Conditions)

본격적인 내용에 들어가기 앞서 한가지 내용을 먼저 같이 생각해보려 합니다. 우리는 왜 미분방정식을 풀이하는 것에 대해 배워야 할 필요가 있을까요? 여러 이유를 들 수 있습니다. 제 생각에는 지배방정식(Governing Equation)을 풀이하기 위해 미분방정식을 공부해야 한다고 생각합니다. 

지배방정식은 어떠한 상황에서 알고 있는(또는 측정할 수 있는) 변수들과 우리가 알고 싶은(또는 측정해야 하는) 변수들 사이의 관계를 나타내는 식입니다. 이들은 특정 시점($t$)과 미소 시간이 흐른 시점($t+dt$) 사이의 물성 변화로부터 얻어지기 때문에 미분방정식의 형태를 띠는 경우가 많습니다. 수지 방정식(Balance Equation), fin에 대한 열전도 방정식(Heat Conduction) , 1D Box에 놓여있는 입자의 파동방정식(Wave Equation) 등을 예로 들 수 있습니다. 이러한 방정식들을 풀이해야 우리가 원하던 정량적인 정보를 얻을 수 있습니다. 그렇기에 학부수준의 문제를 해결하기 위해서는 미분방정식을 다룰 수 있어야 한다고 생각합니다. 

지배방정식들은 놓여있는 조건(상황)에 따라 그 해가 매우 상이합니다. 추후에 같이 살펴보겠지만, 같은 대류현상에 대한 지배방정식을 풀이하더라도 주변이 단열되어있는지, 아니면 일정하게 가열되고 있는지에 따라 편미분방정식의 형태는 매우 다르게 나타납니다. 따라서 우리는 지배방정식에 대한 조건을 올바르게 설정할 수 있어야 합니다.

조건은 크게 2가지로 분류됩니다. 관측시점을 중요시 하는 초기조건(Initial Condition)과 관측위치를 중요시 하는 경계조건(Boundary Condition)이 있습니다. 이제 조건에 대해 본격적으로 얘기해보겠습니다.

1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)

1) 초기조건 (Initial Condition)

초기조건은 어떠한 미분방정식에서 특정 시점에 대한 해의 정보들의 집합을 의미합니다. 초기조건은 시간에 대한 물성 변화를 설명할 때 사용되며, 물체 관측의 시작점($t=0$)에서의 정보를 표현하는 경우가 많습니다. 수식으로 표현하면 다음과 같습니다.

초기조건은 주로 상미분방정식, 또는 편미분방정식 중 시간과 관련된 정보를 결정하는 데 사용됩니다.  $n$차 상미분방정식을 결정하기 우해서는 $n$개의 초기조건이 필요합니다. 

2) 경계조건 (Boundary Condition)

경계조건은 특정 위치에 대한 해의 정보들의 집합을 의미합니다. 경계조건은 장소(위치)변화에 대한 물성을 표현할 때 사용합니다. 주로 검사체적(Control Volume, system)과 주변(Surrounding)을 구분짓는 경계표면(Control Surface)에 대한 정보들이 주로 나타납니다. 만약 물체가 1D에 놓여있다면 수직선 양 끝 정보가, 3D에 놓여있다면 체적의 표면들에 대한 정보가 표현되어 있을 것입니다. 1D Differential Equation에 대한 경계조건을 수식으로 표현하면 다음과 같습니다. 

한번 언급했듯, 편미분방정식의 해는 시공간에서의 물성의 분포를 표현합니다. 그렇기에 편미분방정식에서의 경계조건에 대한 중요성은 매우 높습니다. 

3) 해 결정을 위해 필요한 조건의 개수

적절한 종류의 조건을 사용하는 것도 중요하지만, 적합한 해를 찾기 위한 조건의 개수를 아는 것도 중요합니다. 조건의 개수를 너무 많이 부여하면 과적합한 해가 얻어지고, 부족한 개수의 조건을 설정할 경우 해가 정해지지 않습니다.

적합한 해의 개수를 결정하기 위해서는 미분된 변수의 종류와 최고 미분된 횟수를 고려하면 됩니다. 시간에 대한 미분의 차수와 공간에 대한 미분의 차수를 파악한 후 시간에 대한 미분에는 초기조건을 부여하고, 공간에 대한 미분에는 경계조건을 설정하면 됩니다. 예를 들어 보겠습니다.

어떤 편미분 방정식이 시간에 대해 1차 미분, 공간에 대해 2차 미분이 되어있다면 1개의 초기 조건과 2개의 경계조건이 필요합니다.

미분은 정보를 소거하는 연산이고, 적분은 정보를 확장하는 연산입니다. 미분방정식을 푼다는 것은 결국 적분을 거쳐 해를 얻는 것을 의미하기에, 미분된 횟수만큼 적분을 해주어야 합니다. 이는 미분된 횟수만큼의 조건을 필요로 한다는 것으로 해석할 수 있습니다.

예를 들어 보겠습니다.

이 미분방정식은 등가속도 운동을 표현하는 간단한 형태의 미분방정식입니다. 이를 풀이하는 과정은 아래와 같습니다.

미분방정식은 풀이했지만 아직 조건이 충분히 제시되지 않았습니다. 2계 상미분방정식의 풀이를 위해서 2번 적분한 것을 확인할 수 있을겁니다. $A_0$과 $B_0$이 결정되어야 우리가 원하던 특정한 해를 얻을 수 있는 것입니다. 2개의 적분상수가 결정되어야 하므로 2개의 조건이 필요합니다. 이 문제는 측정할 수 있는 시점에서의 수치를 기반으로 정보를 확장하는 것이므로 초기조건을 설정하여 해를 특정하겠습니다. 

이 결과 해는 다음과 같이 표현됩니다.

이 물리적 현상을 관통하는 지배방정식에 조건을 설정하여 풀이했더니 하나의 특정한 해를 얻은 것을 확인할 수 있었습니다. 

이 문제에 다른 조건을 설정해서 풀어보겠습니다. 이번에는 경계조건을 걸어보겠습니다. 편하게 논의하기 위해 공간과 관련된 항에 경계조건을 설정하라고 이야기했지만, 좀더 구체적인 경계조건의 표현은 아래와 같습니다.

"경계조건은 정의역의 양 끝 지점에서의 해와 관련된 정보를 제시한 것"

즉  경계조건은 외부의 영향을 직접적으로 받는 지점에서의 정보가 제시된 것임을 알 수 있습니다. 한번 살펴볼까요?

정의역이 $t\in[0,1]$일 때 경계조건이 다음과 같다고 생각해보겠습니다. 이를 해에 대입했을 때 적분상수를 계산할 수 있습니다.

이제 특정한 해를 표현하고 이용할 수 있습니다.

요약하자면 미분방정식의 해를 특정하기 위해서는 조건이 필요하고, 그 개수는 독립변수에 대한 최대 미분 횟수와 동일합니다. 

4) 물리학에서 경계조건의 중요성

경계조건은 물리학/공학에서 큰 중요도를 가집니다. 경계에 대한 정보를 갖고 지배방정식을 풀이할 수 있다면 정의된 영역에 대한 모든 정보를 예측할 수 있기 때문입니다. 예를 들어 2D Plate에 대한 문제를 해결해야 한다고 생각해봅시다. 그렇다면 각 변에서의 물성에 대한 정보만 알고 있으면, 2D Plate 전 영역에 대한 물성의 정보를 예측할 수 있다는 것을 의미합니다. 즉, 부분의 정보로부터 전체의 정보를 이끌어내는 것을 가능하게 해주는 것이 경계조건 입니다.

경계는 실험자에게도 유리한 지점입니다. 바로 측정이 가능한 위치이기 때문입니다. 당장 정육면체 내부의 온도 분포를 조사한다고 했을 때, 정육면체 중심보다는 각 면에다가 온도 조절 장치를 설치하는 것이 유리할 것입니다.

실험 설계 측면에서도, 해의 결정에 있어서도 경계조건은 중요한 것은 당연합니다.

2. 경계조건의 분류 (the Classification of Boundary Condition)

편미분방정식을 풀이할 때 유의해야 하는 점이 있습니다. 편미분방정식의 종류에 따라 특정한 해를 얻을 수 있는 경계조건의 형태가 정해져있습니다. 그렇기에 경계조건을 꼭 분류할 수 있어야 합니다. 특히 스투름-리우빌 문제를 풀이하는 데 필요한 경계조건을 일반화해서 표현할 수 있는데, 이는 다음과 같습니다.

이를 물리적으로 해석해볼 수 도 있겠습니다. $y(a)$는 경계에서의 물리량이 일정하다는 것을 의미합니다. 예를 들어 일정한 온더를 유지하는 열원(Heat Reservior)이 있을 수 있습니다. 반면에 $y'(a)$는 경계에서 물리량의 변화가 일정하다는 것을 의미합니다. 예를 들면 유체의 흐름(flux)가 경계표면에서 일정한 상황을 생각해볼 수 있습니다. 결국 경계조건은 물성에 대한 특정 값 또는 변화량을 포함하고 있을 수 있음을 시사합니다. 계수 $\alpha, \beta, m, n$의 유무에 따라 경계 조건의 종류가 달라집니다.

(1) Dirichlet BC

이 경계조건은 경계지점에서의 물리량들의 값이 제시된 조건을 의미합니다. 즉, 변화를 나타내는 값들의 계수인 $m, n$이 0이 되는 상황을 얘기하는 것입니다. 

(2) Neumann BC

이 경계조건은 경계지점에서의 도함수(또는 변화) 정도가 제시된 조건입니다. 즉, 일정한 값을 나타내는 항들의 계수인 $\alpha, \beta$가 0이 되는 상황을 뜻합니다.

(3) mixed Dirichlet-Neumann BC (or Cauchy BC)

이 경계조건은 특정 물리량과 물리량의 변화 정도가 모두 제시된 경계조건입니다.

(4) periodic BC

이 경계조건은 경계지점에서의 물리량이 동일하고, 해당 수치들이 주기적으로 나타나는 조건입니다. 예를 들면 다음과 같습니다.

한편, 위에서 조건들이 갖는 값 $A, B$가 모두 0이라면 이 조건은 제차(homogeneous)라고 하고, 그렇지 않다면 비제차(Inhomogeneous)라고 합니다. 제차 경계조건이 제시된 경우 해를 표현하기 편리하기 때문에 제체화를 할 수 있어야 합니다. 이는 추후 비제차 경계조건이 할당된 편미분방정식을 풀이할 때 같이 살펴보겠습니다.

스투름-리우빌 정리를 공부하다가 갑자기 경계조건에 대해 장황하게 이야기를 한 이유에 대해 궁금할 수 있다고 생각합니다. 이는 바로 다음 글에서 살펴볼 스투름-리우빌 미분방정식의 해의 직교성(Orthogonality)를 보일 때, 경계조건에 대한 논의가 필수적이기 때문입니다. 해당 내용을 다룰 때 다시 한번 설명하겠습니다.