
Contents
1. 1차 선형 상미분방정식의 형태 (Formula of the first order ODE)
2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)
- 제차 1차 선형 상미분방정식의 풀이
- 비제차 1차 선형 상미분방정식의 풀이
1. 1차 선형 상미분방정식의 형태 (Formula of first order ODE)
1차 선형 상미분방정식은 아래의 형태를 갖습니다.

종속변수가 총 미분된 횟수를 미분방정식에서의 차수라고 생각할 수 있습니다. 여기서는 y가 한번 미분되었다는 것을 나타내기 위해 ‘ 대신 (1)을 윗첨자로 사용했습니다. 마찬가지로 forcing function으로 사용된 q(t)가 0이면 이 미분방정식은 homogeneous ODE이며, 0이 아니라면 Inhomogeneous ODE입니다.
2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)
1) 제차 1차 선형 상미분방정식 (Homogeneous 1st order Linear ODE)
초기조건(IC)이 주어진 homogeneous ODE는 다음과 같습니다.

이 문제는 변수분리법(Separating Variables)을 이용해서 비교적 쉽게 해결할 수 있습니다.
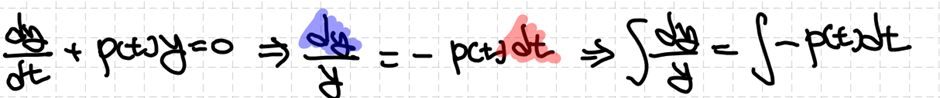
변수분리법은 적분하고자 하는 변수들을 한 곳에 몰아 적분을 비교적 편하게 수행하도록 하는 기법입니다. 이 상황에서는 dy 와 dt를 각 항으로 분리해서 식을 다시 작성할 수 있습니다.
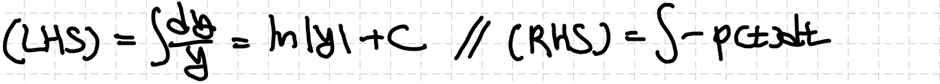
왼쪽 항은 적분이 가능하지만 오른쪽 항은 p(t)의 형태에 의존하기에 문제 상황에 맞게 계산해야 합니다.

적분상수는 결국 초기조건에 의해 결정됩니다. 그렇기에 위의 과정을 거쳐 식을 정리할 수 있습니다.
예시 상황을 들어 초기조건을 적용하는 방법을 보여드리고자 합니다.
EX


이때 * 과정을 이해하기 조금 어려울 수 있습니다. 표현만 같은 거지 엄밀하게 따지만 다른 상수이긴 하지만, 결국 초기조건에 의해서 정해지는 값이므로 표현해둔 것입니다. 초기조건을 대입해서 상황에 적합한 해를 얻을 수 있습니다.

2) 비제차 1차 선형 상미분방정식 (Inhomogeneous 1st order Linear ODE)
초기조건(IC)이 주어진 inhomogeneous ODE는 다음과 같습니다.

inhomogeneous ODE는 ODE의 일반형이라고 생각할 수 있습니다. 이 ODE의 해는 적분인자(Integrating Factor)를 이용해서 유도할 수 있습니다. 그 결과는 다음과 같습니다.

여기서 C는 문제 조건에 의해 정해질 것입니다.
다만 이 공식을 적용할 때 유의해야 하는 부분이 있습니다. 1차 미분된 항 앞의 계수가 1임을 반드시 확인해야 합니다. 예시를 통해서 살펴보겠습니다.

주어진 미분방정식의 1차항 계수가 3이기 때문에 이를 1로 만들어야 하고, 이를 위해 3으로 나누어서 다시 ODE를 작성한 것입니다. 이를 위의 식에 넣어서 계산할 수 있습니다.

초기조건을 이용해서 상수 C를 결정할 수 있습니다.

나타나는 해의 형태를 다시 정리했을 때 homogeneous ODE 였을 때의 해에 특수해가 더해진 것임을 다시 한번 확인할 수 있습니다.
'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 5. 라그랑쥐의 차수축소법 (0) | 2022.03.13 |
|---|---|
| 부록 1 미분방정식과 조건설정 (0) | 2022.03.11 |
| 4. 2차 선형 상미분방정식의 전반적인 개념 (0) | 2022.03.11 |
| 3. 1차 선형 상미분방정식 (2) 라플라스 변환의 적용 (1) | 2022.03.10 |
| 1. 상미분방정식의 형태 및 문제풀이 접근방법 (0) | 2022.03.09 |