
Contents
1. 차수축소법 (the Reduction of Order)
2차 상미분방정식의 해를 표현하기 위해서 2개의 일차독립인 해의 기저가 필요합니다. 하지만 몇몇 경우 풀이의 결과로 단 하나의 해의 기저만 확인되는 경우가 있습니다. 예를 들어 $y_1=y_2$일 때도 일반해를 표현할 수 없게 됩니다. 따라서 $y_1$에 대해 독립이고 미분방정식에 해의 기저로 작동할 수 있는 또 하나의 해를 찾을 필요가 있습니다. 라그랑쥐의 차수축소법(the Reduction of Order)을 이용하면 또다른 해 $y_2$를 얻을 수 있습니다.
1. 차수축소법 (the Reduction of Order)
$y_1$을 제차 2차 선형 ODE를 풀이한 결과 얻은 하나의 해라고 생각해봅시다. 차수축소법을 이용하면 $y_1$과 독립이고 주어진 2차 ODE를 충족하는 또 다른 해 $y_2$를 얻을 수 있습니다.

이 식을 무조건 외우라고만 하면 어려움을 느낄 수 있습니다. 그렇기에 유도과정을 간략하게 살펴보겠습니다.

우선 $y_2$를 위의 형태를 따를 것이라고 생각하고, ODE에 넣어서 식을 정리할 수 있습니다.

이때 정리된 식에서 우리가 풀어야 하는 것은 $u$입니다. $y_1$은 이미 계산된 해이기 때문입니다. 하지만 우리는 아직 1차 ODE만 풀 수 있기에 $u’$을 치환해서 식을 계속 풀어나갈 수 있습니다.

$U$에 대한 1차 미분방정식을 풀이하면 $t$에 대해 정리된 식을 얻을 수 있습니다. 하지만 우리는 $u$를 구해야 하는 것이므로 치환된 형태를 다시 환원해야 합니다.
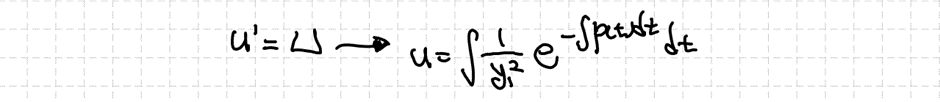
이 결과를 이용하면 우리는 $y_2$를 얻을 수 있을 것입니다. 사실 문제를 풀이할 때 이처럼 유도를 하나하나 하면 시간이 오래 걸립니다. 그렇기에 요약된 알고리즘을 살펴보겠습니다.

검은색 화살표 순서대로 정의를 한 후, 다시 역순으로 풀이를 해주기만 하면 $y_2$를 얻을 수 있습니다.
예시를 통해 이해해보겠습니다.

해당 2차 ODE를 풀면 $y_1$만 얻게 됩니다. 그렇기에 차수축소법을 이용해서 $y_2$를 구한 것입니다. 새로 구한 해가 미분방정식의 해가 될 수 있는지 알고 싶으면 이를 다시 대입하면 됩니다. 그 과정은 다음과 같습니다.

'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 7. 미정계수법을 이용한 상수계수를 갖는 비제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
|---|---|
| 6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
| 부록 1 미분방정식과 조건설정 (0) | 2022.03.11 |
| 4. 2차 선형 상미분방정식의 전반적인 개념 (0) | 2022.03.11 |
| 3. 1차 선형 상미분방정식 (2) 라플라스 변환의 적용 (1) | 2022.03.10 |