
Contents
1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이
2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이
미분방정식 풀이과정을 따르지 않더라도 1차 상미분방정식을 풀이할 수 있습니다. 라플라스 변환을 이용해서 대수식을 정리하고 다시 라플라스 역변환을 이용하면 미분방정식의 해를 구할 수 있습니다.
1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이
예시를 통해서 라플라스 변환을 이용해서 ODE를 풀어내는 방법을 살펴보겠습니다.
EX
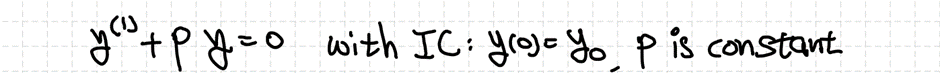
우선 각 항에 라플라스 변환을 취해서 식을 대수 영역으로 전환해줍니다.

그 후 라플라스 변환이 취해진 해에 대해 식을 다시 정리할 수 있습니다.

우리가 원하던 해는 대수방정식의 해가 아니라 미분방정식의 해이기 때문에 위의 결과에 라플라스 역변환을 취해줍니다. 그러면 미분방정식의 해를 얻을 수 있습니다.
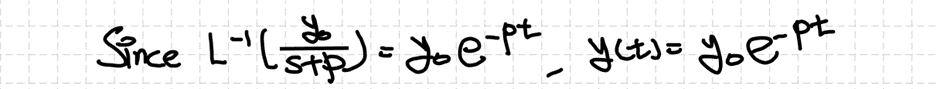
2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이

제차 미분방정식을 풀이할 때와 마찬가지로 라플라스 변환을 취하고, 라플라스 변환된 해에 대해 식을 정리할 수 있습니다.

정리된 식의 형태를 살펴보면 homogeneous 일 때의 해($Y_h(s)$)와 특수해($Y_p(s)$)의 조합인 것을 확인할 수 있습니다. 이제 라플라스 역변환을 취하면 미분방정식의 해를 구할 수 있을 것입니다.
이해를 위해 예시를 살펴보겠습니다.
EX

우선 라플라스 변환을 취해서 대수방정식을 얻은 후 식을 정리합니다.

이제 라플라스 역변환을 취해 식을 정리해주어야 하는데, 이를 위해서 식을 재정리할 필요가 있습니다. 보통 라플라스 역변환을 위한 식 정리는 유리식의 항등성을 이용합니다.

라플라스 역변환을 취하면 미분방정식의 해를 얻을 수 있습니다.
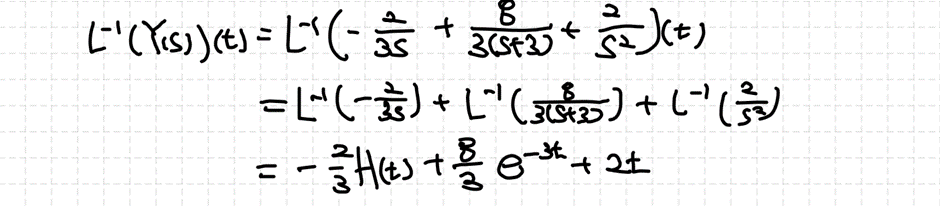
여기서 $H(t)$는 Heviside Step Function이고, 주어진 미분방정식을 $t>0$에 대해 고려하면 $H(t)=1$로 두고 미분방정식의 해를 사용하면 됩니다. (사실 $t$가 시간인 경우가 많아 $t>0$에 대해서 고려하긴 합니다.)
'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 5. 라그랑쥐의 차수축소법 (0) | 2022.03.13 |
|---|---|
| 부록 1 미분방정식과 조건설정 (0) | 2022.03.11 |
| 4. 2차 선형 상미분방정식의 전반적인 개념 (0) | 2022.03.11 |
| 2. 1차 선형 미분방정식의 풀이 (1) (0) | 2022.03.09 |
| 1. 상미분방정식의 형태 및 문제풀이 접근방법 (0) | 2022.03.09 |