
Contents
미정계수법 (Method of Undetermined Coefficients)
미정계수법 (Method of Undetermined Coefficients)
미정계수법은 forcing function $r(t)$과 형태가 유사하게 특수해 $y_p (t)$를 설정해서 해를 구하는 것입니다. $y_p (t)$를 주어진 상미분방정식에 대입한 후 항등식의 결정방법 중에서 계수비교법을 이용해서 해를 결정합니다. forcing function의 형태에 따라 설정하게 되는 $y_p (t)$를 아래에 정리했습니다.

풀이과정은 다음과 같습니다.
Step 1 제차 방정식의 풀이
주어진 미분방정식에서 forcing function을 0으로 설정할 때 생기는 제차 미분방정식을 풀어줍니다. 혹시 그 방법을 모르겠다면 아래의 링크를 참고하면 되겠습니다.
6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 :: 화공&책 리뷰 (tistory.com)
Step 2 특수해의 설정
위의 표를 참고해서 forcing function의 형태에 맞게 $y_p(t)$를 설정하고 대입한 후 계수비교를 통해서 형태를 결정합니다.
예시를 통해 설명해보겠습니다.
EX
주어진 문제가 다음과 같다고 하겠습니다. 우선 forcing function $e^t=0$으로 두면 제차 상미분방정식으로 형태가 변하고, 이는 특성방정식을 이용해서 풀이할 수 있습니다.

forcing function이 지수함수 형태를 띠고 있음을 이용해서 해를 결정할 수 있습니다. 그리고 주어진 초기조건을 이용해서 유일한 해 하나를 찾을 수 있습니다.
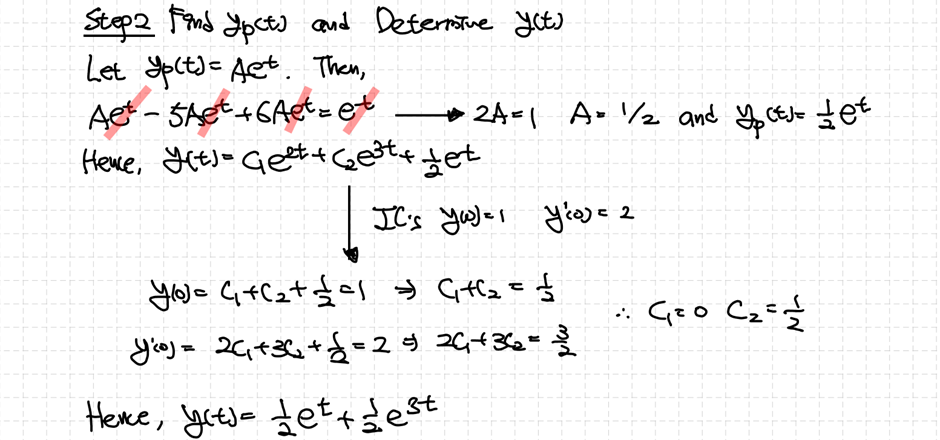
** 주의사항 **
만약 $y_p(t)$에 $y_h(t)$ 형태 중 일부를 포함하고 있다면 새롭게 $y_p(t)$를 설정해야 합니다. 이는 $t^k y_p(t)$로 설정하는 것을 의미합니다. 이때 $k$는 제차 ODE의 해의 형태와 겹치는 것이 없을 때 까지 그 크기를 높여주어야 합니다. 예를 들어보겠습니다.

위의 예시에서 $r(t)$만 $e^{3t}$로 바꾼 문제입니다. 하지만 이 forcing function은 $y_h(t)$에서 이미 등장하는 형태입니다. 그렇기에 아무리 $y_p(t)$를 결정하더라도 결국 $y_h(t)$에 흡수되어 제차 상미분방정식에 대한 해 밖에 얻지 못합니다. 따라서 $y_p(t)=Ate^{3t}$로 두고 식을 풀어야 합니다.

'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 9. 변수계수를 갖는 제차 2차 상미분방정식의 소개와 예시: 오일러-코시 방정식 (0) | 2022.03.15 |
|---|---|
| 8. 매개변수 변환법을 이용한 상수계수를 갖는 비제차 2차 상미분방정식의 풀이 (0) | 2022.03.15 |
| 6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
| 5. 라그랑쥐의 차수축소법 (0) | 2022.03.13 |
| 부록 1 미분방정식과 조건설정 (0) | 2022.03.11 |