
Contents
매개변수 변환법 (the method of Variation of Parameter)
미정계수법은 상수계수를 갖는 2차 ODE를 풀이하기에 좋은 방법이지만, 시간이 비교적 오래 걸리는 단점이 있습니다. 그리고 $y_p(t)$의 형태가 $y_h(t)$에 포함되어 있는지도 해를 구하기 전에 미리 예측해야 하는 번거로움이 있습니다. 이러한 문제점들을 보완하기 위해 매개변수 변환법(method of Variation of Parameter)을 이용할 수 있습니다.
매개변수 변환법 (the method of Variation of Parameter)
1) 매개변수 변환법 개념
다음과 같은 미분방정식이 주어졌다고 생각하겠습니다.
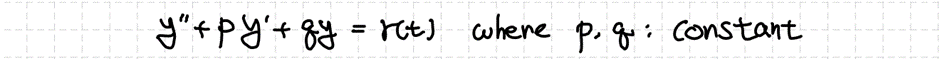
이때 매개변수 변환법을 이용해서 $y_p(t)$를 구하는 것은 해의 형태를 아래처럼 둔다는 것을 뜻합니다

즉, 주어진 미분방정식이 제차 ODE일 때 얻은 해의 기저들의 계수를 하나의 변수로 두고, 이를 풀이해서 $y_p(t)$를 얻는 것입니다. 각각의 매개변수 계수 $u(t)$와 $v(t)$는 다음과 같습니다.

예시를 통해 이해해보도록 하겠습니다.
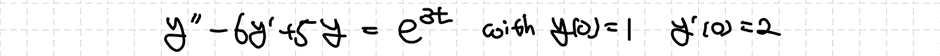
우선 제차 상미분방정식일 때의 해 $y_h(t)$일 때의 해부터 구하겠습니다.

그리고 매개변수 변환법을 이용해서 $y_p(t)$를 구할 수 있습니다.

그리고 주어진 초기조건을 이용해서 조건에 적합하는 유일한 해를 구할 수 있습니다.
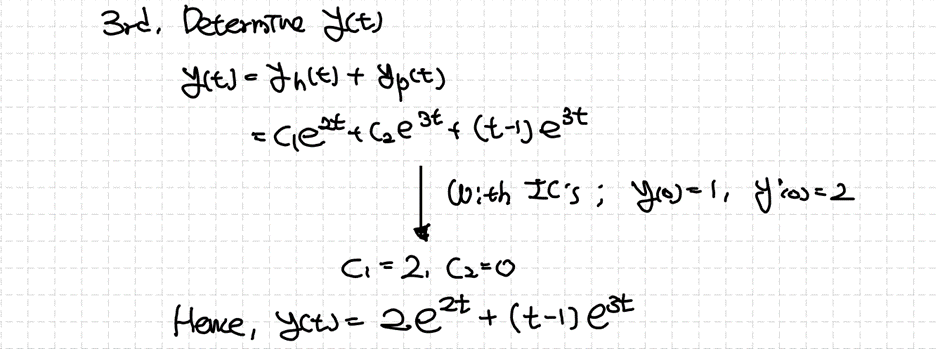
2) 의의와 한계
매개변수 변환법을 이용하면 상수계수를 갖는 모든 2차 상미분방정식을 풀이할 수 있습니다. 또는 오일러 코시 상미분방정식 (Euler-Cauchy ODE, $t^2y’’+ty’+y=r(t)$)를 풀이할 수 있습니다. 하지만, 변수를 계수로 갖는 2차 상미분방정식을 풀이하는 데에는 제한이 있습니다. 이러한 미분방정식을 풀 때는 급수해(Series Solution)를 이용하거나 수치해석(Numerical Analysis)를 이용합니다.
'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 10. 변수계수를 갖는 제차 2차 상미분방정식 풀이를 위한 급수의 이해 (0) | 2022.03.15 |
|---|---|
| 9. 변수계수를 갖는 제차 2차 상미분방정식의 소개와 예시: 오일러-코시 방정식 (0) | 2022.03.15 |
| 7. 미정계수법을 이용한 상수계수를 갖는 비제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
| 6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
| 5. 라그랑쥐의 차수축소법 (0) | 2022.03.13 |