
Contents
오일러-코시 방정식(Euler-Cauchy Equation)
지금까지는 상수만을 계수로 갖는 2차 상미분방정식들에 대해서만 살펴봤습니다. 하지만 많은 상미분방정식들은 계수들을 변수로 갖는 경우가 많습니다. 이때 우리는 급수해(Series Solution)을 이용해서 미분방정식의 해를 표현합니다. 이번에는 변수계수를 갖는 미분방정식의 예시인 오일러-코시 방정식(Euler-Calucy Equation)에 대해 살펴보고자 합니다.
오일러-코시 방정식(Euler-Cauchy Equation)
1) 형태
오일러-코시 방정식의 형태는 아래와 같고, 2차 ODE에 대해서도 정리할 수 있습니다.
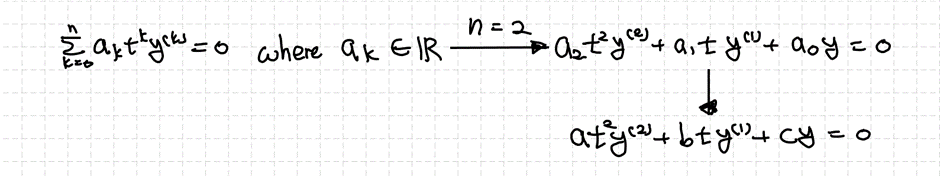
편의를 위해서 계수들을 각각 $a, b, c$로 표현한 것입니다.
2) 풀이
오일러-코시 방정식 풀이는 제차 2차 ODE를 풀이하는 것과 그 방식이 유사합니다. 우선 모든 단계를 전체적으로 살펴보겠습니다.
Step 1 trivial solution을 둔다. ($y(t)=t^m$)
Step 2 설정한 해를 방정식에 다시 대입해서 특성방정식을 얻는다. ($am ^2+(b-1)m+c)$)
Step 3 특성방정식에 따라 해의 형태를 결정한다.
상수계수를 갖는 제차 2차 ODE에서는 $y(t)=e^{λt}$로 설정한 것에서 $y(t)=t^m$으로 바꾸어 설정한 것이 변했고, 그래서 특성방정식도 다른 형태로 얻어진 것입니다. 그러면 특성방정식의 판별식의 부호에 따라 작성되는 식의 형태도 차이가 있음을 예상할 수 있을 것입니다. 조금 더 구체적으로 살펴보겠습니다.
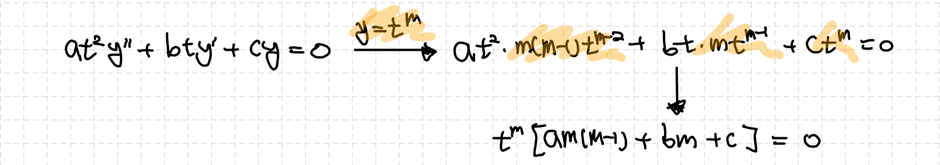
설정한 식을 오일러-코시 방정식에 넣으면 식을 정리할 수 있습니다. 주어진 식이 만족하려면 $t^m=0$이거나 $m$에 대한 방정식이 0이여야 합니다. 하지만 $t^m=0$일 때 오일러-코시 방정식이 성립하는 것은 자명합니다. 그렇기에 해에서 어떠한 의미도 가져올 수 없습니다. 따라서 우리에게 의미가 있는 해를 얻기 위해서 필요한 조건은 $m$에 대한 방정식이 0인 것이고, 이를 특성방정식으로 생각할 수 있습니다. 좀 더 편한 계산을 위해 이 방정식을 $m$에 대해 정리할 수 있고 그 결과는 다음과 같습니다.
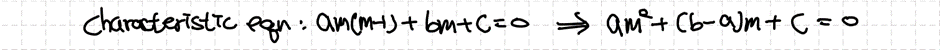
특성방정식이 $m$에 대한 2차방정식이므로 이를 계산해서 풀이할 수 있습니다. 하지만 특성방정식에서의 판별식 $D=(b-a)^2-4ac$의 부호에 따라 $m$의 형태가 달라질 것입니다. 각각의 경우 해가 어떻게 다르게 나타나는지 살펴보겠습니다.
3) $D$의 부호에 따른 해의 형태
(1) $D>0$: Real, two different roots
판별식의 부호가 양수라면 서로 다른 2개의 실근 $m_1, m_2$가 나올 것입니다.

(2) $D<0$: Complex, two different roots
판별식의 부호가 음수라면 복소수 형태를 갖는 서로 다른 2개의 실근이 얻어질 것입니다.

보다 편한 논의를 위해서 근의 실수부분을 $α$, 근의 복소수부분을 $β$라고 정의한 것입니다. 이를 이용해서 해를 표현하겠습니다.

비교적 해의 형태가 간단하게 바뀌었지만, 여전히 지수에 허수 $i$가 있어서 계산 시에 불편할 수 있습니다. 이 문제는 Euler Identity를 이용해서 식의 형태를 편하게 바꿀 때 해결할 수 있습니다. 밑을 자연상수로 갖지 않는 형태이더라도 약간의 식의 변형을 통해 Euler Identity를 사용할 수 있습니다.

이를 이용해서 해를 정리할 수 있습니다.

(3) $D=0$ Double Root
판별식이 0일 때에는 하나의 해만 얻을 수 있기 때문에 차수축소법(Reduction of Order)을 이용해서 또 다른 기저해를 찾을 필요가 있습니다. 차수축소법을 모르거나 기억이 나지 않으면 아래의 링크를 참고하면 될 것 같습니다.
5. 라그랑쥐의 차수축소법
Contents 1. 차수축소법 (the Reduction of Order) 2차 상미분방정식의 해를 표현하기 위해서 2개의 일차독립인 해의 기저가 필요합니다. 하지만 몇몇 경우 풀이의 결과로 단 하나의 해의 기저만 확인되는
cccforone.tistory.com

이때 $p(t)$가 어떠한 미분방정식에서 오는지 확인할 필요가 있습니다.

라그랑쥐 차수축소법 이용 시 적용하는 $p(t)$는 미분방정식의 최고차항 계수가 1일 때를 이야기한 것이므로 $b/(at)$인 것을 확인할 수 있습니다. 마저 $y_2$를 찾고 해를 결정하겠습니다.

아마 첫번째 줄에서 절댓값을 날리는 과정이 이해가 안될 수 있는데, 이는 끌고가서 계산을 하더라도 결국 $c_2$에 포함될 것을 감안하여 미리 계산의 편의를 위해 부호를 무시한 것입니다.
'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 11. 비특이점에서의 변수계수를 갖는 2차 상미분방정식의 해와 르장드르 방정식 (0) | 2022.03.16 |
|---|---|
| 10. 변수계수를 갖는 제차 2차 상미분방정식 풀이를 위한 급수의 이해 (0) | 2022.03.15 |
| 8. 매개변수 변환법을 이용한 상수계수를 갖는 비제차 2차 상미분방정식의 풀이 (0) | 2022.03.15 |
| 7. 미정계수법을 이용한 상수계수를 갖는 비제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |
| 6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 (0) | 2022.03.14 |