
Contents
르장드르 방정식(Legendre Equation)과 미분방정식의 풀이
멱급수를 이용해서 미분방정식의 해를 구하는 과정을 살펴보고자 합니다. 특이점을 갖지 않는 르장드르 방정식(Legendre Equation)을 이용해서 이해를 돕고자 합니다.
르장드르 방정식(Legendre Equation)과 미분방정식의 풀이
1) 르장드르 방정식(Legendre Equation)의 형태
르장드르 방정식의 형태는 다음과 같습니다.

만약 t=1또는 t=−1에서 해석을 하면 Singular point이기 때문에 계산 과정이 복잡하겠지만, 르장드르 방정식의 사용 범위는 특이점을 포함하지 않습니다. 이 사실을 이용해서 르장드르 방정식의 해를 찾도록 하겠습니다.
2) 멱급수를 이용한 상미분방정식의 풀이
특이점을 갖지 않는 상미분방정식의 해를 구하는 과정을 요약하면 다음과 같습니다.
Step 1 Trial Solution을 설정하고 이를 주어진 미분방정식에 대입해서 식을 정리한다.
Step 2 Index number n을 조정하여 미분방정식이 성립되기 위해 필요한 조건들을 찾는다.
Step 3 일반해를 찾는다.
이제 직접 식을 풀어보며 단계별로 구체적인 설명을 드리겠습니다.
Step 1 Trial Solution을 설정하고 이를 주어진 미분방정식에 대입해서 식을 정리한다.
t=0에서의 해를 구해보겠습니다. Trial Solution과 해의 미분형태를 얻을 수 있습니다.

급수에 대해 미분을 한 것이므로 index number n이 미분횟수만큼 증가한 것을 확인할 수 있습니다. 이들을 주어진 르장드르 방정식에 대입해서 식을 정리할 수 있습니다.

Step 2 Index number n을 조정하여 미분방정식이 성립되기 위해 필요한 조건들을 찾는다.
자명한 해 t=0이 아닌 다른 해를 얻는 것이 미분방정식 풀이의 목적입니다. 급수 기호에 포함된 일반항들(이하 피급수항)이 모두 0으로 표현된다면 급수도 0으로 나타나질 것입니다. t의 지수부분을 통일하면, 급수를 정리할 수 있습니다. 이를 위해서 급수의 index number n을 조정하는 것입니다. 보통 가장 높은 차수를 갖고 있는 t에 대한 지수로 통일을 합니다. 좀 더 살펴보겠습니다.

주어진 각 항들을 전개했을 때 n=2부터는 급수를 이용해서 간단하게 표현할 수 있음을 확인할 수 있습니다. 이를 위해서 index number을 조정해야 합니다. 여기서 가장 높은 t의 차수가 n이기 때문에 이에 맞추어 가장 첫번째 급수의 index number을 바꿔줘야 합니다.

수열의 합을 이용한 표현은 결국 무수한 합을 편리하게 표현하기 위해 사용된 것입니다. 그렇기에 올바르게 index number을 조정했다면 급수는 같아야 합니다. 위에서의 index number 조정은 n−2를 n으로 바꾼 것이기 때문에 나머지 n들도 모두 2씩 증가하도록 표현한 것입니다. (n−2=k라고 치환했다고 생각하면 이해하기가 더 편할 것입니다.) 조정된 급수를 이용해서 식을 정리하면 아래와 같습니다.

정리한 식이 임의의 t에 대해 성립하기 위해서는 t에 대한 계수가 0이면 됩니다. 이를 이용해서 미분방정식이 0이기 위한 조건들을 얻을 수 있습니다.

이때 λ=m(m+1)이라고 하고 식을 한 번 더 정리할 수 있습니다.
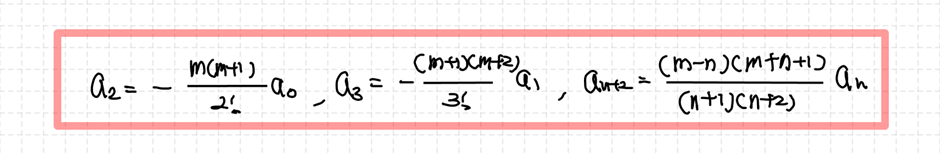
Step 3 일반해를 찾는다.
위에서 얻은 조건을 바탕으로 일반해를 표현할 수 있습니다. 우선 위에서 a_2는 a_0로부터 시작하고 a_3이 a_1으로부터 시작하기 때문에 우리는 홀수-홀수 짝수-짝수 관계인지를 생각해볼 수 있습니다. 그리고 주어진 조건에서 점화식이 n - n+2관계를 보입니다. 이는 n과 n+2가 모두 홀짝이 동일한 것을 의미합니다. 즉, a_{2n-1}은 a_1로부터 확장되고, a_{2n}은 a_0으로부터 확장되는 사실을 알 수 있습니다. 이를 생각하여 일반해를 표현할 수 있습니다.
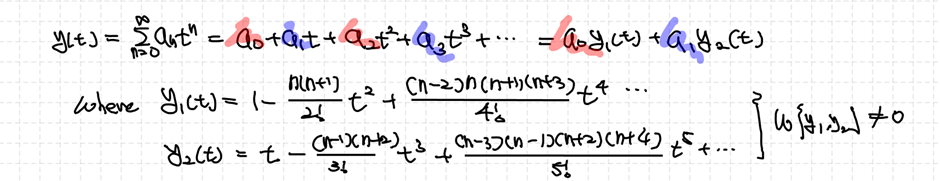
'전공 개념.zip > 상미분방정식 (ODE's)' 카테고리의 다른 글
| 13. 라플라스 변환을 이용한 2차 선형 상미분방정식의 풀이 (0) | 2022.03.16 |
|---|---|
| 12. 특이점에서의 변수계수를 갖는 2차 상미분방정식의 해와 프로베니우스 방법 (0) | 2022.03.16 |
| 10. 변수계수를 갖는 제차 2차 상미분방정식 풀이를 위한 급수의 이해 (0) | 2022.03.15 |
| 9. 변수계수를 갖는 제차 2차 상미분방정식의 소개와 예시: 오일러-코시 방정식 (0) | 2022.03.15 |
| 8. 매개변수 변환법을 이용한 상수계수를 갖는 비제차 2차 상미분방정식의 풀이 (0) | 2022.03.15 |