Contents
1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)
푸리에 변환의 형태와 대칭성이 고려되었을 때의 푸리에 변환을 같이 살펴보겠습니다.
2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)
푸리에 변환이 갖는 몇가지 대수적 특성들에 대해 살펴볼 것입니다.
3. 파르스발 이론 (Parseval's Theorem)
함수와 푸리에 계수 사이의 관계를 설명하는 파르스발 이론에 대해 살펴보고, 이 이론이 가져다주는 의의에 대해 간략하게 살펴볼 것입니다.
1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)
1) 푸리에 변환의 의의
푸리에 변환은 주기성을 갖는 함수들에만 적용 가능했던 푸리에 급수의 단점을 극복한 적분 변환 기법입니다. 그 결과 이 변환법은 다양한 분야에서 사용되게 됩니다. 그 중에서도 통신에 대해 공부하는 사람들은 푸리에 변환을 수없이 살펴보게 될 것입니다. 푸리에 변환을 통해 시간 영역에서 정의된 함수를 주파수 영역으로 전사(mapping)하여 여러 해석을 용이하게 돕습니다.
2) 푸리에 변환의 수학적 형태
(1) 푸리에 변환의 관계와 형태
푸리에 변환 $F$에 대해 원함수와 변환된 함수는 아래의 관계를 갖습니다.

어떠한 함수에 푸리에 변환($F$)을 취하면 주파수 함수를 얻을 수 있으며, 반대로 푸리에 역변환($F^{-1}$)을 취하면 원래의 함수를 얻을 수 있습니다.
푸리에 변환과 역변환의 수학적 형태는 다음과 같습니다.
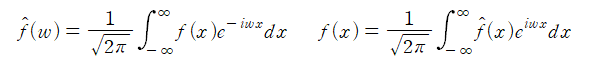

어떠한 함수에 $F$또는 $F^{-1}$를 취했을 때 사용자가 원하는 함수를 얻는 것을 알 수 있습니다.
(2) 대칭성을 갖는 함수에 대한 푸리에 변환
만약 푸리에 변환을 취하려는 함수가 기함수 또는 우함수라면 푸리에 변환을 특수하게 표현하며, 이를 푸리에 사인/코사인 변환(Fourier Sine/Cosine Transformation)이라고 합니다. 만약 원래 함수가 기함수라면 푸리에 사인 변환을, 우함수라면 푸리에 코사인 변환을 취할 수 있습니다. (푸리에 급수와 유사한 것을 알 수 있습니다.) 각 변환의 수학적 형태를 살펴보겠습니다.
푸리에 사인 변환 (Fourier Sine Transformation)

푸리에 코사인 변환 (Fourier Cosine Transformation)

원래의 푸리에 변환과 약간 형태가 상이하여 의문을 가질 수도 있다 생각됩니다만, 결국 똑같습니다. 왜냐하면 대칭성에 의해 적분 구간을 반으로 줄이더라도 적분값을 2배로 하면 그 결과가 같기 때문입니다. (일전에 대칭성을 갖는 함수의 푸리에 급수를 다뤄보며 언급했으므로 참고하시면 될 것 같습니다.)
2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)
푸리에 변환의 몇가지 특성을 알아보기 위해 한 가지 약속을 하겠습니다. $f(x)$와 $g(x)$는 각각 푸리에 변환을 취할 수 있는 함수이며, 그 관계는 아래와 같습니다.

이 약속을 전제하고 푸리에 변환의 수학적 특성을 설명하겠습니다.
1) 선형성 (Linerarity)
푸리에 변환은 라플라스 변환과 마찬가지로 선형 연산자입니다. 선형성은 가산성(additivity)와 동차성(homogeneity)이 동시에 성립할 때 보장됩니다. 이는 적분 자체가 선형적인 연산자이기 때문인데, 이를 수학적으로 표현하면 다음과 같습니다.

선형성은 푸리에 변환에 $f(x)$대신 $af(x)+bg(x)$를 대입한 후, $f$와 $g$에 대한 푸리에 변환으로 분리하면 쉽게 얻어낼 수 있습니다.
2) 도함수에 대한 푸리에 변환 (Fourier Transformation of Derivatives)
n번 미분할 수 있는 어떠한 함수 $f$에 푸리에 변환을 취할 수 있습니다.

이 성질은 수학적 귀납법을 이용해서 증명을 할 수 있습니다. 자세한 증명 과정은 생략하고, 기회가 될 때 다루어보겠습니다.
3) 푸리에 변환의 합성곱 (Convolution of Fourier Transformation)
라플라스 변환에서와 마찬가지로 푸리에 변환에 대한 합성곱(Convolution)을 정의합니다. 형태는 다음과 같ㅅ브니다.

이를 이용했을 때 푸리에 변환된 서로다른 두 함수가 곱해져있을 때, 푸리에 역변환을 취해서 원래의 함수를 얻을 수 있습니다.

증명 방법은 라플라스 변환의 합성곱과 동일하며, 증명 과정은 따로 자세히 설명하지 않겠습니다.
3. 파르스발 이론 (Parseval's Theorem)
1) 파르스발 이론과 푸리에 급수 (Parseval's Theorem and Fourier Series)
푸리에 급수에 대해 파르스발 이론은 푸리에 급수는 계수들의 정보로 표현될 수 있음을 뜻합니다. 정확히 얘기하자면 주기 함수의 내적(inner product)은 푸리에 계수 사이의 내적과 일정한 관계를 보입니다.
$f(x)$와 $g(x)$가 동일한 주기를 $T$로 갖는 주기함수라고 하고, 복소지수함수를 포함한 푸리에 급수에서의 푸리에 계수를 각각 $c_k$, $d_k$라고 하겠습니다. 이때, 두 함수 사이의 내적은 푸리에 계수 사이의 내적과 일정한 관계를 갖습니다.

이때 $f(x)=g(x)$인 상황을 생각해보면, 다른 의미를 얻을 수 있습니다. 이 경우 같은 함수의 내적을 통해 얻은 함수의 크기가 결국 계수의 크기와 동일하다는 것을 알 수 있게 됩니다. 식으로는 다음과 같이 표현할 수 있습니다.

2) 파르스발 이론과 푸리에 변환 (parseval's Theorem and Fourier Transformation)
푸리에 변환에서의 파르스발 이론도 결국 동일한 이야기를 합니다. 간단히 설명하고 넘어가겠습니다.

여기까지가 편미분방정식을 본격적으로 시작하기 전에 간략하게나마 다루어본 푸리에 급수와 푸리에 변환 내용입니다. 푸리에 변환에 대한 전반적인 내용이 필요 없더라도 푸리에 급수에서 푸리에 계수 정보를 얻어내기 위해 내적과 직교성을 이용한 방법은 꼭 숙지하셨으면 좋겠습니다. 편미분방정식의 해를 특정하는 데에도 동일한 방법이 사용되기 때문입니다. 복습을 위해
다음부터는 스트룸-리우빌 정리(Strum-Liouville Theory)와 초기/경계조건(Initial/Boundary Condition)에 대해서 살펴보겠습니다.