Contents
1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)
- 미분방정식을 풀이하는 데 있어 필요한 조건들에 대해 간략히 소개합니다. 초기 시점에 비중을 둔 초기조건과 공간에 비중을 둔 경계조건에 대해 설명을 드리고자 합니다. 주어진 미분방정식의 해를 특정하기 위해 필요한 조건의 개수에 대해 논의해보고, 물리학에서 경계조건의 중요성에 대해서도 말씀드리겠습니다.
2. 경계조건의 분류 (the Classification of Boundary Condition)
- 경계조건을 구분하는 것은 생각보다 중요한 일인데, 이러한 이유와 경계조건의 종류를 살펴보겠습니다.
0. Introduction - 조건설정의 필요성 (the Necessity of Setting Conditions)
본격적인 내용에 들어가기 앞서 한가지 내용을 먼저 같이 생각해보려 합니다. 우리는 왜 미분방정식을 풀이하는 것에 대해 배워야 할 필요가 있을까요? 여러 이유를 들 수 있습니다. 제 생각에는 지배방정식(Governing Equation)을 풀이하기 위해 미분방정식을 공부해야 한다고 생각합니다.
지배방정식은 어떠한 상황에서 알고 있는(또는 측정할 수 있는) 변수들과 우리가 알고 싶은(또는 측정해야 하는) 변수들 사이의 관계를 나타내는 식입니다. 이들은 특정 시점($t$)과 미소 시간이 흐른 시점($t+dt$) 사이의 물성 변화로부터 얻어지기 때문에 미분방정식의 형태를 띠는 경우가 많습니다. 수지 방정식(Balance Equation), fin에 대한 열전도 방정식(Heat Conduction) , 1D Box에 놓여있는 입자의 파동방정식(Wave Equation) 등을 예로 들 수 있습니다. 이러한 방정식들을 풀이해야 우리가 원하던 정량적인 정보를 얻을 수 있습니다. 그렇기에 학부수준의 문제를 해결하기 위해서는 미분방정식을 다룰 수 있어야 한다고 생각합니다.
지배방정식들은 놓여있는 조건(상황)에 따라 그 해가 매우 상이합니다. 추후에 같이 살펴보겠지만, 같은 대류현상에 대한 지배방정식을 풀이하더라도 주변이 단열되어있는지, 아니면 일정하게 가열되고 있는지에 따라 편미분방정식의 형태는 매우 다르게 나타납니다. 따라서 우리는 지배방정식에 대한 조건을 올바르게 설정할 수 있어야 합니다.
조건은 크게 2가지로 분류됩니다. 관측시점을 중요시 하는 초기조건(Initial Condition)과 관측위치를 중요시 하는 경계조건(Boundary Condition)이 있습니다. 이제 조건에 대해 본격적으로 얘기해보겠습니다.
1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)
1) 초기조건 (Initial Condition)
초기조건은 어떠한 미분방정식에서 특정 시점에 대한 해의 정보들의 집합을 의미합니다. 초기조건은 시간에 대한 물성 변화를 설명할 때 사용되며, 물체 관측의 시작점($t=0$)에서의 정보를 표현하는 경우가 많습니다. 수식으로 표현하면 다음과 같습니다.

초기조건은 주로 상미분방정식, 또는 편미분방정식 중 시간과 관련된 정보를 결정하는 데 사용됩니다. $n$차 상미분방정식을 결정하기 우해서는 $n$개의 초기조건이 필요합니다.
2) 경계조건 (Boundary Condition)
경계조건은 특정 위치에 대한 해의 정보들의 집합을 의미합니다. 경계조건은 장소(위치)변화에 대한 물성을 표현할 때 사용합니다. 주로 검사체적(Control Volume, system)과 주변(Surrounding)을 구분짓는 경계표면(Control Surface)에 대한 정보들이 주로 나타납니다. 만약 물체가 1D에 놓여있다면 수직선 양 끝 정보가, 3D에 놓여있다면 체적의 표면들에 대한 정보가 표현되어 있을 것입니다. 1D Differential Equation에 대한 경계조건을 수식으로 표현하면 다음과 같습니다.

한번 언급했듯, 편미분방정식의 해는 시공간에서의 물성의 분포를 표현합니다. 그렇기에 편미분방정식에서의 경계조건에 대한 중요성은 매우 높습니다.
3) 해 결정을 위해 필요한 조건의 개수
적절한 종류의 조건을 사용하는 것도 중요하지만, 적합한 해를 찾기 위한 조건의 개수를 아는 것도 중요합니다. 조건의 개수를 너무 많이 부여하면 과적합한 해가 얻어지고, 부족한 개수의 조건을 설정할 경우 해가 정해지지 않습니다.
적합한 해의 개수를 결정하기 위해서는 미분된 변수의 종류와 최고 미분된 횟수를 고려하면 됩니다. 시간에 대한 미분의 차수와 공간에 대한 미분의 차수를 파악한 후 시간에 대한 미분에는 초기조건을 부여하고, 공간에 대한 미분에는 경계조건을 설정하면 됩니다. 예를 들어 보겠습니다.
어떤 편미분 방정식이 시간에 대해 1차 미분, 공간에 대해 2차 미분이 되어있다면 1개의 초기 조건과 2개의 경계조건이 필요합니다.
미분은 정보를 소거하는 연산이고, 적분은 정보를 확장하는 연산입니다. 미분방정식을 푼다는 것은 결국 적분을 거쳐 해를 얻는 것을 의미하기에, 미분된 횟수만큼 적분을 해주어야 합니다. 이는 미분된 횟수만큼의 조건을 필요로 한다는 것으로 해석할 수 있습니다.
예를 들어 보겠습니다.
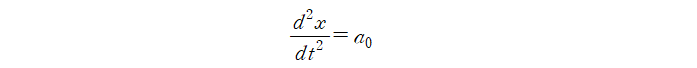
이 미분방정식은 등가속도 운동을 표현하는 간단한 형태의 미분방정식입니다. 이를 풀이하는 과정은 아래와 같습니다.

미분방정식은 풀이했지만 아직 조건이 충분히 제시되지 않았습니다. 2계 상미분방정식의 풀이를 위해서 2번 적분한 것을 확인할 수 있을겁니다. $A_0$과 $B_0$이 결정되어야 우리가 원하던 특정한 해를 얻을 수 있는 것입니다. 2개의 적분상수가 결정되어야 하므로 2개의 조건이 필요합니다. 이 문제는 측정할 수 있는 시점에서의 수치를 기반으로 정보를 확장하는 것이므로 초기조건을 설정하여 해를 특정하겠습니다.

이 결과 해는 다음과 같이 표현됩니다.

이 물리적 현상을 관통하는 지배방정식에 조건을 설정하여 풀이했더니 하나의 특정한 해를 얻은 것을 확인할 수 있었습니다.
이 문제에 다른 조건을 설정해서 풀어보겠습니다. 이번에는 경계조건을 걸어보겠습니다. 편하게 논의하기 위해 공간과 관련된 항에 경계조건을 설정하라고 이야기했지만, 좀더 구체적인 경계조건의 표현은 아래와 같습니다.
"경계조건은 정의역의 양 끝 지점에서의 해와 관련된 정보를 제시한 것"
즉 경계조건은 외부의 영향을 직접적으로 받는 지점에서의 정보가 제시된 것임을 알 수 있습니다. 한번 살펴볼까요?

정의역이 $t\in[0,1]$일 때 경계조건이 다음과 같다고 생각해보겠습니다. 이를 해에 대입했을 때 적분상수를 계산할 수 있습니다.
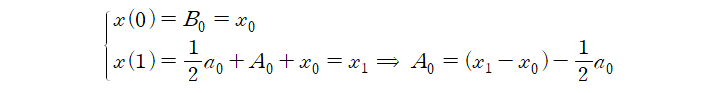
이제 특정한 해를 표현하고 이용할 수 있습니다.

요약하자면 미분방정식의 해를 특정하기 위해서는 조건이 필요하고, 그 개수는 독립변수에 대한 최대 미분 횟수와 동일합니다.
4) 물리학에서 경계조건의 중요성
경계조건은 물리학/공학에서 큰 중요도를 가집니다. 경계에 대한 정보를 갖고 지배방정식을 풀이할 수 있다면 정의된 영역에 대한 모든 정보를 예측할 수 있기 때문입니다. 예를 들어 2D Plate에 대한 문제를 해결해야 한다고 생각해봅시다. 그렇다면 각 변에서의 물성에 대한 정보만 알고 있으면, 2D Plate 전 영역에 대한 물성의 정보를 예측할 수 있다는 것을 의미합니다. 즉, 부분의 정보로부터 전체의 정보를 이끌어내는 것을 가능하게 해주는 것이 경계조건 입니다.
경계는 실험자에게도 유리한 지점입니다. 바로 측정이 가능한 위치이기 때문입니다. 당장 정육면체 내부의 온도 분포를 조사한다고 했을 때, 정육면체 중심보다는 각 면에다가 온도 조절 장치를 설치하는 것이 유리할 것입니다.
실험 설계 측면에서도, 해의 결정에 있어서도 경계조건은 중요한 것은 당연합니다.
2. 경계조건의 분류 (the Classification of Boundary Condition)
편미분방정식을 풀이할 때 유의해야 하는 점이 있습니다. 편미분방정식의 종류에 따라 특정한 해를 얻을 수 있는 경계조건의 형태가 정해져있습니다. 그렇기에 경계조건을 꼭 분류할 수 있어야 합니다. 특히 스투름-리우빌 문제를 풀이하는 데 필요한 경계조건을 일반화해서 표현할 수 있는데, 이는 다음과 같습니다.
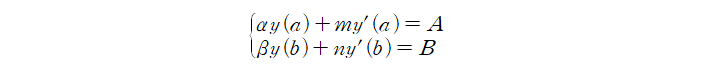
이를 물리적으로 해석해볼 수 도 있겠습니다. $y(a)$는 경계에서의 물리량이 일정하다는 것을 의미합니다. 예를 들어 일정한 온더를 유지하는 열원(Heat Reservior)이 있을 수 있습니다. 반면에 $y'(a)$는 경계에서 물리량의 변화가 일정하다는 것을 의미합니다. 예를 들면 유체의 흐름(flux)가 경계표면에서 일정한 상황을 생각해볼 수 있습니다. 결국 경계조건은 물성에 대한 특정 값 또는 변화량을 포함하고 있을 수 있음을 시사합니다. 계수 $\alpha, \beta, m, n$의 유무에 따라 경계 조건의 종류가 달라집니다.
(1) Dirichlet BC
이 경계조건은 경계지점에서의 물리량들의 값이 제시된 조건을 의미합니다. 즉, 변화를 나타내는 값들의 계수인 $m, n$이 0이 되는 상황을 얘기하는 것입니다.
(2) Neumann BC
이 경계조건은 경계지점에서의 도함수(또는 변화) 정도가 제시된 조건입니다. 즉, 일정한 값을 나타내는 항들의 계수인 $\alpha, \beta$가 0이 되는 상황을 뜻합니다.
(3) mixed Dirichlet-Neumann BC (or Cauchy BC)
이 경계조건은 특정 물리량과 물리량의 변화 정도가 모두 제시된 경계조건입니다.
(4) periodic BC
이 경계조건은 경계지점에서의 물리량이 동일하고, 해당 수치들이 주기적으로 나타나는 조건입니다. 예를 들면 다음과 같습니다.

한편, 위에서 조건들이 갖는 값 $A, B$가 모두 0이라면 이 조건은 제차(homogeneous)라고 하고, 그렇지 않다면 비제차(Inhomogeneous)라고 합니다. 제차 경계조건이 제시된 경우 해를 표현하기 편리하기 때문에 제체화를 할 수 있어야 합니다. 이는 추후 비제차 경계조건이 할당된 편미분방정식을 풀이할 때 같이 살펴보겠습니다.
스투름-리우빌 정리를 공부하다가 갑자기 경계조건에 대해 장황하게 이야기를 한 이유에 대해 궁금할 수 있다고 생각합니다. 이는 바로 다음 글에서 살펴볼 스투름-리우빌 미분방정식의 해의 직교성(Orthogonality)를 보일 때, 경계조건에 대한 논의가 필수적이기 때문입니다. 해당 내용을 다룰 때 다시 한번 설명하겠습니다.
'전공 개념.zip > 편미분방정식 (PDE's)' 카테고리의 다른 글
| 10. 스트룸 리우빌 연산자의 실수 고윳값 증명 (Proof of Real Eigenvalue for Strum Liouville Operator) (0) | 2022.10.11 |
|---|---|
| 9. 스트룸 리우빌 연산자의 자기수반성 증명 (Proof of Self Adjoint of Strum Liouville Operator) (0) | 2022.10.11 |
| 7. 스투름-리우빌 미분방정식의 개념과 형태 (The Concept and Formula of Sturm-Liouville Differential Equation) (0) | 2022.05.15 |
| 6. 푸리에 변환 (Fourier Transformation) (1) | 2022.05.12 |
| 5. 푸리에 적분 (Fourier Integral) (1) | 2022.05.04 |