
Ⅰ. Title
몰질량 측정
Ⅱ. Purpose
1. 이상기체 상태방정식을 이용하여 쉽게 증발하는 기체의 몰질량을 측정한다.
2. 대부분의 기체는 상온, 대기압에서 이상기체 상태방정식을 만족하기 때문에 기체의 부피, 온도, 압력과 함께 용기를 가득 채우는 데에 필요한 물질의 질량 w를 측정하면 이상기체 상태방정식으로부터 몰질량 M을 계산한다.
Ⅲ. Theory
1. 압력(대기압)
1) 개념
어떤 공간에 들어있는 기체 분자는 지속적으로 공간의 벽면에 부딪힌다. 이렇듯 벽면을 밀어내는 힘을 압력(P)라고 하며, 이 힘은 기체 분자와 맞닿아 있는 모든 면에 작용한다. 이를 수식으로 표현하면 다음과 같이 정의할 수 있다.
\[P=\frac{F}{A}\] (A : 압력의 영향을 받는 면적 F: 가해진 힘)
압력은 특정 용기 내에서만 존재하는 개념이 아니라, 지구 전체로 공간을 확대해도 적용되는 개념이다. 지구를 감싸는 대기도 중력의 영향을 받지만 운동 에너지가 중력의 영향보다 크기 때문에 찌그러진 형태는 아니다. 하지만, 중력의 영향 때문에 대기도 지면에 대해 압력을 지니는데 이를 대기압이라고 한다. 대기압은 $1m^2$에 대해 작용하는 공기의 힘의 크기를 측정한다. $1m^2$의 공기의 질량은 약 10,000kg이므로 중력가속도 $g=9.8m/s^2$임을 고려하면 다음과 같은 식을 얻을 수 있다. 이때, 압력의 SI 표준단위가 Pa를 이용해서 표현해보자.
\[P=\frac{F}{A}=\frac{10,000kg\times9.8m/s^2}{1m^2}=1\times10^5N/m^2=10^5Pa\]
하지만, 대기압은 항상 일정하지 않다. 우선, 날씨가 대기압의 크기를 결정짓는다. 대표적으로 습도가 변한다면 대기의 질량이 변화하므로 대기압도 변화할 수 있다. 또한, 위치에 따라 대기압이 변한다. 중력가속도가 위치에 따라 변화하는데, 대기압을 결정짓는 공기의 무게 또한 중력가속도의 영향을 받기 때문이다. 보통 고도가 높은 지역일수록 중력가속도가 작으므로 대기압이 낮다.
2) 측정
공기의 무게도 없다고 생각했던 시절, 토리첼리는 대기압을 측정할 수 있는 기구를 설계했다. 수은을 이용한 이 기구는 수은이 누르는 압력과 대기압이 평형을 이룰 때, 수은기둥이 움직이지 않는 현상을 이용했다. 단위를 이용해서 표현하면 다음과 같다.
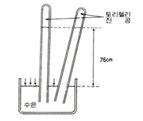
\[1 atm = 760mmHg = 760 torr = 1.01352\times10^5Pa\]
2. 부피
부피를 듣고 물체가 가지는 크기를 떠올릴 수 있을 것이다. 하지만, 기체의 경우 부피는 특별하게 정의된다. 기체의 부피는 들어있는 공간의 크기에 의해 정의된다. 어떤 공간에 여러 종류의 기체가 들어가더라도 기체의 종류에 상관없이 각 가체의 부피는 용기의 크기에 해당한다.
3. 온도
물체가 얼마나 차고 더운지를 수치화한 것이 온도이다. 온도는 기준이 되는 온도를 정하고 이를 어떻게 눈금으로 나누어 표현하는 가를 통해서 3가지로 표현한다.
1) 섭씨온도(Celsius Temperature)
섭씨온도는 대기압이 1기압인 환경에서 물에 대한 정보를 이용해서 표현한 온도다. 물의 어는점과 끓는점을 각각 0℃와 100℃로 하고 두 온도의 사이를 100등분한다. 이때 간격 하나를 1℃라고 한다. 섭씨온도를 측정하기 위해서는 대개 알코올 온도계와 수은 온도계를 사용한다.
2) 화씨온도(Fahrenheit Temperature)
화씨온도도 물에 대한 정보를 이용해서 온도를 표현했다. 물의 어는점과 끓는점을 각각 32℉, 212℉라고 하고, 이를 180등분했다. 이때 나눈 간격을 1℉라고 한다. 화씨온도는 특정지역에서 많이 사용되는 경향이 있지만, 섭씨온도로 바꾸어 표현할 수 있다.
\[T_{F}=\frac{9}{5} \times T_{C}+32\] \[T_{F}\] : 화씨온도, \[T_{C}\] : 섭씨온도
3) 절대온도(Kelvin Temperature)
섭씨온도와 화씨온도는 실생활에서 널리 사용되는 온도체계다. 하지만, 온도를 표현하는 기준을 물로 설정했기에 환경에 의해서 정확하게 측정하지 못하는 경우가 있을 수 있다. 또한 같은 열을 받았더라도 액체의 부피 증가정도가 차이가 있기에 오차가 발생할 수 있다. 이를 방지하기 위해서 물질의 종류와 관계없이 성립하는 이론적인 온도 체계를 만들었다. 이를 열역학적 온도 혹은 절대온도라고 표현한다. 이는 현재 온도에 대해 SI 국제 단위로써 사용되고 있으며, 단위는 K를 이용한다. 절대온도도 섭씨온도를 이용해서 표현할 수 있다. 절대온도와 섭씨온도의 간격은 동일하므로 두 온도 사이의 관계를 다음과 같이 표현할 수 있다.
\[T_{Abs}=273+T_{C}\]
4. 기체분자 운동론 (The Kinetic-Molecular Theory of Gases)
기체분자 운동론을 통해 이상기체가 물리적으로 어떻게 움직이는가를 설명할 수 있다.
1) 기체는 끊임없이 무질서하게 움직인다. (Random motion)
2) 기체의 부피에 대해 기체 분자의 부피는 무시해도 될 정도로 작다. (Negligible molecular volume)
3) 기체 분자 사이의 상호작용(인력, 반발력)은 무시해도 될 정도로 작다. (Negligible forces)
4) 기체분자가 계속 충돌함에도 불구하고, 온도가 일정하다면 기체의 평균운동에너지는 일정하다. 기체의 평균운동에너지는 절대온도에 비례한다. (Constant average kinetic energy & Average kinetic energy proportional to temperature)
5. 보일의 법칙
보일의 법칙은 압력과 부피의 관계에 대해 정의한 법칙이다. 일정한 온도에서 같은 양의 기체가 담긴 용기에 압력을 가해 부피를 감소시키자. 이때, 기체 분자의 평균운동에너지는 일정하지만 벽면에 기체 분자가 충돌하는 횟수가 증가한다. 기체 분자가 벽면에 충돌하는 횟수는 압력의 크기를 의미하므로 압력이 증가함을 알 수 있다. 정리하면, 같은 온도에 대해 같은 몰수인 기체의 부피는 압력에 반비례한다.
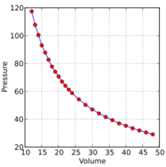
\[V\propto\frac{1}{P}\]
이 그래프는 2가지 특성을 지닌다. 우선, 기체의 몰수가 일정하므로 그래프 위의 각 점에 대해서 부피와 압력의 곱은 항상 기체의 몰수로 일정하다. 또한, 온도가 증가한다면 같은 부피에 대해서 벽면에 기체 분자가 충돌하는 횟수가 증가한다. 이는 압력이 증가함을 의미한다. 따라서 온도가 증가하면 기체의 그래프가 우상향으로 이동한다.
6. 샤를의 법칙
샤를의 법칙은 온도와 부피의 관계를 표현한다. 압력이 일정한 상황에서 같은 몰수의 기체 온도를 높이면 기체의 평균운동에너지가 증가한다. 즉, 기체 분자의 운동 속도가 증가하여 기체 분자가 실린더의 벽면에 충돌하는 횟수 및 세기가 증가한다. 이는 실린더 내부 압력이 증가함을 의미한다. 하지만 외부의 압력과 같아질 때까지 내부의 압력은 감소하며 이 과정에서 실린더의 부피는 증가한다. 정리하자면, 같은 압력과 같은 몰수의 기체에 대하여 온도가 증가하면 기체의 부피도 증가한다.
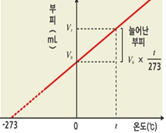
\[V\propto T\]
\[V_{t}=V_{0}+V_{0}\times\frac{t}{273}=V_{0}(1+\frac{t}{273})\]
7. 아보가드로 법칙
아보가드로 법칙은 부피와 몰수의 관계를 표현한다. 온도와 압력이 같은 상황에서 기체 분자수가 증가하면 용기에 충돌하는 횟수가 증가하므로 압력이 증가한다. 하지만 외부 압력과 압력이 동일해야 하므로 용기의 부피가 증가한다. 정리해서 표현하면 같은 온도 같은 압력에서는 기체 분자수는 몰수에 비례한다.
\[V\propto n\]
아보가드로 법칙을 확장해보자. 기체는 종류에 따라 특성이 다를 수도 있지만, 물리적 특성은 비슷한 경향을 보인다. 또한, 기체의 몰수가 부피에 비례한다고 했으므로 기체의 부피가 같다면 같은 몰수가 존재할 것이다. 이를 정리하면 다음과 같은 법칙이 성립한다. ‘같은 온도, 압력, 그리고 부피에서는 기체의 종류와 상관없이 같은 몰수의 기체 분자가 들어있다.’ 다음 법칙을 1기압인 상황에도 적용하자. 기압이 1기압인 0℃에서 기체 1몰의 부피는 22.4L이다. 즉, 0℃, 1기압 22.4L에는 기체의 종류와 상관없이 기체 분자 1몰이 존재한다는 성질을 얻을 수 있다.
8. 이상기체 상태방정식
1) 개념
앞서 살펴본 보일의 법칙, 샤를의 법칙, 그리고 아보가드로 법칙을 온도, 압력, 부피, 그리고 몰을 이용해서 부피에 대한 비례관계를 표현해보자.
보일의 법칙 : \[V\propto\frac{1}{P}\]
샤를의 법칙 : \[V\propto T\]
아보가들의 법칙 : \[V\propto n\]
이상 기체의 분자들이 서로 상호작용하지 않으며, 분자들의 부피의 합이 전체 기의 부피보다 작다고 가정하자. 이때, 위의 세 법칙을 묶어 표현하면 부피에 대해 비례관계를 얻을 수 있고, 이를 기체상수 R을 이용해서 부피와 온도와 압력, 그리고 몰에 대해 등호 관계를 이용해 표현하자.
\[V\propto \frac{nT}{P}, V=R\frac{nT}{P}\]
\[PV = nRT\]
\[P : 압력, V : 부피, n : 몰, R : 기체 상수, T : 절대온도 R = 8.314J/mol K\]
2) 이상기체 방정식을 이용한 기체 분자의 몰질량 구하기
$PV=nRT$에서 기체의 몰질량(분자량)과 질량을 각각 M, w라고 하면 몰-분자량-질량 관계를 이용해서 위의 식을 정리할 수 있다.
\[n=\frac{w}{M}\]
\[M=\frac{wRT}{PV}\]
만약 기체의 밀도를 알고 있고, 이를 d라고 한다면 식을 바꿔표현할 수 있다.
\[M=\frac{dRT}{P}\]
상황에 맞추어 분자량으로 정리한 두 식을 적절히 이용한다면 이상기체 방정식으로부터 기체의 몰질량을 구할 수 있다.
9. 몰질량(분자량)
1) 개념
몰질량은 1몰에 들어있는 원자 혹은 분자의 질량을 의미한다. (몰질량)=(원자 또는 분자 1개의 실제질량)×(아보가드로수) 를 통해서 구할 수 있으며 이는 원자량 및 분자량에 g을 붙인 값과 동일하다.
2) 측정
몰질량을 측정할 수 있는 방법은 다양하다. 실제 원자와 분자 1개의 질량만 알 수 있다면 아보가드로수를 곱해서 몰질량을 측정할 수 있다. 하지만, 실제 원자 및 분자 1개의 질량을 측정하는 일은 어려운 일이므로, 이상기체 상태방정식을 이용한다면 오차는 분명히 있겠지만, 대략적인 몰질량을 측정할 수 있다. 우선 초기 플라스크와 알루미늄 뚜껑의 처음 무게를 측정하면 이는 플라스크와 알루미늄 뚜껑과 일반 공기의 무게를 측정한 수치를 알 수 있다. 그 다음 물보다 끓는 점이 낮은 액체시료를 플라스크에 넣어 중탕하고 이를 식힌 후, 플라스크의 질량을 측정하면 플라스크와 알루미늄 뚜껑 및 시료의 무게를 구할 수 있다. 두 질량의 차이를 구하면 구하고자 하는 기체의 질량 - 공기의 질량을 알 수 있다. 이때, 공기의 질량은 공기의 밀도가 제시되었다면 플라스크의 부피를 이용해서 구하고 그렇지 않다면 공기의 평균 분자량이 29인 것을 이용해서 공기의 질량을 구한다. 최종적으로 구한 실제 시료의 무게를 이상기체 방정식에 대입해서 풀이하면 해당 시료의 몰질량을 추론할 수 있다.
측정과정 중 유의해야하는 사항이 있다. 우선, 사용하는 액체 시료가 물보다 끓는점이 낮아 중탕하는 과정에서 충분히 기화되어야 액체상태로 남아있는 시료가 없어 질량을 보다 정확히 구할 수 있다. 또한, 액체 시료의 양이 충분하지 않아 플라스크 공간을 기체로 다 채우지 못한다면 실제 플라스크의 부피와 다른 부피 값을 가지므로 충분한 양의 액체시료를 준비해야 한다. 또한, 플라스크를 중탕할 때, 플라스크가 충분히 물에 잠겨야 온도가 균일하게 플라스크에 전달된다. 그래야 기체들이 같는 평균분자운동에너지가 거의 균일하며 내부 압력을 거의 균등해지는 결과에 이르기 때문이다.
Ⅳ. Chemicals & Apparatus
1. Apparatus
Hot plate 1개, 스탠드 1개, 클램프 2개, 온도계 1개, 500mL 1개, 10mL 눈금실린더 1개, 100mL 눈금실린더 1개. 100mL 둥근 플라스크 1개, 1회용 needle, 목장갑, 알루미늄 호일, 피펫
2. Chemical
Isopropyl alcohol(IPA) 몰질량: 60.10g/mol, 끓는점 82.6℃ 및 증류수
Ⅴ. Procedure
1. 깨끗하게 씻어서 말린 100mL 둥근 플라스크에 알루미늄 호일로 뚜껑을 만들어 씌우고, 바늘로 작은 구멍을 뚫는다. 이때, 구멍의 크기는 작을수록 좋다.
2. 뚜껑을 덮은 플라스크의 무게를 화학저울을 사용해서 정확하게 측정한다.
3. 플라스크에 약 3mL의 액체 시료를 넣고 뚜껑을 다시 막고, 스탠드에 고정시킨다.
4. 500mL 비커에 물을 채우고 끓을 때까지 가열한다.
5. 플라스크를 비커의 바닥에 닿지 않을 정도로 물속에 깊이 넣는다.
6. 끓는 물의 온도와 대기압을 측정하고, 플라스크 속의 액체가 모두 기화할 때까지 기다린다. 이 때, 플라스크를 절대 꺼내면 안 된다.
7. 플라스크의 액체가 모두 기화하면 잠시 기다린 후에 플라스크를 끓는 물에서 꺼내 식힌다. 플라스크가 매우 뜨거우므로 손으로 만지지 않도록 한다.
8. 플라스크 바깥에 묻은 물을 완전히 닦아낸다. 그리고 말린 플라스크와 뚜껑의 무게를 다시 측정한다.
9. 플라스크를 깨끗하게 씻은 후에 증류수를 가득 채우고, 눈금실린더를 사용해서 증류수의 부피를 측정하고 이 값을 이용해 플라스크의 부피를 계산한다.
Ⅵ. Data & Result
1. 실험결과
|
|
1회 |
2회 |
|
플라스크와 알루미늄 뚜껑의 처음 무게 (g) |
79.9167 |
79.042 |
|
식힌 플라스크와 뚜껑의 무게 (g) |
80.2640 |
79.406 |
|
응축된 시료의 무게 (g) |
0.3473 |
0.364 |
|
끓는 물의 온도 (K) |
372.5 |
371 |
|
대기압(atm) |
1 |
1 |
|
플라스크의 부피 (L) |
0.139 |
0.139 |
|
액체시료의 몰질량 (g/mol) |
76.4 |
79.8 |
2. 오차율
|
|
1회 |
2회 |
|
실제 몰질량 값 (g/moL) |
60.10 |
60.10 |
|
실험 몰질량 값 (g/moL) |
76.4 |
79.8 |
|
오차율 |
27.2 |
32.8 |
Ⅶ Discussion
이상기체 상태방정식으로 몰질량을 유도하면 다음과 같다.
\[M=\frac{wRT}{PV}\]
실험을 측정한 환경에서는 기체 상수는 상수이므로 측정값에 영향을 미치지 않는다. 실험으로 얻은 몰질량 값이 실제 몰질량보다 더 크다는 것을 감안하여 오차에 영향을 준 변수와 개선 방향을 정리하자.
|
|
변수 |
실제 값에 대한 측정 값 |
개선 방향 |
|
분모 |
V |
실제보다 작게 측정된 것으로 예상 |
증가하는 방향으로 개선 |
|
P |
|||
|
분자 |
T |
실제보다 크게 측정된 것으로 예상 |
감소하는 방향으로 개선 |
|
w |
이제 각 변수별로 오류가 난 원인을 이유를 진행된 실험 과정을 통해 분석해보고 최대한 올바르게 설계한다면 어떤 방향으로 실험 몰질량 값이 변화할지 예상해보자.
1. 부피(V)에 대한 분석
부피를 측정하기 위해 100mL 눈금실린더를 사용했다. 하지만, 부피 플라스크의 부피가 100mL보다 커서 동일한 눈금실린더를 2번 사용해야 했다. 시간상의 문제로 처음 측정했던 눈금실린더를 충분히 말리지 못하고 사용했다. 즉 2번째로 부피를 측정했을 때 기존의 액체와 중첩된 수치로 측정되어 부피가 실제보다 더 크게 측정되었다고 볼 수 있다. 또한 눈으로 부피를 측정했기 때문에 눈으로 실제 부피에 대해 오차가 발생했을 수도 있다. 만약 측정상의 오류를 개선하고 눈금실린더를 충분히 말려 측정했다면 측정수치보다 보다 작은 부피 값을 얻을 수 있을 것이라고 예상한다. 이는 실제 설계한 개선방향과는 다름을 알 수 있다.
2. 압력(P)에 대한 분석
실제 실험실 내부의 압력을 측정하지 않고 1기압으로 가정했기 때문에 오차가 발생할 수 있다. 표준 대기압이 0℃ 지구 표면에서 측정한 수치이다. 하지만, 실험실 내부의 온도가 더 크고 높이가 표면보다 높아 중력가속도의 크기다 더 작을 것이다. 그러므로 압력계를 이용해서 실제 실험실 내부의 압력을 측정한다면 1기압보다 더 작게 측정될 것이다. 이 또한 실제 설계한 계선방향과는 다르다고 확인할 수 있다.
3. 온도(T)에 대한 분석
실험과정 도중에 IPA가 충분히 기화했는지 확인하기 위해서 플라스크를 한번 꺼냈었다. 이때 순간적으로 온도가 낮아졌지만, 그 이후에도 충분히 중탕을 했기 때문에 온도에 대해서는 크게 오류가 없었다고 생각한다. 하지만, 온도의 측정 또한 직접 눈으로 했기 때문에 여기서 발생하는 오류가 있을 수 있다.
4. 질량(w)에 대한 분석
이상기체 상태방정식에 대기압, 끓는점의 온도와 플라스크의 부피를 대입하면 실제로 측정되어야 하는 IPA의 몰수를 알 수 있다. 1atm×0.137L=xmol×0.08206atm∙L/mol∙K×372.5K 이므로 $x=4.482×10^{-3}$이다. 또한 IPA의 몰질량이 60.10g/mol 이므로 실제로는 응축된 시료 무게가0.2694g이 측정되었어야 한다. 이 수치를 통해 2가지 사실을 알 수 있다. 첫번째, IPA가 기화되는 과정에서 호일에 뚫은 구멍을 통해 기체상태의 IPA가 빠져나왔음을 알 수 있다. 넣어준 액체 시료는 3mL이며 밀도는 $0.7809g/cm^3$이므로 기체상태의 시료가 온전히 다시 응축되었다면 2.4327g이 측정되었어야 하기 때문이다. 두번째로 실제 측정되어야 하는 수치보다 실험에서 측정된 질량이 더 큰 사실을 알 수 있다. 실험에서 측정한 응축된 시료의 양이 0.3473g이기 때문이다. 이렇듯 실제 수치보다 질량이 더 크게 측정되었음을 알 수 있다. 여러 요인이 있었겠지만 실험과정에서 불필요하게 응축된 액체시료가 질량이 더 크게 측정되는데 기여했다. 우선 IPA를 중탕하던 중에 시료가 다 기화했는지 확인하기 위해서 중간에 플라스크를 한 번 꺼낸 것이 문제가 되었다고 판단된다. 후에 충분한 시간을 가열했지만, 기구의 크기가 맞지 않아 플라스크를 완벽하게 끓는 물 속에 집어넣지 못했기에 플라스크의 목부분에 미처 기화되지 못한 액체시료가 남아있을 가능성이 있었다. 또한, 알루미늄 호일로 만든 뚜껑부분에도 응축된 IPA가 남아있을 수 있다. 뚜껑부분은 플라스크의 외부와 직접 맞닿아 있는 부분이기 때문에 온도차이에 의해서 IPA가 응축될 수 있기 때문이다. 액체 상태의 IPA는 기체 상태의 IPA보다 밀도가 크기에 질량이 더 크게 측정된다. 실험진행 중에 미처 파악하지 못한 응축된 시료가 질량이 더 크게 측정되는데 영향을 줬다고 파악된다.
Ⅷ. Reference
1. Brown 외 6인, Chemistry The Central Science 14th edition, Pearson, 2019, pp. 138, 440~448, 451-452, 457-459, 463-466
2. 동아출판, High Top 하이탑 고등학교 물리 2 1권, 동아출판, 2012, pp. 192~193
3. 대한화학회, 표준 일반화학실험 제 7판, 천문각, 2011, pp. 55~58
4. John R.Rumble, CRC Handbook of Chemistry and Physics 85th edition, pp.3-482
'자료.zip > 일반화학실험' 카테고리의 다른 글
| 크로마토그래피(Chromatography) (2) | 2021.02.09 |
|---|---|
| 나일론 합성 (5) | 2021.01.30 |
| 엔탈피 측정 (0) | 2021.01.28 |
| 비누 합성 (0) | 2021.01.28 |
| 아보가드로 수의 결정 (0) | 2021.01.18 |