
Ⅰ. Title
엔탈피 측정
Ⅱ. Purpose
산과 염기의 중화 반응을 이용해서 엔탈피가 상태함수임을 확인한다.
Ⅲ. Theory
1. 계(system)와 주위(surroundings)
열역학에 대해서 논의하기 위해서, 우주(universe) 전체를 고려하는 것이 아니라, 특정 부분을 고려해야 한다. 이때 우리가 관찰하고자 하는 반응이 발생하는 공간을 계(system), 우주에서 계를 제외한 나머지 부분을 주위(surroundings)라고 한다. 계는 물질과 에너지의 이동여부에 따라 3가지로 구분한다. 열린계(open system)은 계에 있는 에너지와 물질이 주위와 교환이 가능한 계를 의미한다. 뚜껑이 없는 물을 끓이는 냄비를 열린계의 예로 들 수 있다. 두 번째로, 고립계(isolated system)은 계의 물질과 에너지가 모두 주위로 이동할 수 없는 상태에 놓인 계를 의미한다. 각각의 계도 의미가 있다. 그러나, 열역학을 논의할 때 가장 중요한 계는 닫힌계(closed system)다. 닫힌계는 주위로 물질은 이동할 수 없지만, 에너지가 이동 가능한 상태에 놓인 계를 의미한다. 닫힌 계를 설정하기 위해서 압력과 부피 중 한가지를 고정하는 형태를 이용한다. 실린더를 이용하면 반응 중 압력을 대기압으로 유지할 수 있으며, 강철용기 내에서 반응을 진행하면 부피를 용기의 부피로 고정할 수 있다.
2. 내부에너지 (internal energy)
1) 내부에너지의 뜻과 의미
내부에너지(internal energy)는 계를 구성하는 모든 물질들의 운동에너지와 퍼텐셜에너지를 더한 값이다. 에너지이기에 값을 쉽게 측정할 수 있다고 생각하지만, 내부에너지는 에너지의 절대적 수치를 측정할 수 없으며, 계의 에너지 변화에 따른 변화량에 대해서만 논의 가능하다. 반응 후의 에너지를 $E_{final}$, 반응 전의 에너지를 $E_{initial}$이라고 할 때, 에너지 변화량은 $\Delta E=E_{final}-E_{initial}$이다. 에너지의 변화량을 구할 때 숫자, 단위, 그리고 부호를 이용한다. 숫자와 단위는 단순히 에너지 변화량의 절대적인 크기에 대해 논할 때만 사용한다. 하지만, 부호는 에너지가 어떠한 방향으로 이동했는지 보여준다. 만약 $\Delta E>0$이라면, $\Delta E_{final} > \Delta E_{initial}$인 것을 뜻한다. 즉, 에너지가 주위에서 계로 유입되었음을 의미하며 이러한 반응을 흡열반응(Endothermic process)이라고 한다. 반면 $\Delta E<0$이라면, $\Delta E_{final}<E_{initial}$인 것을 뜻하며, 에너지가 계에서 주위로 유출되었음을 알 수 있다. 이런 반응을 발열반응(Exothermic process)이라고 한다.
2) ΔE와 열(heat)과 일(work)사이의 관계
어떤 계에서 화학적 변화와 물리적 변화가 발생하면 변화의 결과는 열의 변화 혹은 일의 변화로 귀결된다. 이를 통해 에너지 변화량을 열의 유출입과 일의 작용대상을 관련 지어 수식으로 표현할 수 있다.
$\Delta E=q+w$(q: 계에 유출입한 에너지, w: 계에 대한 일의 작용범위)
$\Delta E,q,w$의 부호관계를 아래의 표로 정리해서 알아보자.
|
|
+ 부호 |
- 부호 |
|
q |
계가 주위로부터 열을 받음 |
계가 주위로 열을 전달함 |
|
w |
주위로부터 계가 일을 당함 (일을 받음) |
계가 주위로 일을 해줌 |
|
ΔE |
두 값의 합이 양수임을 의미하며 내부에너지가 증가함을 뜻함 |
두 값의 합이 음수임을 의미하며 내부에너지가 감소함을 뜻함 |
하나의 반응에서 $q$와 $w$의 부호가 동일할 필요는 없다. 두 값의 합으로 $\Delta E$의 크기와 부호를 결정해서 에너지가 어떤 방향으로 이동했는지를 파악할 수 있다.
3. 상태함수(State function)
상태함수는 물질의 변화 과정과 관계없이 현재 물질이 놓여있는 상태와 조건에 의해서만 정의되는 값을 의미한다. 값을 결정짓는 조건은 여러가지가 있지만 대표적으로 온도(temperature), 압력(pressure), 그리고 물질의 양 혹은 질량(quantity of mass)가 있다. 상태함수는 크기성질이기 때문에 물질의 양도 결정요인에 포함된다. 또한 물질이 고체인지, 액체인지, 그리고 기체인지인 물질의 상태도 상태함수의 값을 결정하는데 영향을 미친다.
4. 엔탈피(Enthalpy)와 반응 엔탈피(Enthalpies of Reaction)
1) 압력 크기 작업 (Pressure and Volume Work, P-V Work)
엔탈피의 보다 편한 논의를 위해서 압력 크기 작업에 대해 알아보자. 압력 크기 작업은 실린더 내부에서 반응한 기체들이 일의 결과로 기체의 팽창과 수축을 수반하는 일을 의미한다. 즉, 압력이 일정한 상황에서 기체가 하거나 받은 일을 뜻한다. $\Delta V=V_{final}-V_{initial}$이라 하고, 압력 $p$가 일정하다고 할 때, 일 $w=-p\Delta V$의 값을 갖는다. 압력은 항상 0보다 크거나 같으므로 일의 부호는 부피변화의 부호가 결정한다. 계를 실린더 내부라고 설정하고 표를 통해서 실린더의 부피 변화에 대한 $\Delta V$의 부호, 그리고 $w$의 부호가 갖는 관계성과 의미를 파악하자.
|
|
ΔV의 부호 |
w의 부호 |
계와 주위의 관계 |
|
실린더 팽창 |
양수 |
음수 |
계가 주위에 일을 함 |
|
실린더 수축 |
음수 |
양수 |
계가 주위로부터 일을 당함 (일을 받음) |
2) 엔탈피(Enthalpy)
① 엔탈피의 정의
엔탈피(H)는 내부에너지($E$)와 압력($p$), 그리고 부피($V$)를 이용해서 정의할 수 있다.
$H=E+pV$
내부에너지와 압력, 그리고 부피도 상태함수 이므로 엔탈피도 상태함수다.
② 압력 크기 작업을 적용한 엔탈피의 변화량이 갖는 의미
실생활에서 발생하는 반응은 대부분 압력이 일정한 상태에서 진행된다. 이 현상을 엔탈피에 보다 쉽게 적용하기 위해서 엔탈피의 변화량과 압력 크기 작업이 갖는 관계성을 이용한다. 일정 압력 하에서 엔탈피의 변화량은 다음과 같다.
$\Delta H=\Delta (E+pV)=\Delta E+p \Delta V$
동일한 압력 사이에서 발생하는 열의 이동량을 $q_p$라고 정의하자. 내부에너지의 변화량 $\Delta E=q_p+w$이 성립한다. 또한 압력 크기 작업에서 일을 $w=-p \Delta V$로 표현할 수 있다. 이 두 식을 엔탈피의 변화량에 대입해서 식을 정리할 수 있다.
$\Delta H=q_p+w+(-w)=q_p$
즉 엔탈피의 변화량은 압력이 일정할 때, 계가 얻거나 잃은 열의 크기를 뜻한다. 압력이 일정할 때 출입한 열의 크기를 재는 일은 비교적 용이하기에 내부에너지를 고려하지 않고도 엔탈피의 변화량을 쉽게 측정할 수 있다. $q$는 상태함수가 아니지만, 일정 압력 크기 작업에 한정해서 $q_p$는 상태함수로 볼 수 있기에 엔탈피의 변화량도 상태함수이며, 처음과 끝의 엔탈피의 수치만 비교하면 된다.
③ 엔탈피의 변화량의 부호가 갖는 의미
엔탈피 변화량의 부호가 양수이면 $q_p$도 양수이다. 이는 계가 주위로부터 열을 얻었음을 의미하므로 이 반응은 흡열반응이다. 반면에 엔탈피의 변화량이 음수를 나타낸다면, $q_p$가 음수이며 계가 주위로 열을 전달한 것이다. 이 반응의 결과로 계의 온도가 감소하므로 발열반응이다.
3) 반응 엔탈피 (Enthalpies of Reaction)
① 반응 엔탈피의 정의와 표현
엔탈피의 변화량은 다음과 같다. $\Delta H=H_{final}-H_{initial}$ 이를 화학반응으로 확장해서 적용시켜서 다음 식을 얻을 수 있다.
$\Delta H_{rxn}=H_{products}-H_{reactants}$ ($H_{products}$ : 생성물의 엔탈피, $H_{reactants}$ : 반응물의 엔탈피)
여기서 $\Delta H_{rxn}$를 반응 엔탈피라고 한다. 반응 엔탈피는 화학 반응식 오른쪽에 부호와 크기, 그리고 단위를 적어서 표현한다. 반응 엔탈피는 왼쪽의 반응이 완전히 진행되었을 때 변화하는 열의 출입량을 표현한 것이다.
② 반응 엔탈피를 이용할 때 주의사항
ⅰ) 반응 엔탈피는 크기성질이다. 그러므로 반응 계수와 반응 엔탈피의 크기는 비례한다. 즉, 반응물의 계수가 1일 때와 2일 때 반응 엔탈피의 크기는 2배 차이가 난다.
ⅱ) 역반응의 반응 엔탈피는 정반응 반응 엔탈피와 크기는 같지만 부호는 반대다. 즉, 반응을 시킬 때 필요했던 에너지의 크기는 같지만, 계와 주위에 대한 에너지 흐름의 방향은 반대가 되어야한다.
ⅲ) 반응 엔탈피는 상태함수이다. 그러므로 반응식에 적힌 물질들의 상태를 분명하게 표현해야 한다. 예를 들어 $H_2O$의 상태가 액체(l)인 것과 기체(g)인 것의 반응식은 서로 다른 반응 엔탈피 값을 갖는다. 상태함수는 물질의 상태에 의해서 값이 결정되기 때문이다.
5. 열용량(heat capacity)와 비열(specific heat)
어떤 물질이 열을 받으면 온도가 증가하는 것은 자명하다. 하지만, 물질의 종류와 상태 그리고 양에 따라서 받은 열에 대해서 온도가 변하는 양상은 다양하다. 이런 현상을 다음 두가지 형태를 통해서 설명한다.
1) 열용량(heat capacity)
열용량(heat capacity)은 어떤 물질의 온도를 1K 혹은 1℃올리는데 필요한 열의 양을 의미한다. 표기는 C로 하며, 물질의 양에 따라서 수치가 변하는 크기 성질이다. 만약 어떤 물질의 양이 1몰일 때, 1몰에 대해서 필요한 열의 양을 특별히 molar heat capacity라고 한다.
2) 비열 (specific heat)
비열(specific heat)은 열용량이 크기 성질이기에 물질의 양에 의해서 수치가 달라지는 점을 개선했다. 비열은 어떤 물질 1g의 온도를 1K 혹은 1℃올리는데 필요한 열의 양을 의미한다. 정의에서 알 수 있듯이, 비열을 물질의 양과 관계없이 정의되므로 세기 성질이다. 비열을 $C_s$라고 표현한다. 비열을 수식으로 표현하면 다음과 같고, 단위는 J/g-K 혹은 J/g-℃을 이용한다.
$C_s=\frac{q}{m \times \Delta T}$ ($q$ : 열량, $m$ : 물질의 질량, $\Delta T$ : 온도 변화량)
비열은 물질의 상태나 온도변화량을 측정하는 공간의 온도에 영향을 받지만 특정 시점의 비열은 상수이므로 식을 정리하면 열량을 얻을 수 있다.
$q=C_s \times m \times \Delta T$
비열의 값을 알고 있는 물질을 이용한다면, 온도변화를 통해서 열량을 측정할 수 있으며, 이는 엔탈피의 변화량을 측정하는데 도움이 된다.
6. 열량계의 종류 및 온도 변화의 측정
1) 일정압력 열량계 (Constant-Pressure Calorimetry)

일정압력 열량계는 용기를 완벽하게 밀폐시키지 않아서 실험 상황의 압력을 대기압으로 상정하고 실험을 진행할 수 있다. 일정압력 열량계는 계와 주위가 완벽하게 구분된 상태가 아니라 혼재되어 있는 상황을 이용한다. 반응이 일어나는 부분만을 계로 하고, 물을 포함한 나머지 부분을 주위라고 할 수 있다. 다만, 반응 중 계에서 발생한 열 출입은 주위 중 물과 관련해서 발생한다. 만약 이 반응이 흡열 반응이라 계로 열을 흡수한다면 주위에 해당하는 물은 열을 내어준다. 발열 반응이 발생할 때 계에서 방출한 열은 주위의 물로 흘러간다. 수용액의 열량을 $q_{soln}$, 반응이 일어나는 계의 열량을 $q_{rxn}$이라고 하자. 일정한 압력계에서 발생한 온도 변화이므로 $q_{rxn}=q_p$이다. 또한 수용액의 온도변화와 계의 온도변화의 방향이 서로 반대이므로 다음 관계가 성립한다.
$q_{rxn}=q_p=-q_{soln}$
따라서 일정압력 열량계에서 측정한 주위의 열량을 통해서 계의 열량을 유도할 수 있으며, 같은 압력이라는 조건 하에서 엔탈피의 변화량을 쉽게 구할 수 있다. 이번 실험에서는 밀폐된 용기를 사용하지 않는 것으로 보아 일정압력 열량계를 사용하는 것으로 볼 수 있다.
2) 일정부피 열량계 (Constant-Volume Calorimetry, Bomb calorimeter)

일정압력 열량계와는 달리 일정 부피 열량계는 반응 중 부피를 일정하게 유지하는 과정을 통해서 열량변화를 측정한다. 반응 도중에 부피가 변하면 안되므로 열량계의 통을 강철 용기와 같이 부피가 변하지 않는 용기를 이용한다. 또한 이 용기는 고압력을 버틸 수 있도록 설계되었다. 일정부피 열량계는 연소반응에 대한 정보를 측정할 때 유용하게 이용한다. 점화선을 이용해서 연소 반응을 일으키면 물을 포함한 주위의 온도가 올라간다. 열용량 혹은 비열을 알고 있는 시료를 이용하면 다음 식을 통해서 계의 열량을 구할 수 있다.
일정 압력 열량계와 일정 부피 열량계는 큰 차이가 있다. 일정 압력 열량계는 일정한 압력에서 실험을 진행했기에, 열량의 변화량을 바로 엔탈피의 변화량에 적용할 수 있다. 하지만, 일정 부피 열량계에서 구한 계의 열량은 일정한 압력이 아니기에 바로 적용이 불가능하다. 이 변화된 열량은 엔탈피의 변화량에 바로 적용되는 것이 아니라 내부에너지의 변화량을 뜻한다. 일정 부피 에서의 엔탈피 변화량은 어떠한 관계를 갖는지 살펴보자.
$\Delta H=\Delta E+\Delta (pV)=\Delta E + V\Delta p$
이때, $V \Delta p$ 값은 무시할 수 있을 만큼 작기 때문에 내부에너지의 변화량과 엔탈피의 변화량은 거의 같다고 간주할 수 있다.
$\Delta H = \Delta E$
따라서 주위의 열량 변화를 통해서 계의 열량을 구한 후, 내부에너지의 변화량과 엔탈피의 변화량 사이의 관계를 이용해서 해당 반응의 엔탈피 변화량을 구할 수 있다.
7. 헤스의 법칙 (Hess’s Law)
엔탈피와 그 변화량은 상태함수이다. 즉, 물질의 양, 물질의 상태 및 반응 처음과 후의 상태만 고려하면 된다. 또한, 반응의 과정은 어떻게 일어났는지 고려하지 않는다. 이러한 상태함수의 성질을 이용하면 독립된 반응들의 조합을 통해서 쉽게 반응시킬 수 없는 반응의 엔탈피 변화량을 다른 실험들의 측정을 통해서 간접적으로 구해낼 수 있다. 다만 헤스의 법칙을 적용할 때는 여러 주의점들을 고려해야 한다.
① 상태함수이기에 물질의 양도 고려해야 한다. 다만 반응 엔탈피에서 물질의 양은 계수가 결정하기에, 더하는 반응식들의 계수를 통일해야 한다. 이때, 계수가 변하는 반응식이 있다면 반응 엔탈피도 계수가 변화한 만큼 변화시킨 후 더해야 한다.
② 상태함수이기에 물질의 상태도 중요하다. 각각의 엔탈피의 위치를 표현할 때, 물질의 상태도 반드시 표현해야 한다.
③ 반응 엔탈피는 변화에 대해서만 논의할 수 있으므로, 절대적인 수치는 표현하지 않고, 화살표를 통해서 엔탈피의 증가량과 감소량, 엔탈피의 증가 감소를 표현한다.
이번 실험도 마찬가지로 헤스의 법칙을 적용할 수 있다. 실험 2에서 측정한 용해열과 실험 3에서 측정한 중화열을 기반으로 둘의 반응 엔탈피 변화량을 더하면 실험 1에서 구한 엔탈피 변화량을 구할 수 있다.
8. 생성 엔탈피 (Enthalpies of Formation)
1) 의미
생성 엔탈피(Enthalpies of Formation)는 안정한 원소의 상태의 물질이 화합물을 형성할 때 발생하는 반응 엔탈피 변화량을 의미한다. 이때 생성된 화합물의 양은 1몰을 기준으로 하며, 반응물은 그에 따라 계수를 맞추면 된다. 또한, 298K(25)에서 측정한 생성 엔탈피는 따로 표준 엔탈피(Standard Enthalpies of Foramtion)이라고 해서 실온에서 발생하는 엔탈피 변화량을 논의한다. 반응물에 오는 물질은 자연적으로 존재하는 상태의 물질이 반응해야 한다. 예를 들어, 기체의 경우 하나의 원자가 아닌 이원자 분자의 형태를 반응식에 표기해야 한다. 그리고 같은 생성물을 만든다고 하더라도 엔탈피가 상태함수이기 때문에, 생성한 화합물의 상태에 따라 생성 엔탈피가 변화할 수 있다.
2) 생성 엔탈피를 이용한 반응 엔탈피의 계산
반응물과 생성물의 생성 엔탈피를 고려한다면, 생성 엔탈피 값만 알고 있다면 실험을 하지 않더라도 반응 엔탈피를 구할 수 있다. 생성 엔탈피를 이용해서 반응 엔탈피를 계산할 때, 다음 과정을 따라 적용하면 된다.
① 화합물에 대해서 생성 반응인지, 분해반응 인지를 구분한다. 반응물에 들어가는 물질은 분해 반응식을 이용해야 한다. 이는 생성에 대한 역반응이므로 엔탈피 또한 크기는 같게 부호는 다르게 사용한다.
② 화학 반응식들을 모두 더했을 때, 최종적으로 처음에 구하려던 화학 반응식에 대해서 구할 수 있도록 화학 반응식의 계수를 조절한다. 이때, 계수가 변한만큼 생성 엔탈피도 변화시켜야 한다.
③ 헤스의 법칙을 이용해서 각 반응의 생성 엔탈피를 더해서 반응 엔탈피를 구한다.
위의 과정을 따라서 화학 반응들의 반응 엔탈피를 구해보면 다음과 같은 식을 얻을 수 있다.
$\Delta H_{rxn}^{\circ}=\sum n\Delta H_{f}^{\circ}-\sum m\Delta H_{f}^{\circ}$
여기서 $n$과 $m$은 계수를 전환할 때, 각각 생성물과 반응물 생성 엔탈피에 곱해지는 수를 의미한다.
9. 중화반응을 이용한 반응 엔탈피의 논의 및 주의사항
1) 반응 엔탈피의 이론적 수치
위의 내용들을 바탕으로 이번 실험에서 구하게 될 반응 엔탈피의 이론적 수치와 용해열, 중화열에 대해서 논의해보자.
① 반응 엔탈피
생성 엔탈피를 이용하기 위해서 분해 반응식과 생성 반응식을 표현하자.
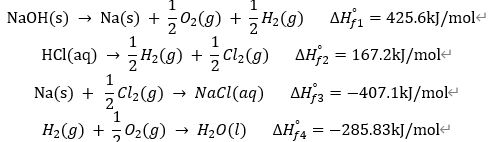
위의 엔탈피 값들과 원래 반응식을 이용해서 실제로 구해야 하는 반응 엔탈피 값을 구해보자.
\[\Delta H_f^{\circ}=\sum n\Delta H_f^{\circ} (product)-\sum m\Delta H_f^{\circ}( reactant)\]
\[\Delta H_f^{\circ}=(425.6+167.2) kJ/mol-(407.1+285.83)kJ/mol=-100.13kJ/mol\]
반응식과 엔탈피를 정리해서 표현하면 다음과 같다.
$NaOH(s)+HCl(aq)\rightarrow Nacl(aq)+H_2 O(l)\,\,\,\,\, \Delta H_1=-100.13kJ/mol$
② 중화열
중화열은 수소이온 1몰과 수산화이온 1몰이 반응할 때 형성되는 열을 의미한다. 두 강산과 강염기의 중화반응의 알짜 이온 반응식은 항상 동일하므로, 반응 엔탈피의 값도 동일하다. 반응식과 반응 엔탈피를 표현하면 다음과 같다.
$H^+(aq)+OH^-(aq)\rightarrow H_2O(aq)\,\,\,\,\, \Delta H_3=-55.83 kJ/mol$
③ 용해열
용해열은 어떤 고체 물질이 용해될 때 발생하는 열을 의미한다. 수산화나트륨은 물에 녹으면서 열을 내므로 수산화나트륨의 용해는 발열반응이다. 이때, 헤스의 법칙에 의해서 중화반응에서의 엔탈피 변화량과 용해과정시 발생하는 엔탈피 변화량의 합이 전체 반응의 엔탈피 변화량과 동일해야 한다. 헤스의 법칙을 이용해서 용해열을 계산한 다음, 반응식과 같이 표현할 수 있다.
$NaOH(s)\rightarrow NaOH(aq)\,\,\,\,\, \Delta H_2=-44.3 kJ/mol$
④ 헤스 법칙을 이용한 반응의 엔탈피 변화 표현

용해열과 중화열을 이용해서 전체 반응의 반응 엔탈피를 구할 수 있으며, 3가지 중 2가지의 수치만 알더라도 헤스의 법칙을 이용하면 나머지 반응의 반응 엔탈피 도 구할 수 있음을 알 수 있다.
2) 주의사항
실험 데이터를 추론할 때, 몇 가지 주의해야 하는 사항이 있다. 우선, 방출된 열량을 구할 때 사용하는 비열은 물의 비열이다. 열량계를 이용할 때, 반응의 열량을 바로 알 수 없기 때문에 열역학 제 1법칙을 이용해서 주위의 열량 변화를 이용한다. 수용액에서 반응이 발생하는 곳을 제외한 나머지 부분은 모두 주위로 간주하므로 물의 열량 변화를 관측하면 반응의 열량변화도 파악할 수 있다. 이때, 크기는 같지만 부호가 반대인 것만 유의하면 된다. 두 번째로 반응열은 수산화나트륨을 기준으로 진행한다. 왜냐하면 용해열에서 구할 수 있는 반응열은 수산화나트륨에 대한 용해열이 유일하기 때문에 나머지 실험에서도 수산화나트륨에 대한 반응 열을 구해주어야 헤스의 법칙을 적용할 때 오류가 없다. 마지막으로 열량을 바로 실제 수치와 비교할 수 없으므로 반응열로 수치를 변환해야 한다. 이때 2가지 사항을 고려해야 한다.
① J에서 kJ로 변화하기 때문에 수치상의 변화를 고려해야 한다.
② 1몰에 대한 수치로 통일하기 위해서 사용된 수산화나트륨의 몰을 알아야 한다. 질량을 측정하기 때문에 분자량 수치를 이용해서 몰로 환산한다. 또한, 몰 농도를 이용한 중화반응의 경우 제시된 몰 농도와 사용한 용액의 부피 값을 이용해서 사용된 수산화나트륨의 몰을 구한다.
Ⅳ. Chemical & Apparatus
1. Chemical
|
물질 이름 |
화학식 |
화학식량(g/mol) |
밀도 (g/mL) |
녹는점(℃) |
끓는점(℃) |
|
염화수소 |
HCl |
36.46 |
1.49 |
-114.22 |
-85.05 |
|
수산화나트륨 |
NaOH |
39.9971 |
2.13 |
318 |
1388 |
필요한 HCl의 종류: 0.5M HCl, 0.25M HCl
필요한 NaOH의 종류: 0.5M NaOH, NaOH(s)
증류수(H2O) 화학식량: 18.015g/mol, 밀도: 0.99707g/mL(25℃), 녹는점: 0℃, 끓는점: 100℃
2. Apparatus
100mL비커 1개, 열량계 1개, 50mL 눈금실린더 1개, 온도계, Stirring bar
Ⅴ. Procedure
실험1. ∆H1 의 측정 (반응의 전체 열량변화)
NaOH(s) + HCl(aq) → NaCl(aq) + H2O(l) ∆H1
1. 100mL 비커를 깨끗하게 씻어서 말린 후에 비커의 무게를 0.01g(소수점 아래 둘째 자리)까지 읽는다.
2. 0.25M HCl 용액 50mL를 눈금실린더로 잰 후, 비커에 넣고 열량계에 넣은 후, 열량계 구멍에 온도계를 용액에 잠기도록 꽂아 온도를 소수점 첫째 자리까지 측정한다.
3. 0.5g의 NaOH(S)를 비커에 넣고, NaOH가 다 녹을 때까지 stirring한다.
4. 용액의 온도가 가장 높이 올라갈 때의 온도를 기록하고, 비커를 꺼내서 실온까지 식힌 후 비커의 무게를 측정한다.
실험 2. ∆H2 의 측정 (용해열)
NaOH(s) → NaOH(aq) ∆H2
1. HCl 용액 대신 증류수 50mL를 사용하여 실험 1의 과정을 반복한다.
실험 3. ∆H3 의 측정 (중화열)
NaOH(aq) + HCl(aq) → NaCl(aq) + H2O(l) ∆H3
1. 100mL 비커를 깨끗하게 씻어서 말린 후에 비커의 무게를 0.01g(소수점 둘째 자리)까지 읽는다.
2. 0.5M HCl 용액 25mL를 눈금실린더로 잰 후, 비커에 넣고 열량계에 넣은 후, 열량계 구멍에 온도계를 약 17℃ 눈금 정도까지 꽂아 온도를 소수점 첫째 자리까지 측정한다.
3. 0.5M NaOH(aq) 용액 25ml를 비커에 넣고, 온도계로 온도를 측정한다.
4. 용액의 온도가 가장 높이 올라갈 때의 온도를 기록하고, 비커를 꺼내서 실온까지 식힌 후 비커의 무게를 측정한다.
Ⅵ. Data & Result
실험 1. 반응열(용해열 + 중화열)
|
비커무게 |
반응 후 비커 + 용액무게 |
용액무게 |
반응 전 온도 (℃) |
반응 후 온도 (℃) |
온도변화 |
방출된 |
반응열 |
오차율 |
|
58.11 |
106.19 |
48.08 |
21.3 |
25.1 |
3.6 |
9.0×100 |
-72.1 |
27.994 |
사용한 물질: NaOH(s) 0.5g, 0.5M HCl 50mL
방출된 열량 : $4.18J/g℃\times 18.08g\times3.6℃+0.85J/g℃\times 58.11g\times3.6℃=9.0\times 10^2J$
반응열 : $-9.0\times10^2 J\times 39.9997g,mol \times 1/0.312g\times 1kJ/1000J=-72kJ/mol$
오차율
\[\frac {-(-100.13kJ/mol)+(-72.1kJ/mol)}{100.12kJ/mol} \times 100% = 27.9994%\]
실험 2와 실험 3도 실험 1에서 진행한 연산과 같은 과정을 수행하면 그 결과를 얻을 수 있다.
실험 2. 용해열
|
비커무게 |
반응 후 비커 + 용액무게 |
용액무게 |
반응 전 온도 |
반응 후 온도(℃) |
온도변화 |
방출된 |
반응열 |
오차율 |
|
64.21 |
101.32 |
37.11 |
19.1 |
20.8 |
1.7 |
9.1 ×100 |
-45.9 |
4.3 |
실험 3. 중화열
| 비커무게 (g) |
반응 후 비커+ 용액무게 (g) |
용액무게 (g) |
반응 전 온도 (℃) |
반응 후 온도(℃) | 온도변화 (℃) |
방출된 열량 (J) |
반응열 (kJ/mol) |
오차율 (%) |
|
64.20 |
110.0 |
45.80 |
21.1 |
24.8 |
3.7. |
9.1 ×102 |
-73 |
30.06 |
Ⅶ. Discussion
1. 실험 상황에 대한 분석 및 오차 원인 분석
실험 1~3 중에서 직접 진행한 실험은 실험 2와 3이다. 실험 1을 직접 하지 않아서 결과의 신뢰성이 실험 2와 3중에서 비교적 낮다. 왜냐하면 NaOH(s)의 질량을 측정하던 상황이나 온도가 변하는 상황을 직접 관찰하지 못했기 때문이다. 또한 실험과정에 나온 대로 실험을 진행하지 않고 정량적인 수치를 일부 변형해서 실험을 진행했다. 열량은 크기 성질이므로 물질의 양에 대해서 결국 수치가 변하지만 결국 반응한 물질의 몰을 고려해서 반응열을 다시 구해 사용한 물질의 양과 관계없이 비슷한 값을 가지기 때문이다. 이 실험의 특성을 통해 실험 2를 진행할 때 정량을 NaOH(s)와 증류수를 제시된 양을 사용하지 않고 사용한 양만 정확히 측정해서 얻어내고자 하는 값을 얻을 수 있었다. 실험 진행 중 온도 변화를 정확하게 관찰할 수 없었다. 온도 변화가 생각부다 뚜렷하지 않았기 때문이다. 또한 온도의 변화가 미미하지만 오랜 시간에 걸쳐 발생했기 때문에, 그리고 온도가 가장 급변했던 순간은 반응 초기였기 때문에 최대한 정확한 값을 측정하고자 소수 첫째 자리까지 온도 변화를 측정했고 오랜 시간을 들여서 온도 변화를 관찰했다. 그리고 실험 2를 할 때, NaOH의 조해성 때문에 공기에 노출 되자마자 수분을 흡수하는 것을 관찰할 수 있었고, 이를 고려해서 약포 종이에 있는 NaOH를 최대한 넣어서 측정했던 질량과 실제 반응하는 질량의 차이를 최소화하고자 했다. 또한 반응 후 용액의 질량을 측정할 때 stirring bar의 질량을 측정하고 용액과 stirring bar의 질량을 같이 측정한 값에서 빼서 구했다.
실험상의 오차를 최대한 줄이려고 했지만, 정확한 반응열을 유도하지 못했다. 이번 실험에서 결과에 오차를 미친 요인을 크게 2가지로 구분할 수 있다. 첫 번째로 이론적으로 설계한 상황과 실제 실험을 진행한 실험실의 상황이 다르기 때문에 오차가 발생했다. 이론값을 구하기 위해서 적용한 표준 생성 엔탈피는 계가 1기압을 유지하고 25℃일 때를 기준으로 반응 엔탈피를 구한 것이다. 하지만, 압력계 내부 압력이 정확히 1기압이라고 보장할 수도 없으며, 압력계의 온도 또한 정확히 25℃가 아니다. 측정하는 계의 온도가 기준과 다를 때 엔탈피의 변화량이 매우 크지는 않지만, 오차를 내는 데에 기여할 수 있다. 또한, 실험과정 중 압력계의 미세하게 온도가 바뀌었을 것이다. 실험에서 고립계를 가정하고 실험을 진행한다. 하지만, 실제로는 에너지의 유출입이 있는 닫힌계에서 반응이 발생한다. 즉 용해나 중화반응 들이 발생할 때 계의 온도가 변할 수 있음을 의미한다. 계의 온도변화는 정확한 반응 엔탈피의 측정을 방해한다.
이론과 실험상황의 어쩔 수 없는 차이가 엔탈피 측정에 영향을 미칠 수 있음을 살펴보았다. 다음으로는 측정 과정 중 발생할 수 있는 오차에 대해 알아보자. 열량계를 계를 보고 내부에서 온도가 변한 물질들의 열량을 모두 더하므로, 물과 비커의 열량을 모두 고려해야 한다. 이를 이용해서 반응열을 구할 때 미칠 수 있는 변수들에 대해서 살펴보자.
\[\Delta H_{rxn}=\frac{C_{s,water}\times m_{soln}\times \Delta T+C_{s,beaker}\times m_{beaker}\times \Delta T}{n_{NaOH}}\]
이때, 실험 2와 실험 3의 사용된 NaOH의 몰수를 구하는 방법이 다르다.
실험 2 : $n_{NaOH}= \frac{w}{M}$ ($w$ : 질량, $M$ : 분자량)
실험 3 : $n_{NaOH}=C\times V$ ($C$ : 몰 농도, $V$ : 사용한 수용액의 부피)
위의 식들 중에서 오차가 날 수 있는 변수는 $m_{soln}, m_{beaker}, ΔT, w_{NaOH}, V_{NaOH}$이다. (더 정확하게 고려하자면 NaOH 수용액과 HCl 수용액을 제조할 때도 오류가 날 수 있지만, 제공받은 수용액의 몰 농도는 정확했다고 가정하고 논의하자. 사용했던 측정 도구는 전자저울, 메스실린더, 온도계 이므로 각 변수와 측정 도구를 연결해서 어떤 점에서 오류가 발생할 수 있었는지 살펴보자.
1) $m_{soln}$을 측정할 때는 2가지의 문제점을 찾을 수 있다. 우선 저울이 완벽한 평형 상태에 놓이지 않은 것이 질량 측정을 하는데 방해가 된다. 실험을 위해서 최대한 평형을 맞추고, 최대한 저울 정가운데에 비커를 두어 최대한 영향이 없도록 조정했지만 어쩔 수 없는 환경과 실험을 1번만 진행했기에 정확한 측정값을 기대하기 어렵다. 두 번째로 비커가 완벽하게 식었는지를 확인하지 못한 점이 질량을 측정하는데 오차가 날 수 있도록 기여했다. 이번 실험의 반응은 모두 발열 반응으로 열을 방출한다. 방출한 열이 비커에 열을 가해 비커 또한 온도가 변한다. 비커는 열을 받으면 팽창하는 성질이 있기 때문에 완벽하게 비커를 식히지 않는다면 용액과 비커의 질량 합에서 비커의 질량을 빼더라도 정확한 용액의 무게를 측정할 수 없다.
2) $m_{beaker}$을 측정할 때도 2가지 문제점을 찾을 수 있다. 첫 번째로 msoln을 측정할 때와 마찬가지로 저울을 완벽한 수평 상황에서 측정하기 힘들기 때문에 어쩔 수 없이 질량 측정 시 오차가 발생할 수 있다. 그리고 2번의 실험에서 같은 비커를 사용한 것이 오차가 발생하는데 기여했을 것이다. 먼저 진행한 실험 3에 대해서 크게 적용되지 않는다. 하지만, 비커를 씻고 말린 후 다시 사용한 실험 2의 경우에 문제를 일으킬 수 있다. 비커를 씻고 말렸음에도 불구하고 드라이기에 의한 부피 변화가 발생했을 수도 있고, 아세톤을 이용해서 씻는 과정도 없었으므로 물로 충분히 씻었지만 실험 3에서 반응했던 물질이 일부 남아있을 수도 있었다. 이를 무시하고 실험 2와 3의 비커의 질량을 거의 동일하게 보고 실험을 진행했기에 오류가 발생할 수 있다.
3) ΔT를 측정할 때도 마찬가지로 2가지 문제점을 찾을 수 있다. 우선 도구의 수준 부족을 문제점을 들 수 있다. 이번 실험에서 사용한 온도계는 1℃ 단위 까지만 눈금이 표현되어 있다. 하지만 실험에서 요구한 것은 0.1℃ 단위의 측정이었다. 이는 도구에 의존하지 않고 사람의 어림 짐작으로 눈금을 나누어서 측정했어야 했다. 최대한 눈금을 나누어서 측정해도, 사람의 주관이 들어가기 때문에 정확한 측정을 기대하긴 어렵다. 눈으로 측정해야 하는 도구와 부족한 단위 표현 때문에 실제 갑보다 부정확한 값을 측정했을 것이라고 예상한다. 또한, 반응이 정확하게 완료되는 시점을 모르기 때문에 언제까지 측정을 계속 해야 되는지 모르는 것이 온도 변화량을 부정확하게 측정하는데 영향을 미쳤을 것이다. 중화반응과 용해반응 모두 반응이 종료된 시점에서 온도가 제일 높다. 하지만 사용한 시료들에 대해서 언제 반응이 종료되는지를 몰랐으며 반응속도에 대한 정보도 없었다. 결국 정확하게 반응이 언제 종료되었는지를 알 수 없었기에 최고 온도를 측정해야 하는 정확한 시기를 알지 못했다. 최고 온도를 정확히 측정하지 못해서 온도 변화량을 정확하게 구하지 못했다. 위의 2가지 원인과는 별개로 실험 2를 진행할 때는 또다른 오차 원인이 존재한다. 수산화나트륨의 조해성을 원인으로 들 수 있다. 수산화나트륨의 조해성 때문에 증류수에 넣기 전에 이미 일부는 대기 중의 수증기와 반응해서 액체로 변해 있었다. 사용했던 모든 수산화나트륨에 대한 용해열을 측정하지 못했고 일부에 대해서만 측정이 가능했기에 오차가 생겼다고 생각한다.
4) $w_{NaOH}$는 2가지 이유 때문에 정확히 측정되지 못했다. 앞서 저울을 이용했던 변수들의 오차 원인과 같이 완벽하게 수평 상황에서 질량을 측정할 수 없다는 점을 첫 번째 이유로 들 수 있다. 두 번째로 수산화나트륨이 갖는 특별한 성질인 조해성 때문에 초기에 주위에서 측정했던 질량과 계에서는 다른 양이 용해되었을 것이다. 앞서 온도변화에 영향을 미쳤던 것과 유사하게, 저울이 매우 가까이 있지 않았기에 고체 상태의 수산화나트륨은 공기 중의 수증기와 반응할 수밖에 없다. 최대한 모든 양의 수산화나트륨을 사용하고자 했으나 이미 액체가 되어 약포에 붙은 수산화나트륨은 사용할 수 없었기에 측정했던 양보다 더 적은 양이 계에서 용해되었을 것이다.
5) $V_{NaOH}$는 2가지 방향으로 오차가 발생한다. 이 오차는 각각 부피를 측정하는 순간의 오차와 반응 중 생기는 오차를 의미한다. 먼저 부피를 측정하는 순간에 발생하는 오차에 대해서 살펴보자. 이번 실험에서 부피의 측정은 메스실린더를 이용했다. 메스실린더를 이용해서 측정하더라도 결국 눈으로 측정하는 것이 된다. 정확하게 측정하고자 하지만 눈으로 측정하는 이상 어쩔 수 없는 오차가 발생할 수밖에 없다. 그리고 반응에서의 오차에 대해 살펴보자. 실험 과정 중 액체를 옮기는 데에 피펫을 사용하지 않고 메스실린더에서 바로 비커로 액체를 옮겼다. 메스실린더의 크기가 크기 때문에 피펫을 사용하기 어려웠기 때문이다. 피펫을 이용해서 액체를 옮기더라도 어쩔 수 없는 오차가 발생하지만, 사용하지 않았을 경우에는 마지막까지 남은 액체를 모두 옮기기 어렵다. 결국 측정했던 부피보다 더 적은 양의 수산화나트륨 수용액이 반응한다.
앞선 오차들에 대한 분석과는 별개로 실험 1은 직접 진행한 것이 아니라 옆의 조의 데이터를 받아서 분석한 것이다. 그러므로 실험에 대한 상황을 정확하게 파악할 수 없기에 이도 정확한 측정값을 얻지 못하는 데 기여했다.
2. 생각해볼 사항
1) 실험 결과로부터 실험 1의 반응열이 실제로 실험 2와 실험 3의 반응열의 합과 동일한 값인지를 확인해본다.
전체 실험의 반응열 ΔH1=-72.1kJ/mol, 전체 실험의 반응열 ΔH2=-45.9kJ/mol, 전체 실험의 반응열 ΔH3=-73kJ/mol이다. 이때, ΔH2 + ΔH3 = -45.9kJ/mol + (-73kJ/mol) = -118.9kJ/mol이므로 a과 ㅁ는 같지 않음을 확인할 수 있다.
2) 만약 실험 1의 반응열이 실제로 실험 2와 실험 3의 반응열의 합과 동일한 값이 아니라면 그 이유는 무엇이겠는가?
이 질문에 대한 답은 앞선 discussion-1에서 언급했던 것과 같이 이상적인 상황에서 실험을 진행하지 못했다는 점과 측정상에서 어쩔 수 없는 오류가 발생한다는 점이 오차원인으로 작용했다. 더불어 세 실험을 모두 진행하지 않고 각각의 실험을 나누어서 진행했기에 결과가 더 부정확하게 측정되었다고 생각한다. 만약 실험이 완벽하게 이루어져 반응열을 정확하게 구했다면 헤스의 법칙에 의하여 실험 1의 반응열은 실험 2와 실험 3의 반응열의 합과 동일한 값을 가져야한다.
3) 실험 3에서 일어난 반응의 이온 방정식과 알짜 이온 방정식을 써보아라.
이온 반응식: Na+(aq) + OH-(aq) + H+(aq) + Cl-(aq) → Na+(aq) + Cl-(aq) + H2O(l)
알짜 이온 반응식: H+(aq) + OH-(aq) → H2O(l)
알짜 이온식을 통하 강산과 강염기가 반응할 때 수소이온과 수산화이온이 각각 1몰씩 반응한다면 그 반응열은 항상 동일함을 알 수 있다.
Ⅷ. Reference
1. 대한화학회, 표준 일반화학실험 제 7판, 천문각, 2011, pp. 103~110
2. John R.Rumble, CRC Handbook of Chemistry and Physics 85th edition, pp. 5-103
3. Brown 외 6인, Chemistry The Central Science 14th edition, Pearson, 2019, pp. 207~234, 1131~1135
4. 이희나, EBS 수능개념 이희나의 똑 소리나는 화학2, 한국교육방송공사, 2017, pp. 64
'자료.zip > 일반화학실험' 카테고리의 다른 글
| 크로마토그래피(Chromatography) (2) | 2021.02.09 |
|---|---|
| 나일론 합성 (5) | 2021.01.30 |
| 비누 합성 (0) | 2021.01.28 |
| 몰질량 측정 (0) | 2021.01.19 |
| 아보가드로 수의 결정 (0) | 2021.01.18 |