아보가드로 수의 결정

 

 

Ⅰ. Tilte

아보가드로 수의 결정

 

Ⅱ. Purpose

물 위에 생기는 기름막을 이용해 몰 단위인 아보가드로 수를 결정한다.

 

Ⅲ. Theory

1. 극성여부와 용해도의 관계

극성과 용해도를 연관지어 설명하기 위해서 엔탈피 변화를 적용해보자. 용해 현상은 크게 3단계를 거처 발생한다.

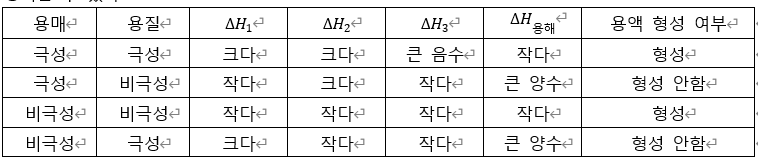
① 뭉쳐서 존재하던 용질이 각각의 분자로 분리된다. 이 과정에서 변화하는 엔탈피 변화량을 ∆H1 이라 하자. ② 용매가 용질이 들어올 수 있도록 충분한 거리로 벌어진다. 이 과정에서 변화하는 엔탈피 변화량을 ∆H2 라 하자. ③ 용매와 용질이 서로 상호작용을 한 결과 용액이 형성된다. 이때 변화하는 엔탈피 변화량을 ∆H3 라고 하자. 이 과정에서 출입한 에너지의 결과 형성된 엔탈피 수치를 용해열이라고 하며 이는 ∆H용해=∆H1+∆H2+∆H3 와 같다. 보통의 경우 ①, ②과정은 무질서도가 증가하는 과정이기에 에너지를 흡수하는 흡열 과정이고 엔탈피 변화량을 양의 값을 갖는다. 이에 반하여 과정 ③은 용질과 용매가 서로 상호작용을 통하여 안정해지는 과정이기에 엔탈피 변화의 부호는 음의 값을 갖는다. 만약 용매와 용질의 극성여부가 동일하다면 쌍극자-쌍극자 힘 혹은 분산력 사이의 힘때문에 ∆H3 의 값이 비교적 커 ∆H용해 의 값이 감소해서 용액이 형성되기에 쉬운 환경이 생성된다. 하지만, 용매와 용질의 극성이 다르다면 과정 ③에서 작용하는 분자사이의 힘의 영향력이 감소하므로 ∆H3 의 값이 매우 작아져 ∆H용해 의 값이 증가해 열을 가하는 등 상황을 변화시키지 않으면 용해현상이 쉽게 발생하지 않는다. 이러한 현상을 일컬어 극성여부와 용해도 사이에는 ‘끼리끼리 녹는’현상이 발생한다. 앞서 표현한 과정들을 정리해서 다음과 같은 표로 정리할 수 있다.

2. 스테아르 산의 단분자층 형성

Theory 1을 통해, 어떤 용매에 대해 같은 극성을 띠는 물질끼리 잘 섞이는 것을 알 수 있다. 하지만 한 물질에 극성을 띠는 부분과 띠지 않는 부분이 모두 존재한다. 이러한 물질을 계면활성제라고 일컫는다. 계면활성제는 물에 잘 녹지 않는 화합물을 물에 섞이게 하는 장점이 있다. 계면활성제를 물에 도포하면 극성을 띠는 부위는 수면에 가까이 가고 이 부위를 친수성 부위라고 한다. 또한 극성을 띠지 않는 부위는 수면과 멀리 하는데 이러한 부위는 소수성 부위이다. 이런 현상을 보여주는 물질은 인지질, 세제 등이 있지만 이번 실험에서 사용되는 스테아르 산을 이용해서 설명해보자.

위 그림의 스테아르 산의 분자구조이다. 이를 시성식으로 표현하면 CH3(CH2)16COOH이다. 이는 탄화수소 사슬에 카복실기(-COOH)가 붙은 구조임을 표현해준다. 탄화수소 사슬은 대표적을 비극성을 띠는 물질이며 카복실기는 극성을 띠는 물질이다. 스테아산 자체는 고체물질 이므로 다른 유기용매와 섞어 수면위에 도포한다면 친수성 부위인 카복실기는 수면을 향하여, 탄화수소 사슬은 수면에 반하여 정렬되어 단분자층을 형성한다. 이때, 형성된 막을 단층막이라고 한다.

 

3. 단면적의 이해

1) 단면이 원인 경우: 형성된 단면의 반지름이 r이라고 할 때, (단면적의 넓이)=πr2 이며 비교적 간단하게 구할 수 있다,

2) 단면이 타원인 경우: 단면이 타원이라고 판단되는 경우 그 넓이는 장축과 단축의 길이를 구해야 단면적의 넓이를 구할 수 있다.

왼쪽의 타원의 방정식을 $x^2/a^2+y^2/b^2=1$ 라고 하자. 이때 타원의 장반경을 a, 타원의 단반경을 b라 할 수 있으므로 (타원의 넓이) = $\pi$ab이다.

<증명>

매개변수 관계를 이용하면 $x=acos\theta$, $y=bsin\theta$ 를 얻을 수 있다. 타원의 제 1사분면에 해당하는 넓이를 A라고 하면, 아래의 식으로 표현할 수 있다. 

$A=\int_{0}^{a}ydx = \int_{0}^{\frac{\pi}{2}}\frac{1-cos2\theta}{2}=\frac{\pi}{4}ab$

(타원의 넓이) = $4A=\pi$ab

4. 동위원소와 평균 원자량

원자번호는 양성자수에 의해 정의된다. 핵분열과 핵융합을 하는 경우를 제외하고 양성자수가 변하는 일은 거의 드물기 때문이다. 하지만, 전자와 중성자수는 그렇지 않다. 같은 원소인 경우에도 상황에 따라 그 개수가 변하기 때문이다. 특히, 같은 원소이기에 양성자수는 같지만 중성자수가 다른 경우가 존재한다. 이러한 원소를 동위원소라고 한다. 동위원소는 같은 원소이지만 질량수가 다른 원소이므로, 원소의 원자량을 결정하는데 영향을 끼친다. 이렇듯 동위원소의 존재를 고려해 원소의 원자량을 구한 것을 ‘평균 원자량’이라고 한다. 평균 원자량은 각 동위원소의 원자량에 존재비를 곱한 값의 총 합으로 구할 수 있다.

 

5. 용액

용액(solution)은 용매와 용질이 균등하게 섞인 상태를 의미한다. 용액의 상태는 액체를 비롯해 고체나 기체상태일 수도 있다. 그 중에서도 이 실험과 관련된 물을 용매로 하는 용액, 즉 수용액에 대해서 보다 자세히 알아보자. 용액을 정확하게 이용하기 위해서, 용액의 농도를 정확히 해석할 수 있어야 한다.

1) 질량 백분율(퍼센트 농도)는 용액과 용질의 비율을 이용해서 정의한다.

(질량백분율)=용질의 질량용액의 질량×100%, 단위(%)

2) 몰 농도(molarity)는 용액의 부피로 혼합된 용질의 몰 수를 알 수 있고, 다음과 같이 정의한다.

(몰 농도) = 용질의 몰수mol용액의 부피L, 단위(mol/L 또는 M)

하지만, 몰 농도를 사용할 때, 두가지를 유념해야 한다. 우선, 몰 농도를 표기하는 용액을 만들 때 용액의 형성 순서에 유의해야 한다. 몰 농도는 용액의 부피를 고려해야 한다. 이때 용액은 용매와 용질을 모두 포함하기 때문에 각각의 용질과 용매의 자체적인 부피도 고려해야 한다. 그러므로 부피를 측정할 수 있는 용기에 용질을 먼저 넣고 용매를 넣어 부피를 맞추어야 정확하게 용액의 부피를 계산할 수 있다. 또한, 몰 농도는 온도에 영향을 받음을 알아야 한다. 용액의 부피는 주변환경의 온도에 따라 팽창 및 수축이 일어날 수 있다. 이는 농도 변화에 영향을 끼치므로 용액을 형성할 때 주변 실온을 고려해야 하며, 미리 용액을 만들었다면 만든 상황의 온도를 표기해야 한다.

3) 몰랄 농도()는 용매의 질량으로 용질의 몰 수를 알 수 있고, 다음과 같이 정의한다.

몰랄농도=용질의 몰수mol용매의 질량g,단위mol/g또는m

몰랄 농도는 온도에 관계없이 정의되며, 온도가 변하더라도 농도가 변하지 않으므로, 비교적 균일하게 농도 수치를 해석할 수 있다.

 

6. 몰과 아보가드로 수

1) 개념: 각각의 분자는 크기가 매우 작기에 따로 해석하기가 곤란한 상황이 많다. 이는 예전부터 과학자들에게도 고려되던 부분이었다. 그래서 수많은 원자, 분자들을 편하게 세기 위해서 ‘아보가드로 수’를 정의했다. 초기에는 수소나 산소를 기준으로 아보가드로 수를 설정했지만, 여러 오차가 발견되어 현재에는 탄소를 기준으로 아보가드로 수(Avogadro’s number)와 몰(mole)을 정의한다. 1몰은 12C 12g에 들어있는 탄소 원자의 수를 의미하며 이는 6.02214× 1023과 같다. 이때, 6.02214× 1023를 아보가드로 수라고 한다.

* 탄소를 이용해서 서술하는 방법은 수정되었으며, 현재는 아보가드로수를 그냥 하나의 상수로 정의한다.

2) 아보가드로수의 측정: 과거부터 아보가드로 수를 측정하는 다양한 방법이 고안되었다. X선을 다이아몬드에 쪼여 발생하는 회절 무늬를 분석해서 탄소 사이의 거리를 직접 측정하고 이를 바탕으로 아보가드로 수를 구할 수 있다. 또한, 브라운 운동을 통해 미세한 입자의 운동을 분석하는 방법, 콜로이드의 침강 평형 원리를 이용해 물 위의 기름의 두께로부터 원자의 크기를 추론하고 이를 바탕으로 아보가드로 수를 결정짓는 방법 등이 있다. 그 중에서도 이번 실험은 원자 하나의 실제 수치와 타 물질 사이의 관계를 이용해서 아보가드로 수를 추론한다.

고등학교 화학1 과정 중 원자량에 대해 공부를 하면 ‘원자량g=원자 1개의 실제 질량× 아보가드로 수’라는 식을 배울 수 있다. 하지만 이 식을 이용하려면 1개의 실제 질량을 측정해야 하는데, 이는 어려움이 있으므로 유사한 관계를 이용해서 아보가드로 수를 추론한다.

탄소 원자(12C) 1몰이 차지하는 부피를 Vm, 탄소 원자 하나가 차지하는 부피를 V1, 그리고 아보가드로 수를 NA라고 하면 다음과 같은 식을 얻을 수 있다.

\[N_{a}=\frac{V_{m}}{V_{1}}\]

그러므로, 아보가드로 수를 추론하기 위해서 필요한 값은 V1, 그리고 Vm이다.

① V1을 직접 구하기에는 어렵기에 사슬모양 탄화수소인 스테아르 산을 이용해서 간접적으로 그 수치를 구한다. 실험에서 사용한 스테아르 산 용액의 농도와 한방울의 부피를 구하여 포함된 스테아르 산의 질량을 구할 수 있다. 또한 2주차 실험에서 진행했던 방식과 동일하게 조사한 스테아르 산의 밀도를 이용해서 부피도 구할 수 있다. 형성된 단분자층이 스테아르 산으로 빽빽하게 구성되며 직육면체 모양이라고 가정했을 때, 형성된 단분자층 모형은 다음과 같다.

 

다음 직육면체에서 밑면이 형성된 단분자층의 면적이고, 가정에 의하여 높이는 하나의 스테아르 산 분자의 길이다. 이를 수식으로 표현하면

(스테아르 산의 부피)=(스테아르  산 분자의 길이)×(단분자층의 면적)

임을 알 수 있다. 면적의 값을 구하고 앞서 구한 부피값을 이용하면 스테아르 산 분자의 길이를 알 수 있다.

완벽한 막대기 구조는 아니지만, 계산상의 편의를 위하여 18개의 탄소 원자가 막대기 모양으로 있다고 하자. 그러면 탄소 원자 1개의 반지름 길이를 추론할 수 있으며, 탄소원자를 정육면체 모양으로 간주하고 부피를 구하면 V1을 구할 수 있다.

② 마찬가지로 Vm을 바로 구하기에는 어려움이 있다. 그래서 탄소로만 구성된 탄소 동소체 중 밀도가 가장 커 오차가 가장 적은 다이아몬드를 이용해서 탄소 원자 1몰의 부피를 추론한다. 탄소의 평균 원자량이 12.011g/mol, 다이아몬드 밀도가 3.51g/cm3임을 이용하면 다음 식이 성립한다.

(탄소의 몰부피) = (탄소의 평균 원자량)/(다이아몬드의 밀도)

\[=\frac{12.011g}{1mol}\times\frac{1cm^{3}}{3.51g}\times\frac{1mL}{1cm^3}=3.42mL/mol\]

 

 

Ⅳ. Chemicals & Apparatus

1. Apparatus

큰 물통, 눈금 실린더 10mL, 유리 모세관 피펫, 시약주걱, 삼각플라스크, 자, 공학용 계산기

2. Chemicals

헥세인(Hexane), 스테아르 산(Stearic acid), 송화가루

 

Ⅴ. Procedure

1. 피펫(pipette)을 헥세인(Hexane)으로 여러 번 닦아준다.

2. Hexane을 10mL 눈금 실린더에 방울 수를 세면서 1mL를 채운다 (pipette의 보정)

3. 대야 안에 반 이상 물을 채운 후, 잠잠해질 때까지 기다린 다음, 가운데에 송화가루를 작은 spatula로 조심스럽게 한 숟가락 뿌려준다. (spatula 작은 부분으로 한 스푼 정도 넣는데, 너무 넓게 퍼지지 않도록 주의한다.) 이때, 송화가루가 벽면에 닿지 않도록 주의해야 한다.

4. 물 위에 퍼진 송화가루 위로, pipette을 수직으로 하여 시료용액을 한 방울 떨어뜨린다.

5. 10초 정도 후, 시료용액의 직경이 일정해지면 그 직경을 측정한다. 이때 형성된 시료용액의 직경의 모양에 따라 3가지 방법이 존재한다. 1) 완벽한 원인 경우 지름을 측정한다. 2) 타원인 경우에는 타원 공식을 이용해서 구한다. 3) 원형이 아닌 경우에는 대각선을 여러 번 측정해서 평균값을 얻는다.

6. 3~5의 과정을 3번 반복하여 단면적의 평균값을 얻는다.  

 

Ⅵ. Data & Result.

1. 피펫(pipette)의 보정

1mL에 해당하는 Hexane의 방울 수: 69방울, (한 방울의 부피)=1/69 mL

2. 시료 용액 한 방울의 직경

 

3. 아보가드로 수의 추론

아보가드로 수를 추론하기 위해서는 몇 가지 가정이 필요하다. 현재 설정한 가정은 후에 실험결과로 계산한 아보가드로 수의 수치가 보통 알려져 있는 아보가드로 수치와 차이나는 요인으로 작용한다.

가정 1. 헥세인의 휘발성에 의해 시간이 흐르면 헥세인 분자들은 공기중으로 날아간다. 따라서, 스테아르 산이 용질으로 한 헥세인 용액에는 스테아르 산이 빽빽하게 있다.

가정 2. 탄소원자를 포함한 모든 원자의 모양은 완벽한 구형이다.

가정 3. 스테아르 산을 구성하는 모든 원자는 결합길이를 모두 무시한다. 즉, 오른쪽 그림과 같이 모든 원자가 완벽하게 붙어있는 상황을 상정한다. 또한, 스테아르 산을 구성하는 있는 탄소들은 모두 같은 평면에 있다.

가정 4. 형성된 단층막은 모두 소수성 부위인 탄화수소 사슬로 형성되어 있다. 초기에 형성된 모양은 완벽한 직육면체가 아니다. 스테아르 산의 구조 때문에 옆면과 밑면 등이 굴곡진 모양일 것이다. 이 도형의 부피를 완벽하게 구할 수는 없지만, 카발리에의 원리를 이용한다면 비교적 오차를 최소화하고 값을 도출할 수 있다. 초기에 형성된 단층막의 부피를 수평으로 바라보면 그림의 왼쪽에 해당하는 모양과 비슷할 것이다. 하지만, 카발리에 원리에 따라 도형을 직육면체처럼 변형하더라도 단면적이 일정하고 높이가 일정하기 때문에 그 부피는 동일하다.

위의 원리를 따라 형성한 직육면체의 높이는 초기 형성된 부피에서 생각해야 한다. 앞선 가정들에 따라 초기에 형성된 도형 중 옆면의 탄소의 일부를 확대해서 해석하자.

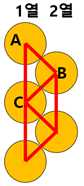
다음과 같이 지그재그로 있는 탄소 원자들의 중심을 이으면 왼쪽의 그림과 같은 모형을 얻을 수 있다. 동그라미들을 탄소원자라고 했을 때, 중심들을 이으면 삼각형 ABC와 같은 서로 합동인 삼각형들을 얻을 수 있다.  스테아르 산 하나에 포함된 탄소는 18개이므로 1열의 탄소원자의 중심을 세로로 잇고, 2열의 탄소원자의 중심도 같은 과정을 통하면 각각 9개와 8개의 세로선을 얻을 수 있다. 형성된 스테아르 산의 부피의 높이는 더 많은 세로선에 의해 결정되므로 선분AC의 길이의 9배에 해당하는 길이가 변형한 직육면체의 높이임을 알 수 있다.

위의 가정 4개를 설정하고 탄소 한 분자의 부피와 탄소의 몰 부피를 구해 아보가드로 수를 추론하자.

1) 탄소 한 분자의 부피 $V_{1}$

- 실험에 사용한 스테아르 산의 농도 : $2.00\times10^{-2} g/mLhexane$

- hexane 한 방울에 들어가있는 스테아르 산의 무게

\[\frac{2.00\times10^{-2}g}{1mL}\times\frac{1mL}{69}=\frac{2.00\times10^{-2}}{69\times9.41}g\]

- 스테아르산의 부피

\[\frac{2.00\times10^{-2}g}{69}\times\frac{1cm^3}{9.41\times10^{-1}}=\frac{2.00\times10^{-1}}{69\times9.41}g\]

- 스테아르산의 길이 $l_{s}$

\[\frac{2.00\times10^{-1}}{69\times9.41}cm^3\times\frac{2}{2.5cm^2}=\frac{2.00\times10^{-1}}{69\times9.41\times2.5}cm\]

- 탄소 원자의 반지름 길이 $r_{c}$

탄소 원자 하나의 반지름(rc )를 구하기 위하여 앞서 살펴봤던 가정 4의 삼각형 ABC를 살펴보자.

선분 AB와 선분 BC는 탄소원자의 중심을 이은 것이므로 길이는 2rc 이며 삼각형 ABC는 이등변삼각형임을 알 수 있다. 또한, 점 B에서 AC에 수산의 발 M을 이으면 각AMB는 수직이며 삼각형ABM에 대해 삼각비를 활용할 수 있다. 스테아르 산의 탄소들은 모두 단일결합을 하므로 각각의 결합각은 109.5° 이다. 이를 통해 각ABM의 크기는 54.75° 이다. 그리고, 선분AC의 길이는 $\frac{l_{s}}{9}$ 이므로 선분 AM의 길이는 $\frac{l_{s}}{18}$이다.

위의 정보를 종합하여 $r_{c}$를 구해보자.

삼각형 AMB에 대하여

\[sin54.75^{\circ}=\frac{\frac{l_{s}}{18}}{2r_{c}}\] 이므로 \[r_{c}=\frac{l_{c}}{36\times\sin54.75^{\circ}}\]

앞선 Theory에서 탄소를 정육면체로 보고 부피를 계산한다고 했지만 가정 2에서 모든 원자를 구형으로 본다고 했기 때문에 구의 부피공식과 유효숫자를 고려해서 $V_{1}$을 구할 수 있다.

\[V_{1}=\frac{4}{3}\pi r_{c}^{3}=3.1\times10^{-16}\]

2) 탄소 1몰의 부피 $V_{m}$

Theory에서 밝혔듯 탄소로만 구성된 탄소 동소체 중 밀도가 가장 커 원자사이의 거리가 가장 가까운 다이아몬드의 밀도를 이용하면 최대한 오차를 줄이고 탄소 원자 1몰의 부피를 구할 수 있다.

\[V_{m}=\frac{12.011g}{1mol}\times\frac{1cm^3}{3.51g}=3.42cm^3/mol\]

1)과 2)에서 얻은 결과를 종합하면 아보가드로 수를 얻을 수 있다.

\[N_{A}=\frac{V_{m}}{V_{1}}=\frac{3.42cm^3/mol}{3.1\times10^{-16}}=1.1\times10^{16}/mol\]

3) 오차율

알려져 있는 아보가드로 수와 우리가 직접 계산한 아보가드로 수의 비교를 통해서 오차율을 계산해보자.

(오차율) = $\frac{1.1\times10^{16}-6.02\times10^{23}}{6.02\times10^{23}}\times100=-1.0\times10^{-2}%$

Ⅶ. Discussion

실험결과로 나온 아보가드로 수치의 오차원인을 분석하기 위해 아보가드로 수를 구하는데 기인한 변수와 상수를 구분해서 식으로 표현하자.

아보가드로 수를 결정짓는 변수는 1mL의 방울 수, 단면적의 넓이가 있다. 또한, 탄소원자 하나의 반지름을 구할 때, 상정한 가정에 따라 스테아르 산의 길이에 대한 계수가 바뀌므로 이도 변수에 해당한다. 이 세 변수를 각각 $B_{h}, S_{h}, W_{h}$라고 표현하고, 상수에 해당하는 값을 모두 1로 변환해서 앞서 아보가드로 수를 구하는 과정을 반복하면 다음과 같은 비례관계를 표현할 수 있다.

\[r_{c}=\frac{l_{c}}{36\times\sin{54.75^{\circ}}}\]

$W_{h}=\frac{1}{36\times\sin{54.75^{\circ}}}$

\[N_{A}\propto(\frac{B_{h}\times S_{h}}{W_{h}})^3\]

이번 실험의 결과값이 실제 아보가드로 수보다 작았으므로, 각 변수가 가졌던 오류와 실제 수치로의 개선 방향을 다음 표를 통해서 비교해보자.

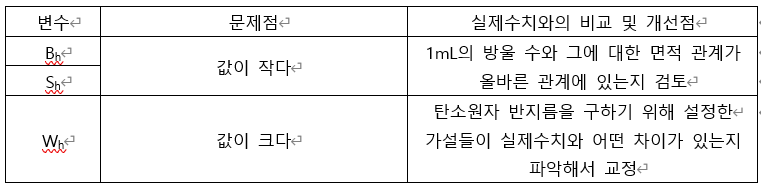
변수 Bh와 Sh는 서로 유사한 관계에 있으므로 둘을 묶어서 오류가 난 이유를 파악해보고, Wh는 가설과 실제수치의 비교를 통해 오류를 살펴보자.

1. Bh와 Sh의 오류가 실제 실험에 미친 영향

우선, 변수 Bh에 대한 오류는 크게 실험에 영향을 미치지 않았다고 생각한다. 비록 피펫의 한 방울의 크기가 다른 조와 평균적 수치보다 컸지만, 3번의 측정에도 1mL의 방울 수는 69~70개였기 때문이다. 그렇다면, 발생했던 문제는 구한 Bh에 대해 Sh의 값이 비교적 작게 나왔기 때문이라고 추론할 수 있다. 즉, 단분자층의 면적 형성과정에서 문제가 있었다고 생각할 수 있다. Bh의 수치가 작았다는 것은 hexane 한 방울 당 크기가 비교적 큼을 의미한다. 하지만 송화가루 도포의 문제, 헥세인 방울의 양이 1mL방울 수를 측정할 때와 다름의 문제, 같은 실험의 반복을 통한 잔여 스테아르 산 용액의 영향 등 여러 요인 때문에 구한 Bh에 대해 올바른 Sh값이 도출되지 않음을 예측할 수 있다.

2. Wh의 오류가 실제 실험에 미친 영향

Bh와 Sh의 오류도 비교적 중요한 오류이지만, Wh에 의한 오류의 영향이 더 크다. 원자 반지름 측정에는 여러 종류가 있지만 대표적으로는 공유결합선 반지름 측정과 반데르발스 반지름이 있다. 공유결합이 가능한 물질에 대해서는 공유결합선 반지름 측정을 통해 원자 반지름을 정의한다. 하지만 가정 3에서처럼 결합길이를 무시하고 모든 원자가 붙어있는 형태로 측정한다면, 실제 원자반지름 수치보다 더 큰 반지름 값을 얻는다. 즉, 실제 탄소 원자 반지름을 rfc라고 했을 때 다음과 같이 표현할 수 있다.

실제로는 탄소 원자가 단일결합으로 중첩된 형태를 띠고 있다. 그렇기에 실제 원자반지름과 가정에 의한 원자 반지름보다는 크기가 작으며 실수배 관계가 성립한다. 이를 식으로 표현하면 다음과 같다. 

$r_{fc}=kr_{c}=\frac{k\times l_{s}}{36\times\sin54.75^{\circ}}$ (단, 0<k<1)

이 과정을 통해 수정된 Wh를 W’h라고 한다면 Wh>W’h가 성립하므로 오차를 개선할 수 있다.

1번과 2번 오류가 이번 아보가드로 측정에서 오차를 내는데 크게 기인하지만, 수치의 측정을 눈으로 했다는 점도 실제 아보가드로 수와 결과가 다르게 나타나는 데 큰 원인이 된다. 그리고 계산과정 사이에서도 유효숫자가 제한된다는 점은 아보가드로 수를 구하는데 큰 영향력을 미친다. 또한, 실험과정에서 헥세인의 휘발성으로 인해 이러한 오류는 실험을 반복적으로 진행하던가, 보다 정밀한 도구를 사용한다면 다음에 같은 실험을 할 때 오차를 줄일 수 있을 것이라고 예상된다.

 

Ⅷ. Reference

1. Zumdahl, Chemistry 9th edition, CENGAGE Learning, 사이플러스, 2014, pp. 105~106, 531, 534~537

2. Brown 외 6인, Chemistry The Central Science 14th edition, Pearson, 2019, pp. 96

3. 대한화학회, 표준 일반화학실험 제 7판, 천문각, 2011, pp. 49~54