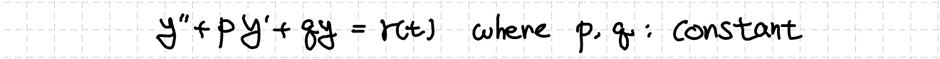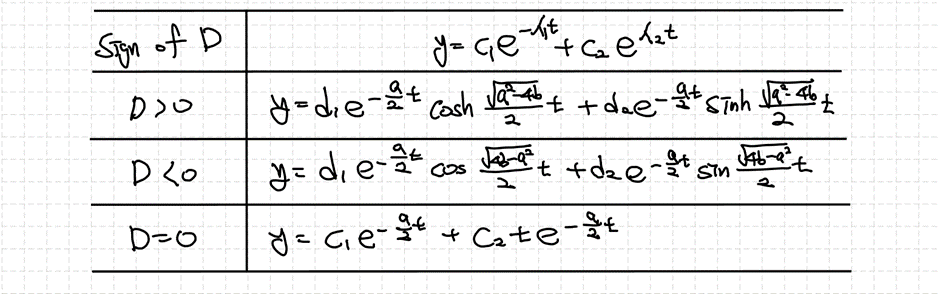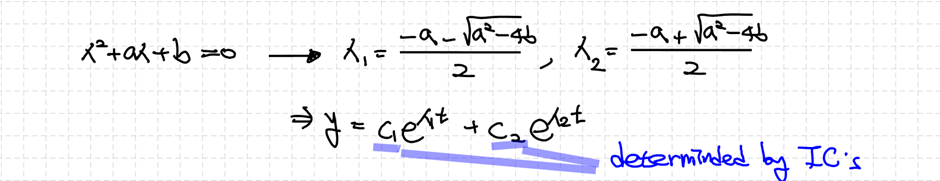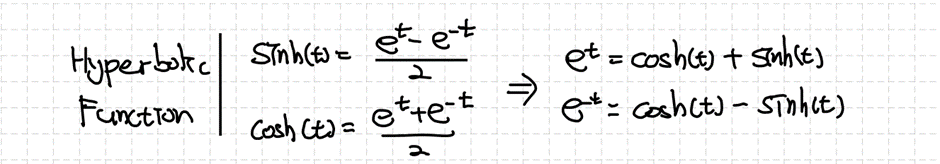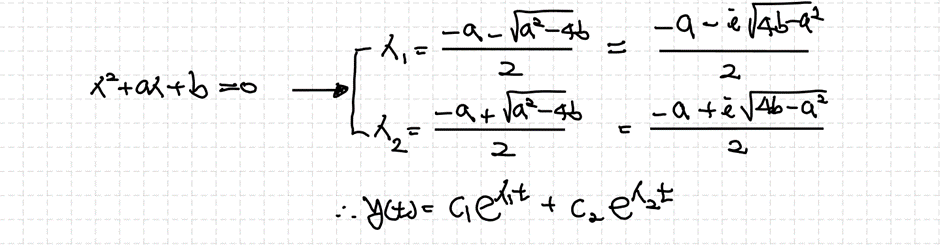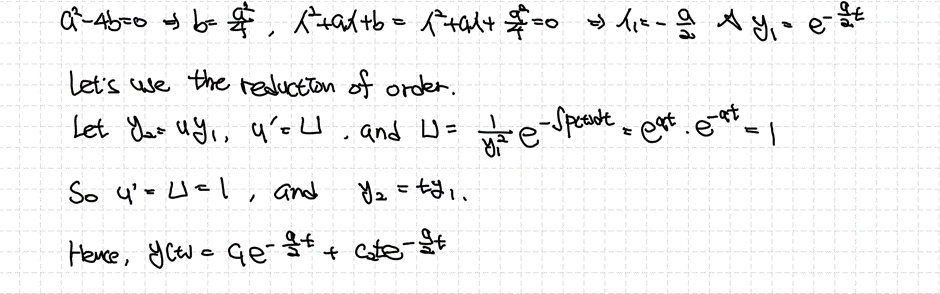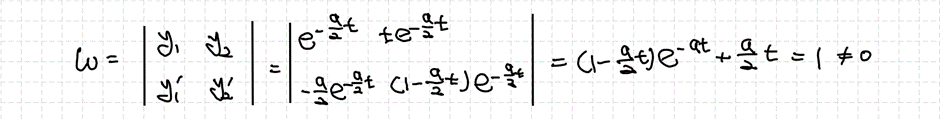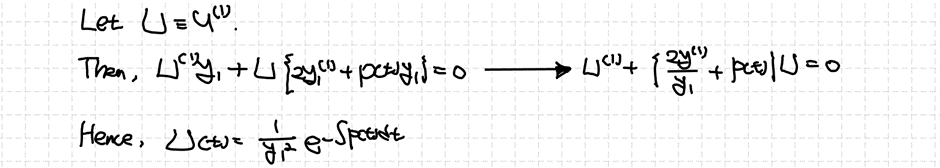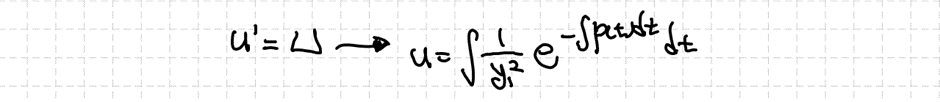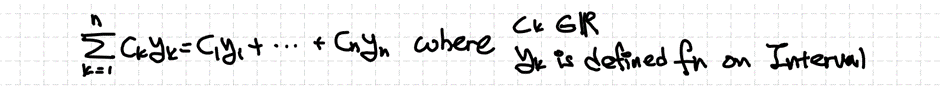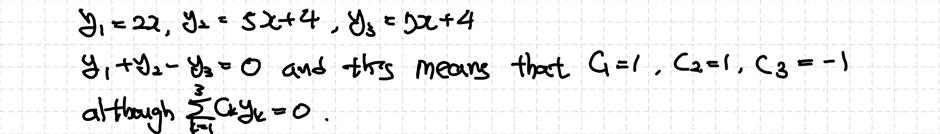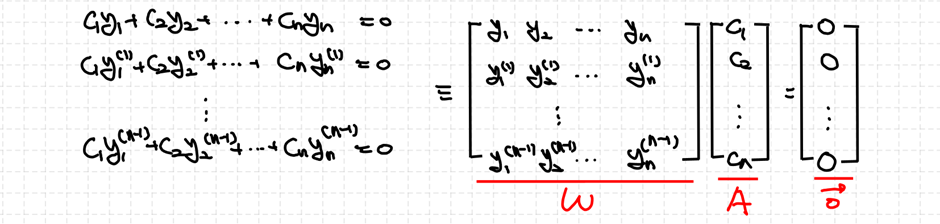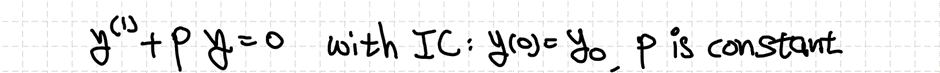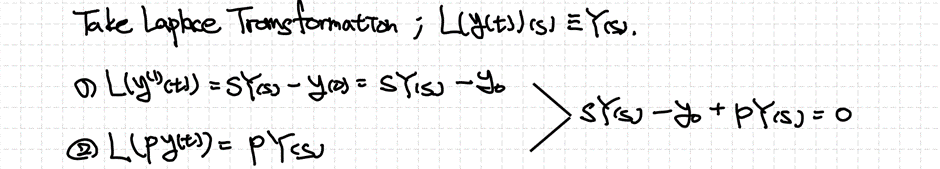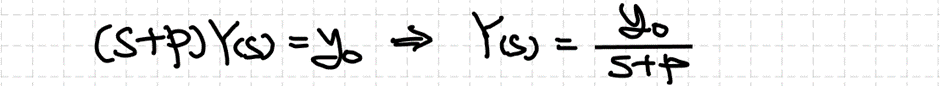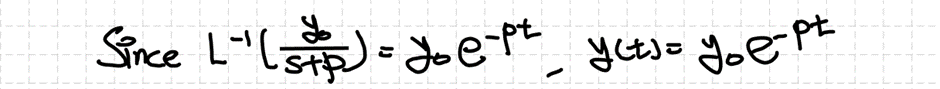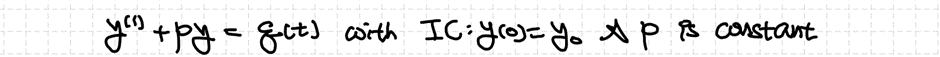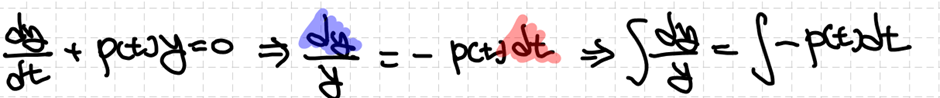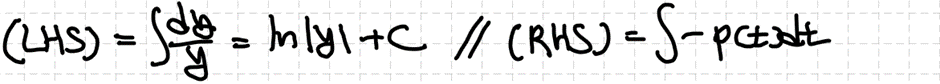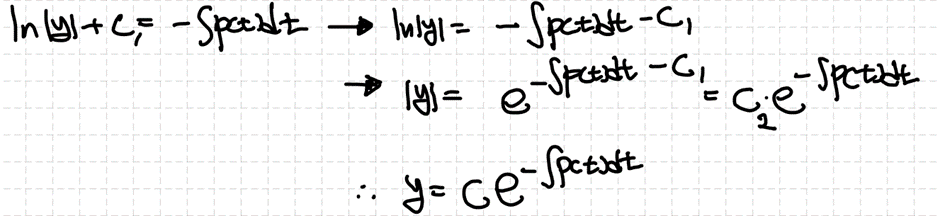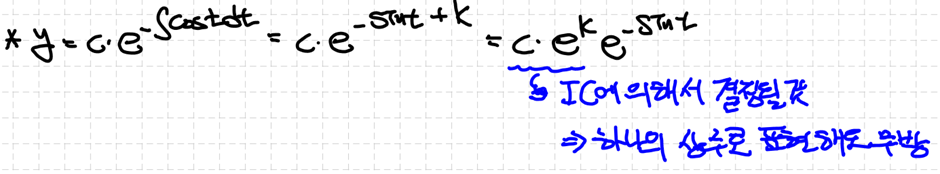화공노트: 화학공학 살펴보기

Contents

오일러-코시 방정식(Euler-Cauchy Equation)

지금까지는 상수만을 계수로 갖는 2차 상미분방정식들에 대해서만 살펴봤습니다. 하지만 많은 상미분방정식들은 계수들을 변수로 갖는 경우가 많습니다. 이때 우리는 급수해(Series Solution)을 이용해서 미분방정식의 해를 표현합니다. 이번에는 변수계수를 갖는 미분방정식의 예시인 오일러-코시 방정식(Euler-Calucy Equation)에 대해 살펴보고자 합니다.

오일러-코시 방정식(Euler-Cauchy Equation)

1) 형태

오일러-코시 방정식의 형태는 아래와 같고, 2차 ODE에 대해서도 정리할 수 있습니다.

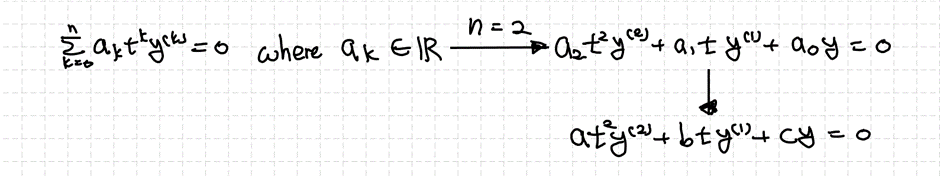
편의를 위해서 계수들을 각각 $a, b, c$로 표현한 것입니다.

2) 풀이

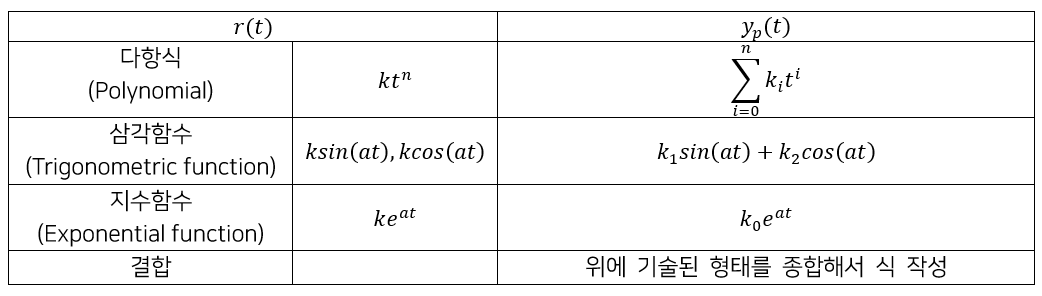
오일러-코시 방정식 풀이는 제차 2차 ODE를 풀이하는 것과 그 방식이 유사합니다. 우선 모든 단계를 전체적으로 살펴보겠습니다.

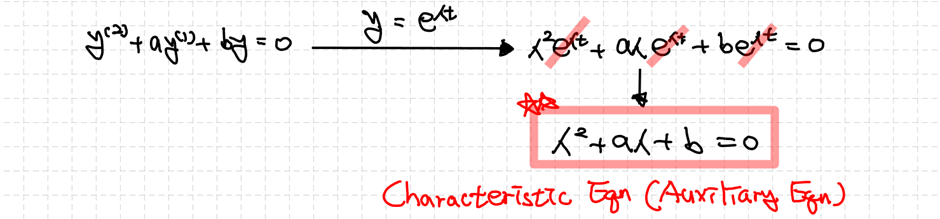
Step 1 trivial solution을 둔다. ($y(t)=t^m$)

Step 2 설정한 해를 방정식에 다시 대입해서 특성방정식을 얻는다. ($am ^2+(b-1)m+c)$)

Step 3 특성방정식에 따라 해의 형태를 결정한다.

상수계수를 갖는 제차 2차 ODE에서는 $y(t)=e^{λt}$로 설정한 것에서 $y(t)=t^m$으로 바꾸어 설정한 것이 변했고, 그래서 특성방정식도 다른 형태로 얻어진 것입니다. 그러면 특성방정식의 판별식의 부호에 따라 작성되는 식의 형태도 차이가 있음을 예상할 수 있을 것입니다. 조금 더 구체적으로 살펴보겠습니다.

설정한 식을 오일러-코시 방정식에 넣으면 식을 정리할 수 있습니다. 주어진 식이 만족하려면 $t^m=0$이거나 $m$에 대한 방정식이 0이여야 합니다. 하지만 $t^m=0$일 때 오일러-코시 방정식이 성립하는 것은 자명합니다. 그렇기에 해에서 어떠한 의미도 가져올 수 없습니다. 따라서 우리에게 의미가 있는 해를 얻기 위해서 필요한 조건은 $m$에 대한 방정식이 0인 것이고, 이를 특성방정식으로 생각할 수 있습니다. 좀 더 편한 계산을 위해 이 방정식을 $m$에 대해 정리할 수 있고 그 결과는 다음과 같습니다.

특성방정식이 $m$에 대한 2차방정식이므로 이를 계산해서 풀이할 수 있습니다. 하지만 특성방정식에서의 판별식 $D=(b-a)^2-4ac$의 부호에 따라 $m$의 형태가 달라질 것입니다. 각각의 경우 해가 어떻게 다르게 나타나는지 살펴보겠습니다.

3) $D$의 부호에 따른 해의 형태

(1) $D>0$: Real, two different roots

판별식의 부호가 양수라면 서로 다른 2개의 실근 $m_1, m_2$가 나올 것입니다.

(2) $D<0$: Complex, two different roots

판별식의 부호가 음수라면 복소수 형태를 갖는 서로 다른 2개의 실근이 얻어질 것입니다.

보다 편한 논의를 위해서 근의 실수부분을 $α$, 근의 복소수부분을 $β$라고 정의한 것입니다. 이를 이용해서 해를 표현하겠습니다.

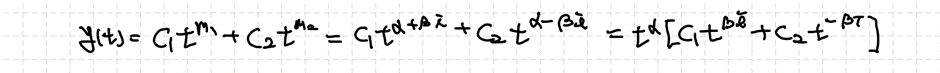
비교적 해의 형태가 간단하게 바뀌었지만, 여전히 지수에 허수 $i$가 있어서 계산 시에 불편할 수 있습니다. 이 문제는 Euler Identity를 이용해서 식의 형태를 편하게 바꿀 때 해결할 수 있습니다. 밑을 자연상수로 갖지 않는 형태이더라도 약간의 식의 변형을 통해 Euler Identity를 사용할 수 있습니다.

이를 이용해서 해를 정리할 수 있습니다.

(3) $D=0$ Double Root

판별식이 0일 때에는 하나의 해만 얻을 수 있기 때문에 차수축소법(Reduction of Order)을 이용해서 또 다른 기저해를 찾을 필요가 있습니다. 차수축소법을 모르거나 기억이 나지 않으면 아래의 링크를 참고하면 될 것 같습니다.

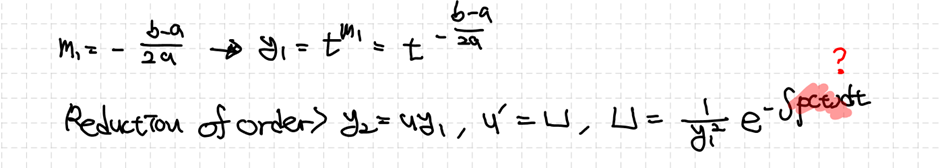
이때 $p(t)$가 어떠한 미분방정식에서 오는지 확인할 필요가 있습니다.

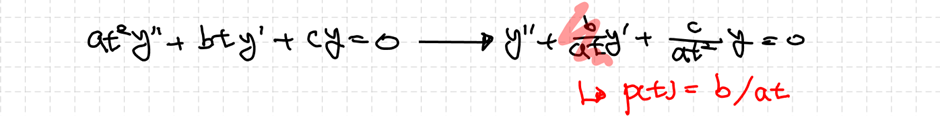
라그랑쥐 차수축소법 이용 시 적용하는 $p(t)$는 미분방정식의 최고차항 계수가 1일 때를 이야기한 것이므로 $b/(at)$인 것을 확인할 수 있습니다. 마저 $y_2$를 찾고 해를 결정하겠습니다.

아마 첫번째 줄에서 절댓값을 날리는 과정이 이해가 안될 수 있는데, 이는 끌고가서 계산을 하더라도 결국 $c_2$에 포함될 것을 감안하여 미리 계산의 편의를 위해 부호를 무시한 것입니다.

Contents

매개변수 변환법 (the method of Variation of Parameter)

 미정계수법은 상수계수를 갖는 2차 ODE를 풀이하기에 좋은 방법이지만, 시간이 비교적 오래 걸리는 단점이 있습니다. 그리고 $y_p(t)$의 형태가 $y_h(t)$에 포함되어 있는지도 해를 구하기 전에 미리 예측해야 하는 번거로움이 있습니다. 이러한 문제점들을 보완하기 위해 매개변수 변환법(method of Variation of Parameter)을 이용할 수 있습니다.

매개변수 변환법 (the method of Variation of Parameter)

1) 매개변수 변환법 개념

다음과 같은 미분방정식이 주어졌다고 생각하겠습니다.

이때 매개변수 변환법을 이용해서 $y_p(t)$를 구하는 것은 해의 형태를 아래처럼 둔다는 것을 뜻합니다

즉, 주어진 미분방정식이 제차 ODE일 때 얻은 해의 기저들의 계수를 하나의 변수로 두고, 이를 풀이해서 $y_p(t)$를 얻는 것입니다. 각각의 매개변수 계수 $u(t)$와 $v(t)$는 다음과 같습니다.

예시를 통해 이해해보도록 하겠습니다.

우선 제차 상미분방정식일 때의 해 $y_h(t)$일 때의 해부터 구하겠습니다.

그리고 매개변수 변환법을 이용해서 $y_p(t)$를 구할 수 있습니다.

그리고 주어진 초기조건을 이용해서 조건에 적합하는 유일한 해를 구할 수 있습니다.

2) 의의와 한계

매개변수 변환법을 이용하면 상수계수를 갖는 모든 2차 상미분방정식을 풀이할 수 있습니다. 또는 오일러 코시 상미분방정식 (Euler-Cauchy ODE, $t^2y’’+ty’+y=r(t)$)를 풀이할 수 있습니다. 하지만, 변수를 계수로 갖는 2차 상미분방정식을 풀이하는 데에는 제한이 있습니다. 이러한 미분방정식을 풀 때는 급수해(Series Solution)를 이용하거나 수치해석(Numerical Analysis)를 이용합니다.

Contents

미정계수법 (Method of Undetermined Coefficients)

미정계수법 (Method of Undetermined Coefficients)

미정계수법은 forcing function $r(t)$과 형태가 유사하게 특수해 $y_p (t)$를 설정해서 해를 구하는 것입니다. $y_p (t)$를 주어진 상미분방정식에 대입한 후 항등식의 결정방법 중에서 계수비교법을 이용해서 해를 결정합니다. forcing function의 형태에 따라 설정하게 되는 $y_p (t)$를 아래에 정리했습니다.

풀이과정은 다음과 같습니다.

Step 1 제차 방정식의 풀이

주어진 미분방정식에서 forcing function을 0으로 설정할 때 생기는 제차 미분방정식을 풀어줍니다. 혹시 그 방법을 모르겠다면 아래의 링크를 참고하면 되겠습니다.

6. 특성방정식과 상수 계수를 갖는 제차 2차 선형 상미분방정식의 풀이 :: 화공&책 리뷰 (tistory.com)

Step 2 특수해의 설정

위의 표를 참고해서 forcing function의 형태에 맞게 $y_p(t)$를 설정하고 대입한 후 계수비교를 통해서 형태를 결정합니다.

예시를 통해 설명해보겠습니다.

EX

주어진 문제가 다음과 같다고 하겠습니다. 우선 forcing function $e^t=0$으로 두면 제차 상미분방정식으로 형태가 변하고, 이는 특성방정식을 이용해서 풀이할 수 있습니다.

forcing function이 지수함수 형태를 띠고 있음을 이용해서 해를 결정할 수 있습니다. 그리고 주어진 초기조건을 이용해서 유일한 해 하나를 찾을 수 있습니다.

 ** 주의사항 **

만약 $y_p(t)$에 $y_h(t)$ 형태 중 일부를 포함하고 있다면 새롭게 $y_p(t)$를 설정해야 합니다. 이는 $t^k y_p(t)$로 설정하는 것을 의미합니다. 이때 $k$는 제차 ODE의 해의 형태와 겹치는 것이 없을 때 까지 그 크기를 높여주어야 합니다. 예를 들어보겠습니다.

위의 예시에서 $r(t)$만 $e^{3t}$로 바꾼 문제입니다. 하지만 이 forcing function은 $y_h(t)$에서 이미 등장하는 형태입니다. 그렇기에 아무리 $y_p(t)$를 결정하더라도 결국 $y_h(t)$에 흡수되어 제차 상미분방정식에 대한 해 밖에 얻지 못합니다. 따라서 $y_p(t)=Ate^{3t}$로 두고 식을 풀어야 합니다.

Contents

1. 상수계수를 갖는 2차 제차 선형 상미분방정식의 형태 (Homogeneous 2nd order linear ODE with Constant Coefficient)

2. 특성방정식(Characteristic Equation)과 상수계수를 갖는 2차 제차 선형 상미분방정식의 풀이 (Characteristic Equation and Solving Homogeneous 2nd order linear ODE with Constant Coefficient)

3. 특성방정식에 따른 해의 형태 구분 (Classification of Solution)

2차 ODE를 풀이하기 위해서는 우선 제차 2차 ODE를 풀이할 수 있어야 합니다. 우선 상수 계수를 갖는 제차 2차 선형 ODE를 어떻게 풀이하는 지를 알아보고자 합니다. 그 과정에서 정의되는 특성방정식(characteristic equation)의 형태에 대해서도 살펴보겠습니다. 이는 상미분방정식을 풀이하는 데에도 기본적으로 할 수 있어야 하는 계산이고, 심지어 편미분방정식을 풀이하는 데에도 사용됩니다. 그렇기에 처음 공부할 때 잘 기본을 다져야 할 필요가 있습니다.

1. 상수계수를 갖는 2차 제차 선형 상미분방정식의 형태 (Homogeneous 2nd order linear ODE with Constant Coefficient)

1) 정의에 따른 표현

상수계수를 갖는 2차 제차 선형 상미분방정식은 선형 상미분방정식의 정의로부터 표현될 수 있습니다.

이 상미분방정식이 2차라고 주어졌기 때문에 $a_2≠0$이고, 이를 이용해서 식을 정리한 것입니다.

2) 미분연산자(Differential Operator, $D$)를 이용한 표현

미분연산자는 미분기호를 보다 편하게 작성하기 위해 정의되었습니다. 미분연산자의 형태와 이를 이용해서 미분방정식을 표현할 수 있습니다.

미분연산자를 이용하면 마치 대수식처럼 미분방정식을 표현할 수 있습니다. 미분연산자의 차수를 보고 주어진 상미분방정식의 차수도 쉽게 파악할 수 있습니다.

** 여담이지만, 연산자(Operator)는 특정 물성값(observation)을 관찰하기 위해 취하는 도구입니다. 여기서 어떤 변수 $y$에 미분연산자의 조합 $D^2+aD+b$를 취하는 것은 해당 변수의 2차 상미분방정식을 얻어내겠다는 것과 같은 의미입니다.

2. 특성방정식(Characteristic Equation)과 상수계수를 갖는 2차 제차 선형 상미분방정식의 풀이 (Characteristic Equation and Solving Homogeneous 2nd order linear ODE with Constant Coefficient)

이제 어떻게 제차 2차 ODE를 풀이하는지 살펴보겠습니다. 우선 전반적인 풀이 순서를 먼저 보여주고, 각 단계에 대한 부가적인 설명을 하겠습니다.

Step 1 $y=e^{λt}$를 해로 설정합니다.

이렇게 해를 두는 이유를 논의하는 것은 꽤 어려운 일입니다. 이해를 돕기 위해 조금만 설명만 드리겠습니다. 보통 자연상수를 밑으로 하는 지수함수는 미분해도 형태를 거의 유지하고, 형태에 따라 계수에만 변화가 있을 뿐입니다. 그래서 $y=e^{λt}$를 해로 두면 추후 계산을 더 편리하게 진행할 수 있습니다.

Step 2 $y=e^{λt}$를 주어진 미분방정식에 대입한 후 식을 정리해서 대수방정식을 얻어냅니다.

우리가 $y=e^{λt}$를 해로 두었기 때문에 주어진 미분방정식에 대입해도 무방합니다. 지수형태가 그대로 남지만, 모든 항에 지수항이 있고, 이는 항상 양수이기에 나누어 소거할 수 있습니다. 마저 정리하면 대수방정식(Algebric Equation, AE)를 얻을 수 있습니다.

정리 결과 얻은 식 $λ^2+aλ+b$을 특성방정식(characteristic eqn)또는 보조방정식(auxiliary eqn)이라고 합니다. 이는 λ에 대한 2차 방정식이고, 판별식의 결과에 따라 해의 형태가 상이합니다. 조금 뒤에 자세하게 다루겠습니다.

Step 3 선형조합을 이용해서 일반해를 표현합니다.

특성방정식을 푼 후 $λ$를 구하면 주어진 ODE의 일반해를 표현할 수 있습니다.

여기서 $c_1$과 $c_2$는 초기조건 또는 경계조건에 의해 결정됩니다. 1차 ODE에서 초기조건에 1개가 필요했음을 생각하면, 2차 ODE에서는 2개의 초기조건 또는 2개의 경계조건이 있어야 모든 계수가 결정될 수 있음을 알 수 있습니다. 아래의 글을 읽어보면 미분방정식과 조건설정에 대해 좀 더 이해할 수 있을 것입니다.

부록 1 미분방정식과 조건설정 :: 화공&책 리뷰 (tistory.com)

3. 특성방정식에 따른 해의 형태 구분 (Classification of Solution)

위에서 구했던 특성방정식을 근의 공식을 이용해서 풀 수 있고, 그 결과는 다음과 같습니다.

결국 해의 형태는 모두 일반해처럼 표현됩니다. 하지만 판별식의 부호에 따라 편하게 사용할 수 있는 해의 형태에는 차이가 있습니다. 먼저 그 결과들을 요약해보고, 각각의 경우를 살펴보겠습니다.

1) $D>0$ : Real, two different roots

우선 판별식이 2개의 서로 다른 실근을 가지는 경우 나타나는 해의 방식에 대해 살펴보도록 하겠습니다.

일반해에서 각 기저해들의 계수들은 초기조건에 의해 정해집니다. 단순히 지수의 형태를 이용해서 해를 표현해도 무방하지만, 후에 편미분방정식을 풀이할 때에는 지수형태 보다는 다른 형태를 이용할 때 계산이 편한 경우가 많습니다. 이 경우에는 쌍곡선함수(Hyperbolic Function)이용해서 위의 일반해를 표현할 수 있습니다.

이를 일반해에 대입을 해서 식을 정리할 수 있습니다.

2) $D<0$ : Complex, two different roots

$D>0$일 때와 비슷하게 계산을 할 수 있습니다.

이 경우에는 Euler’s Identity에 의해 알려진 지수함수와 삼각함수의 관계를 이용해서 식을 다시 작성할 수 있습니다.

이를 일반해에 대입해서 다른 형태로 작성할 수 있습니다.

3) $D=0$ : Real, Double Root

중근을 갖는 경우에는 일차독립은 2개의 근을 한번에 찾아낼 수 없습니다. 그렇기에 일전에 배운 차수축소법을 이용할 수 있어야 합니다.

이때 새로 구한 $y_2$가 실제로 $y_1$에 대해 일차독립인지는 론스키안을 이용해서 확인해볼 수 있습니다.

계산결과 론스키안이 1로 반드시 0이 아니기 때문에 $y_2$는 $y_1$에 대해 일차독립인 것을 다시 확인할 수 있습니다.

Contents

1. 차수축소법 (the Reduction of Order)

2차 상미분방정식의 해를 표현하기 위해서 2개의 일차독립인 해의 기저가 필요합니다. 하지만 몇몇 경우 풀이의 결과로 단 하나의 해의 기저만 확인되는 경우가 있습니다. 예를 들어 $y_1=y_2$일 때도 일반해를 표현할 수 없게 됩니다. 따라서 $y_1$에 대해 독립이고 미분방정식에 해의 기저로 작동할 수 있는 또 하나의 해를 찾을 필요가 있습니다. 라그랑쥐의 차수축소법(the Reduction of Order)을 이용하면 또다른 해 $y_2$를 얻을 수 있습니다.

1. 차수축소법 (the Reduction of Order)

$y_1$을 제차 2차 선형 ODE를 풀이한 결과 얻은 하나의 해라고 생각해봅시다. 차수축소법을 이용하면 $y_1$과 독립이고 주어진 2차 ODE를 충족하는 또 다른 해 $y_2$를 얻을 수 있습니다.

이 식을 무조건 외우라고만 하면 어려움을 느낄 수 있습니다. 그렇기에 유도과정을 간략하게 살펴보겠습니다.

우선 $y_2$를 위의 형태를 따를 것이라고 생각하고, ODE에 넣어서 식을 정리할 수 있습니다.

이때 정리된 식에서 우리가 풀어야 하는 것은 $u$입니다. $y_1$은 이미 계산된 해이기 때문입니다. 하지만 우리는 아직 1차 ODE만 풀 수 있기에 $u’$을 치환해서 식을 계속 풀어나갈 수 있습니다.

$U$에 대한 1차 미분방정식을 풀이하면 $t$에 대해 정리된 식을 얻을 수 있습니다. 하지만 우리는 $u$를 구해야 하는 것이므로 치환된 형태를 다시 환원해야 합니다.

이 결과를 이용하면 우리는 $y_2$를 얻을 수 있을 것입니다. 사실 문제를 풀이할 때 이처럼 유도를 하나하나 하면 시간이 오래 걸립니다. 그렇기에 요약된 알고리즘을 살펴보겠습니다.

검은색 화살표 순서대로 정의를 한 후, 다시 역순으로 풀이를 해주기만 하면 $y_2$를 얻을 수 있습니다.

예시를 통해 이해해보겠습니다.

해당 2차 ODE를 풀면 $y_1$만 얻게 됩니다. 그렇기에 차수축소법을 이용해서 $y_2$를 구한 것입니다. 새로 구한 해가 미분방정식의 해가 될 수 있는지 알고 싶으면 이를 다시 대입하면 됩니다. 그 과정은 다음과 같습니다.

간단한 2차 ODE를 풀어보며 해의 존재성과 유일성을 이해해보고, 미분방정식에서의 조건설정을 살펴보겠습니다.

고등학교 시절 미적분을 공부할 때, 주로 수직선상에 위치한 물체의 운동을 다룹니다. 이를 위해 $x(t)$를 위치함수를 두고 속도함수 $x’(t)$, 그리고 가속도함수 $x’’(t)$에 대해 생각해본 적이 있을 것입니다. 해당 물체가 수직선상에서 가속도를 갖지 않는 등속도 운동을 한다고 생각해보겠습니다. 그러면 가장 단순한 2차 ODE를 세울 수 있으며, 이를 풀이할 수 있습니다.

해가 존재한다는 것은 위처럼 적분을 해서 미분방정식을 풀어 해를 구할 수 있음을 의미합니다. 하지만 이 해는 아직 유일하지 않습니다. $C_1$과 $C_2$의 적분상수가 존재하기 때문입니다. 2개의 미지수를 정하기 위해서 2개의 조건이 필요합니다.

(1) 초기조건(IC)을 이용한 유일한 해 결정

초기조건이 다음과 같이 제시되어 있다고 생각했을 때 적분상수들을 쉽게 결정할 수 있습니다.

이는 우리가 배웠던 등속도 운동을 하는 물체의 수직선상에서의 위치인 것을 알 수 있습니다.

(2) 경계조건(BC)를 이용한 유일한 해 결정

미지수의 개수만큼 조건이 있어야 미지의 정보를 결정할 수 있다는 것은 잘 알려져 있습니다. 이는 조건이 초기조건의 형태를 갖지 않더라도 해가 유일하게 결정될 수 있음을 뜻합니다. 경계조건(BC)를 이용해서도 해의 유일함을 결정할 수 있습니다. 초기조건에 시간에 중점을 두는 반면 경계조건은 대상의 위치를 표현하는 조건들입니다. 경계조건이 아래와 같을 때 마찬가지로 적분상수를 쉽게 결정할 수 있고, 유일한 해를 결정할 수 있습니다.

경계조건을 이용한 유일한 해의 결정은 보통 편미분방정식(PDE)에서 주로 사용됩니다. 추후 PDE를 다룰 때 경계조건에 대해 조금 더 이야기해보도록 하겠습니다.

조건의 종류가 해의 유일성을 결정하는데 중요한 것이 아닙니다. 조건의 ‘개수’가 중요한 것입니다. 미분방정식이 풀어지는 조건의 형태는 제한적이지만, 단순히 상미분방정식이 꼭 초기조건만으로만 유일한 해가 결정되는 것이 아님을 강조하고 싶었습니다. 대개 n차 상미분방정식의 경우 풀이하는 과정에서 n개의 적분상수가 생길 것임을 생각할 수 있기에 n개의 조건을 부여해야 유일한 해가 결정됩니다.

조금 더 구체적으로 생각해보면 $C_1$은 1번 미분된 해에서 나타나는 적분상수이고, $C_2$는 0번 미분된 해에서 나타나는 적분상수 이기 때문에 $C_1$에 대한 조건만 제시되지 않는 한 유일한 해를 결정할 수 있을 것입니다.

(3) 조건 조합을 이용한 유일한 해 결정

그렇다면 초기조건과 경계조건의 선형조합에 의해 제시된 조건도 미분방정식의 해를 유일하게 결정할 수 있는지에 대해 살려보겠습니다.

마찬가지로 유일한 해를 결정할 수 있습니다.

물체의 거동을 설명하는 미분방정식은 동일하더라도, 조건을 어떻게 부여함에 따라 나타나는 해의 형태는 다양합니다. 그래서 미분방정식에서 조건의 설정은 매력적인 행위입니다. 문제풀이를 할 때에는 조건에 대해 많이 고민하는 경우는 없을 것입니다만, 조건은 위의 이유 때문에 제시되었음을 생각해볼 수 있다고 기대합니다.

Contents

1. 2차 선형 상미분방정식의 형태 (the Formulation of 2nd order Linear ODE)

2. 2차 선형 미분방정식의 해의 존재성(Existence)과 유일성(Uniqueness)

3. 2차 상미분방정식의 해의 형태

4. 선형조합과 선형독립 (Linear Combination and Linear Independence)

2차 상미분방정식은 매우 중요합니다. 고전역학에서 속도-가속도 관계를 동시에 표현할 때 2차 선형 상미분방정식 형태를 얻을 수 있습니다. 그리고 많은 편미분방정식을 풀이하기 위해서 2차 상미분방정식을 풀 수 있어야 합니다. 그래서 2차 상미분방정식에 대해서는 조금 자세하게 다룰 필요가 있습니다. 그 중에서도 2차 선형 상미분방정식에 대한 개념을 전반적으로 살펴보도록 하겠습니다.

1. 2차 선형 상미분방정식의 형태 (the Formulation of 2nd order Linear ODE)

2차 선형 상미분방정식의 형태를 상미분방정식의 일반형태로부터 이끌어낼 수 있습니다.

1차 ODE처럼 2차 ODE도 forcing function $r(t)$의 유무에 따라 제차인지 비제차인지 구분됩니다.

2. 2차 선형 미분방정식의 해의 존재성(Existence)과 유일성(Uniqueness)

주어진 미분방정식을 풀이하는 것은 중요합니다. 강의를 들을 때 나오거나 전공서적에 나와있는 문제들은 모두 답이 나오도록 잘 짜여 있습니다. 만약 모델링을 거쳐 미분방정식을 얻어냈을 때, 해당 미분방정식의 해가 존재하는지 그리고 그 해를 유일하게 결정할 수 있는지를 알 필요가 있습니다. 존재성과 유일성은 증명이 가능한 성질이나, 우선 어떤 조건에서 해가 존재하고 또 유일할 수 있는지에 대해 살펴보고자 합니다.

1) 해의 존재성 (Existence)

2차 ODE에서 계수로 취해진 함수 ($p(t), q(t), r(t)$)가 미분방정식이 정의된 구간 $I$에서 연속일 때 해가 존재한다고 생각할 수 있습니다.

2) 해의 유일성 (Uniqueness)

2차 ODE에서 초기조건 $IC$가 다음과 같이 제시되어 있다면 해당 미분방정식은 1개의 유일한 해 (적합해)를 갖습니다.

즉 초기 조건이 2개는 제시되어야 해가 유일하게 결정됩니다. 이는 미분을 하면 정보량이 줄어들고, 반대로 적분을 하면 정보량이 증가하기 때문입니다.

3. 2차 상미분방정식의 해의 형태

1) 제차 상미분방정식의 해의 형태

제차 2차 선형 상미분방정식의 경우 자명한 해를 두어 ODE의 해를 구할 수 있습니다. 자세한 방법은 추후에 살펴보도록 합시다. 그 결과 얻어낸 두 해는 서로 일차독립(linearly independent)이여야 하고, 제차 미분방정식에서의 해는 그 둘의 선형조합(linear combination)으로 결정합니다.

2) 비제차 상미분방정식의 해의 형태

비제차 2차 선형 상미분방정식도 해를 얻을 수 있습니다.

이때 $y_h$는 $r(t)=0$으로 두고 해를 구하는 것입니다. 그리고 $y_p$는 차수비교법, 역연산자법, 그리고 매개변수 변환법을 이용해서 구할 수 있습니다. 마찬가지로 추후에 살펴보도록 하겠습니다.

4. 선형조합과 선형독립 (Linear Combination and Linear Independence)

2차 상미분방정식부터는 해의 기저들을 구하고, 이를 더하는 방식으로 해를 결정합니다. 선형조합, 선형독립, 선형종속에 대해 알아야 합니다.

1) 선형조합 (Linear Combination, Superposition)

선형조합은 기저들을 더하는 것을 얻을 수 있고 수학적으로는 아래처럼 표현합니다.

2) 선형독립과 선형종속 (Linear Independence and Linear Dependence)

선형독립과 선형종속은 선형조합에서 사용된 기저해($y_k$)의 일차독립성을 판단하는 것입니다. 만약 선형조합이 0일 때 기저해의 계수들이 어떠한 형태로 나타나는 지에 따라 선형독립인지 아닌지 결정됩니다. 수학적으로는 다음과 같이 표현할 수 있습니다.

이해가 안 될 수 있으니 예시를 통해 설명해드리겠습니다.

어떠한 3개의 기저해가 있을 때 이를 적당히 더해서 0을 만들 수 있습니다. 즉, 선형조합이 0이 될 때 모든 계수 $c_k$가 0이 되지 않는 조합이 존재하므로 세 함수는 선형종속임을 알 수 있습니다.

선형독립성을 분석해야 하는 함수의 개수가 적으면 적당한 조합으로 그 독립성을 판단하기 쉽습니다. 하지만 해의 형태가 단순한 다항식이 아니거나, 분석해야 하는 함수들의 해수가 너무 많을 때에는 독립성을 판단할 때 실수하기 쉽습니다. 그래서 다른 수학적 도구를 이용해서 선형독립을 판단합니다.

3) 론스키안(Wronskian)

어떠한 구간 $I$에 대해 정의된 $(n-1)$번 미분가능한 해 ${y_1, y_2,⋯,y_n}$에 대해 다음과 같은 수학적 표기를 할 수 있습니다.

이때 우리가 정의한 행렬 $W$를 론스키안(Wronskian)이라고 합니다.

그리고 행렬 A에 따라서 선형독립과 선형종속이 결정됩니다.

즉, 주어진 해들이 선형종속일 때 론스키안의 Determinant가 0인 것을 결정할 수 있으며, 우리는 명제의 논리를 이용해서 다음의 결과를 얻을 수 있습니다.

즉, $det(W)$이 0이 아니라면 우리는 얻어낸 해를 바로 사용할 수 있음을 의미합니다.

Contents

1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이

2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이

미분방정식 풀이과정을 따르지 않더라도 1차 상미분방정식을 풀이할 수 있습니다. 라플라스 변환을 이용해서 대수식을 정리하고 다시 라플라스 역변환을 이용하면 미분방정식의 해를 구할 수 있습니다.

1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이

예시를 통해서 라플라스 변환을 이용해서 ODE를 풀어내는 방법을 살펴보겠습니다.

EX

우선 각 항에 라플라스 변환을 취해서 식을 대수 영역으로 전환해줍니다.

그 후 라플라스 변환이 취해진 해에 대해 식을 다시 정리할 수 있습니다.

우리가 원하던 해는 대수방정식의 해가 아니라 미분방정식의 해이기 때문에 위의 결과에 라플라스 역변환을 취해줍니다. 그러면 미분방정식의 해를 얻을 수 있습니다.

2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이

제차 미분방정식을 풀이할 때와 마찬가지로 라플라스 변환을 취하고, 라플라스 변환된 해에 대해 식을 정리할 수 있습니다.

정리된 식의 형태를 살펴보면 homogeneous 일 때의 해($Y_h(s)$)와 특수해($Y_p(s)$)의 조합인 것을 확인할 수 있습니다. 이제 라플라스 역변환을 취하면 미분방정식의 해를 구할 수 있을 것입니다.

이해를 위해 예시를 살펴보겠습니다.

EX

우선 라플라스 변환을 취해서 대수방정식을 얻은 후 식을 정리합니다.

이제 라플라스 역변환을 취해 식을 정리해주어야 하는데, 이를 위해서 식을 재정리할 필요가 있습니다. 보통 라플라스 역변환을 위한 식 정리는 유리식의 항등성을 이용합니다.

라플라스 역변환을 취하면 미분방정식의 해를 얻을 수 있습니다.

여기서 $H(t)$는 Heviside Step Function이고, 주어진 미분방정식을 $t>0$에 대해 고려하면 $H(t)=1$로 두고 미분방정식의 해를 사용하면 됩니다. (사실 $t$가 시간인 경우가 많아 $t>0$에 대해서 고려하긴 합니다.)

Contents

1. 1차 선형 상미분방정식의 형태 (Formula of the first order ODE)

2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)

   - 제차 1차 선형 상미분방정식의 풀이

   - 비제차 1차 선형 상미분방정식의 풀이

1. 1차 선형 상미분방정식의 형태 (Formula of first order ODE)

1차 선형 상미분방정식은 아래의 형태를 갖습니다.

종속변수가 총 미분된 횟수를 미분방정식에서의 차수라고 생각할 수 있습니다. 여기서는 y가 한번 미분되었다는 것을 나타내기 위해 ‘ 대신 (1)을 윗첨자로 사용했습니다. 마찬가지로 forcing function으로 사용된 q(t)가 0이면 이 미분방정식은 homogeneous ODE이며, 0이 아니라면 Inhomogeneous ODE입니다.

2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)

1) 제차 1차 선형 상미분방정식 (Homogeneous 1st order Linear ODE)

초기조건(IC)이 주어진 homogeneous ODE는 다음과 같습니다.

이 문제는 변수분리법(Separating Variables)을 이용해서 비교적 쉽게 해결할 수 있습니다.

변수분리법은 적분하고자 하는 변수들을 한 곳에 몰아 적분을 비교적 편하게 수행하도록 하는 기법입니다. 이 상황에서는 dy 와 dt를 각 항으로 분리해서 식을 다시 작성할 수 있습니다.

왼쪽 항은 적분이 가능하지만 오른쪽 항은 p(t)의 형태에 의존하기에 문제 상황에 맞게 계산해야 합니다.

적분상수는 결국 초기조건에 의해 결정됩니다. 그렇기에 위의 과정을 거쳐 식을 정리할 수 있습니다.

예시 상황을 들어 초기조건을 적용하는 방법을 보여드리고자 합니다.

EX

이때 * 과정을 이해하기 조금 어려울 수 있습니다. 표현만 같은 거지 엄밀하게 따지만 다른 상수이긴 하지만, 결국 초기조건에 의해서 정해지는 값이므로 표현해둔 것입니다. 초기조건을 대입해서 상황에 적합한 해를 얻을 수 있습니다.

2) 비제차 1차 선형 상미분방정식 (Inhomogeneous 1st order Linear ODE)

초기조건(IC)이 주어진 inhomogeneous ODE는 다음과 같습니다.

inhomogeneous ODE는 ODE의 일반형이라고 생각할 수 있습니다. 이 ODE의 해는 적분인자(Integrating Factor)를 이용해서 유도할 수 있습니다. 그 결과는 다음과 같습니다.

여기서 C는 문제 조건에 의해 정해질 것입니다.

다만 이 공식을 적용할 때 유의해야 하는 부분이 있습니다. 1차 미분된 항 앞의 계수가 1임을 반드시 확인해야 합니다. 예시를 통해서 살펴보겠습니다.

주어진 미분방정식의 1차항 계수가 3이기 때문에 이를 1로 만들어야 하고, 이를 위해 3으로 나누어서 다시 ODE를 작성한 것입니다. 이를 위의 식에 넣어서 계산할 수 있습니다.

초기조건을 이용해서 상수 C를 결정할 수 있습니다.

나타나는 해의 형태를 다시 정리했을 때 homogeneous ODE 였을 때의 해에 특수해가 더해진 것임을 다시 한번 확인할 수 있습니다.

Contents

1. 선형 상미분방정식 (Linear ODE)

2. 상미분방정식의 일반해 (General Solution of ODE)

3. 초기조건(Initial Condition, IC)과 경계조건(Boundary Condition, BC)

4. 미분방정식의 해 구하기 (Solving ODE)

미분방정식은 화학공학에서 빼놓을 수 없는 수학적 도구입니다. 아무리 식을 잘 세워놓았더라도 미분방적식을 풀이할 수 없다면 문제 상황에서의 해답을 찾을 수 없습니다. 개념설명과 문제풀이를 바탕으로 미분방정식에 대해 공부해고자 합니다.

1. 선형 상미분방정식 (Linear ODE)

미분방정식에 하나의 변수만 개입되어 있을 때, 우리는 이 미분방정식을 상미분방정식(Ordinary Differential Equation, ODE)라고 합니다. 그 중에서 선형 미분방정식은 다음과 같이 작성할 수 있습니다.

forcing function이 0일 때 우리는 이를 제차상미분방정식(Homogeneous ODE)라고 합니다. 만약 그렇지 않은 경우에는 이 미분방적식을 비제차상미분방정식(Inhomogeneous ODE)라고 합니다.

2. 상미분방정식의 일반해 (General Solution of ODE)

1) 제차상미분방정식의 일반해

제차상미분방정식은 미분방정식으로부터 얻어지는 해들의 선형조합으로 일반해를 얻을 수 있습니다.

2) 비제차상미분방정식의 일반해

비제차상미분방정식은 해당 미분방정식이 제차였을 때 얻어지는 해와 비제차일 때 얻을 수 있는 특수해의 선형조합으로 일반해를 표현합니다.

3. 초기조건(Initial Condition, IC)과 경계조건(Boundary Condition, BC)

우리가 얻는 미분방정식과 그 일반해는 대개 지배방정식(Governing Equation)인 경우가 많습니다. 즉 보편적으로 나타나는 현상들을 설명할 수 있는 수식임을 의미합니다. 하지만 공학에서는 이러한 문제들을 자신의 상황에 맞게 적용해서 결과를 얻어야 합니다. 그래야 해당 문제를 정량적으로 풀어낼 수 있습니다. 그래서 미분방정식의 적합해를 끌어내기 위해서 초기조건 또는 경계조건이 필요합니다. 구체적으로 문제풀이를 시작할 때 자세히 살펴보겠습니다.

4. 미분방정식의 해 구하기

상미분방정식은 2가지 관점에서 해를 구할 수 있습니다  

1) 미분방정식의 해를 직접 구하는 경우

대개 알려져 있는 미분방정식의 경우 문제를 푸는 순서가 정해져 있습니다. 즉 공식 등에 대입해서 문제를 바로 풀이할 수 있습니다.

2) 라플라스 변환을 이용해서 해를 구하는 경우

1)의 방법으로 문제를 풀이하면 적분 연산이 필수적인데, 이는 번거로움을 동반합니다. 그래서 라플라스 변환을 이용해서 미분된 형태의 식을 대수방정식(Algebric Equation, AE)로 변환해서 식을 정리한 후 다시 라플라스 역변환을 통해 해를 구할 수 있습니다.

우선 주어진 미분방정식에 라플라스 변환을 취해줍니다. 그 후 식을 정리해서 라플라스 변환이 취해준 해와 나머지 항들을 분리해서 적어줍니다.

 그 후 라플라스 역변환을 취해서 다시 원래 구해야 하는 해를 얻을 수 있습니다.