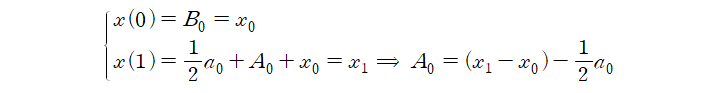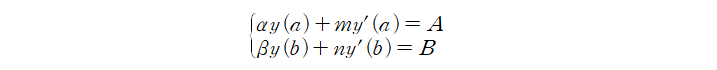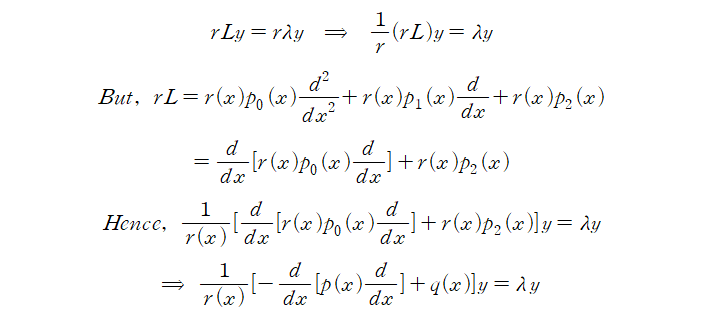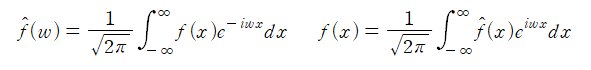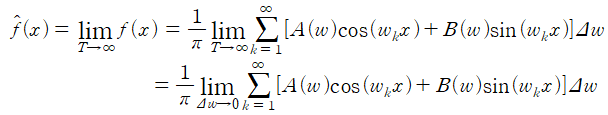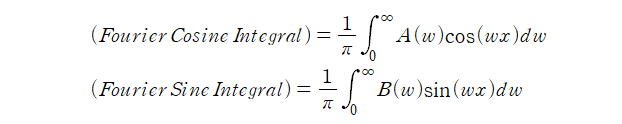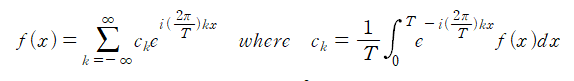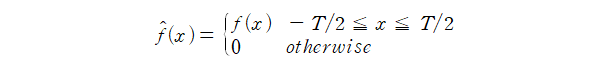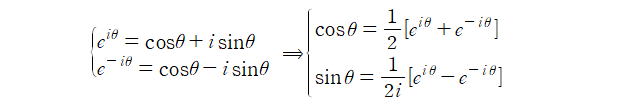화공노트: 화학공학 살펴보기

Contents Preview

안녕하세요 화공노트입니다. 지금까지 편미분방정식 풀이를 위해 필요한 개념 2가지(푸리에 급수, 스트룸 리우빌 문제)에 대해 살펴봤습니다. 드디어 편미분방정식 공부를 위한 준비를 마쳤습니다.

이번 글에서는 우리가 주로 다룰 편미분방정식의 형태와 종류, 그리고 이를 분류하는 방법에 대해 살펴볼 것입니다. 편미분방정식은 상미분방정식과 달리 조건 설정이 매우 유의미합니다. 그렇기에 편미분방정식에서의 조건 설정과 조건이 갖는 의미에 대해서도 살펴보겠습니다.

1. 편미분방정식의 형태 (Formation of Partial Differential Equation)

편미분방정식은 상미분방정식과 달리 서로 다른 2개 이상의 변수를 포함하고 있습니다. 대부분 시간-공간 변수들이 관여합니다. 이해를 돕기 위해 선형 2차 편미분방정식(linear second order partial differential equations)을 살펴보겠습니다.

1) 미분 횟수 고려

종속변수 $u$에 대해 앞의 세 항은 2번 미분되었고, 뒤의 세 항은 1번 미분됨을 알 수 있습니다.

2) 제차, 비제차

한편, 등호 오른쪽에 있는 항 $g$의 형태가 이 편미방의 제차, 비제차 여부를 결정합니다. 만약 $g$가 0이라면 이 방정식은 제차(homogeneous)이며, 0이 아니라면 비제차(inhomogeneous)임을 알 수 있습니다.

2. 편미분방정식의 분류와 예시 (Classification of PDE and Examples)

1) 편미분방정식의 분류

어떤 편미분방정식의 문제가 주어졌을 때, 이 방정식의 형태를 구분하는 것이 중요합니다. 2차 미분항(2nd Differential Terms)의 계수관계를 이용하면 주어진 방정식의 종류를 판단할 수 있습니다.

이 식은 이차방정식에서 판별식하고 매우 형태가 유사합니다. 이 식의 부호에 따라 방정식의 종류를 구분할 수 있습니다. 음수라면 타원형 편미분방정식(Elliptic PDE), 양수라면 쌍곡선형 편미분방정식(Hyperbolic PDE), 그리고 0이라면 포물선형 편미분방정식(Parabolic PDE)이라고 합니다.

2) 편미분방정식의 예시

각 종류의 편미분방정식에 대표적인 예시를 살펴보겠습니다

(1) 쌍곡선형 편미분방정식 ($b^2-4ac>0$)

양자역학에서 주로 등장하는 파동방정식(Wave Equation)은 쌍곡선형의 대표 예시라 할 수 있습니다.

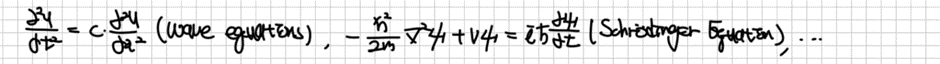
(2) 포물선형 편미분방정식 ($b^2-4ac=0$)

열 및 물질전달에서 분자 사이의 접촉으로 인해 물질, 열, 에너지 등이 전달되는 내용을 배울 수 있습니다. 이를 설명하는 열 전도 방정식(또는 확산 방정식, Heat/Diffusion Equation)은 포물선형의 대표적인 예시라 할 수 있습니다.

(3) 타원형 편미분방정식 ($b^2-4ac<0$)

한편, 라플라스 방정식(또는 포텐셜 방정식, Laplace/Potential Equation)은 타원형 편미분방식을 대표하는 예시입니다.

3. 편미분방정식의 풀이를 위한 조건 설정 (Setting Condition for Solving PDE)

1) 편미분방정식의 해의 특성

편미분방정식을 풀이하면 해의 다양성을 확인할 수 있습니다. 같은 방정식으로부터 시작하더라도 경계조건과 경계조건에 의해 최종 형태는 상이합니다.

많은 공학관련 전공을 공부할 때, 현상을 일반적으로 설명하는 방정식들을 유도할 때가 있습니다. 이 식에 문제 상황을 나타내는 조건을 설정하고 풀이할 때 해를 얻을 수 있습니다. 즉, 여러분은 정량적인 예측을 하기 위해 식을 유도하고 풀이하게 되는 것이지요.

2) 풀이를 위해 필요한 조건의 개수

편미분방정식을 풀이하기 위해 조건을 적절히 설정해주어야 합니다. 시간과 관련된, 그리고 공간과 관련된 변수에 대해 설정해야 하는 조건, 그리고 그 개수는 다음과 같습니다.

(1) 시간변수와 관련된 항은 초기조건(Initial Condition, IC)을 설정하고, 공간변수와 관련된 항은 경계조건(Boundary Condition)을 설정한다.

(2) 각 변수에 대해 미분 차수만큼 조건이 필요하다.

파동방정식을 예로 들어 조건 설정의 이해를 돕고자 합니다

시간과 관련된 항에 대해서는 초기 조건을, 공간과 관련된 항에는 경계 조건을 각각 2개씩 설정해야 함을 알 수 있습니다. 둘 다 미분이 2번씩 되어있기 때문입니다. 조건과 관련된 내용이 더 궁금하다면 아래의 글이 도움이 될 것입니다.

3) 경계조건의 물리적 의미

경계조건은 초기조건의 또 다른 형태입니다. 하지만 경계조건은 몇 가지 물리적 의미를 포함하고 있습니다.

(1) 경계조건은 어떤 시스템의 양 끝 정보만 표현하지만, 이를 이용해서 해를 결정하면 분석하고자 하는 시스템의 물성의 분포를 알 수 있도록 도와줍니다.

(2) 그렇기에 실험 분석 시 편미분방정식을 활용해야 할 때, 시스템 내부의 정보를 알기 위해서 올바른 경계조건만 설정해주면 됩니다.

Contents Review

지금까지 편미분방정식의 형태와 종류를 알아보고, 어떤 종류인지 분류하는 방법을 살펴봤습니다. 그리고 이를 풀이하기 위해 조건을 설정하는 방법에 대해서도 살펴봤습니다.

다음 글에서는 편미분방정식을 풀이할 때 가장 많이 사용하게 될 변수분리법(Separation of Variables)에 대해 살펴보겠습니다.

글에 관해 궁금한 점이 있으면 댓글 남겨주세요.

감사합니다.

Contents Preview

지금까지 스트룸 리우빌 이론이 무엇인지, 스트룸 리우빌 연산자가 어떤 특성을 갖고 있는지 살펴봤습니다. 이번 글에서는 스트룸 리우빌 이론의 가장 단순한 예제를 같이 살펴보며, 실제 상미분방정식을 풀이하는 데 스트룸 리우빌 이론이 어떻게 이용될 수 있는지 살펴보겠습니다.

스트룸 리우빌 이론을 이해하기 위해 간단한 예시를 살펴보겠습니다.

어떠한 이차 상미분 방정식은 스트룸 리우빌 연산자를 이용해서 작성될 수 있었습니다. 실제로 그런지 살펴보겠습니다.

스트룸 리우빌 연산자에서 $p, q, r$이 각각 $-1, 0, 1$이 될 때 예시로 가져온 미분연산자가 될 수 있음을 확인할 수 있습니다. 그렇기에 주어진 미분방정식을 고윳값 문제로 해석할 수 있습니다.

첫번째 등호 관계는 주어진 미분연산자를 취한 형태를 표현한 것이고, 두 번째 등호는 미분연산자에 대해 고윳값 문제를 나타낸 것입니다. 이제 문제를 풀기 위해 두 등호 사이의 관계를 얻을 수 있습니다. 그 결과 주어진 문제를 2차 선형 상미분방정식으로 해결할 수 있음을 알게 됩니다.

결국, 미분방정식을 풀이해서 고윳값(eigenvalue)을 얻을 수 있고, 이때 얻은 해는 고유함수(eigenfunction)라고 말할 수 있습니다.

2차 선형 상미분방정식은 특성방정식(characteristic equation)을 이용해서 풀이합니다. 이 문제의 경우 고윳값의 부호가 상미분방정식의 해의 형태를 결정합니다. 각 고윳값의 부호에 따라 상미분방정식의 해가 어떻게 나타나는지 살펴보겠습니다.

특성방정식의 풀이는 결국 이차방정식의 풀이로부터 시작됩니다. 그렇기에 고윳값의 부호에 따라 얻어지는 근의 개수 및 형태가 다르며, 이를 정리할 수 있습니다. 고윳값이 양수일 때는 포물선 함수(Hyperbolic Function)을, 고윳값이 음수일 때는 오일러 항등성(Euler’s Identity), 그리고 고윳값이 0인 중근을 가질 때에는 라그랑쥐의 차수 축소법(Reduction of Order)을 이용했습니다. 결과를 다시 요약하겠습니다.

한편, 조건을 만족하는 해를 얻기 위해 경계조건을 대입해봐야 합니다. 이를 위해 일반해에 경계조건을 대입해서 자명하지 않은 해(nontrivial solution)를 얻어야 합니다. 이때 자명하지 않은 해란 조건을 만족하는 해가 0이 아닌 어떠한 해를 의미합니다. 직접 대입해보며 살펴보겠습니다.

고윳값이 0 이상인 경우, 주어진 경계조건을 만족하기 위해서는 계수가 모두 0이 되어 해도 0이 됩니다. 이는 우리가 미분방정식을 풀지 않아도 얻을 수 있는 자명한 해입니다. 그렇기에 이 경우는 주어진 문제의 답이 될 수 없습니다. 정확히는 크게 의미 있는 정보를 주지 않습니다.

고윳값이 음수인 경우는 조금 다른 양상을 보입니다. 경계조건을 만족시키는 어떠한 고유함수가 존재할 수 있으며, 이는 고윳값의 결정으로 정해지게 될 것입니다.

고유함수의 직교성을 이용한다면, 경계조건을 만족하는 어떤 함수를 고유함수의 선형조합으로 표현할 수 있다는 사실을 배웠습니다. (Eigenfunction Expansion) 이를 나타내면 다음과 같습니다.

주어진 문제에 대한 고유함수를 선형조합으로 표현했더니 푸리에 사인 급수(Fourier Sine Series)임을 알게 되었기에, 각 고유함수에 대한 계수를 구하는 것은 어렵지 않을 것입니다.

Contents Preview

에르미트 연산자에 대한 고윳값 문제를 풀면, 서로 직교하는 고유함수들을 얻을 수 있습니다. 스트룸-리우빌 연산자도 동일한 특성을 갖고 있습니다. 이를 증명하고 직교성을 이용해서 어떤 구간 내의 함수를 고유함수의 선형조합으로 표현하는 방버에 대해 살펴보겠습니다.

고윳값 문제를 해결하면 고윳값과 이에 해당하는 고유함수를 구할 수 있습니다. 연산자의 종류에 따라 고유함수의 특성이 달라지는데, 에르미트 연산자에 대한 해는 서로 직교하는 특성이 있습니다. 앞서 스트룸-리우빌 연산자의 자기수반성 증명을 통해 이 연산자도 에르미트 연산자로 생각할 수 있으며, 그렇기에 스트룸-리우빌 연산자의 해도 서로 직교할 것이라고 예상할 수 있습니다. 이를 간단하게, 그리고 실제 내적을 통해 식을 조정해보면서 증명해보도록 하겠습니다.

<증명 1> 고윳값 문제를 이용한 고유함수의 직교성 증명

서로 다른 두 고윳값에 대해, 그리고 고유함수에 대해 생각해보겠습니다. 연산자의 자기수반성을 이용해서 식을 표현했습니다. 고윳값-고유함수 관계를 이용해서 식을 마저 전개해보겠습니다.

두 고윳값은 서로 다르기에 내적의 결과가 0이 되어야 합니다. 이는 결국 두 고유함수가 서로 직교함을 의미합니다.

위의 증명은 고윳값 문제 관계를 이용해서 고유함수의 직교성을 증명한 것입니다. 내적을 전개하고, 식을 변형해보면서 직교성을 다시 한 번 증명해보도록 하겠습니다.

<증명 2> 내적을 전개, 변형해서 보이는 고유함수의 직교성

어떤 두 함수가 직교한다면, 내적의 결과는 0일 것입니다. 우선 고윳값 $\lambda$에 대한 고유함수를 이용해서 식을 변형해보겠습니다.

의 식을 내적 형태로 바꾸기 위해 식을 변형하겠습니다.

처음 시작을 $\lambda$에 대한 고유함수로부터 내적을 표현했습니다. $\mu$에 대한 고유함수로부터도 식을 전개할 수 있으며, 이를 나타내면 다음과 같습니다.

두 내적 사이의 관계를 표현하기 위해서 (*)과 (**)의 차이를 구해보겠습니다.

스트룸-리우빌 연산자의 자기수반성을 증명할 때와 비슷한 결과를 얻을 수 있습니다. 어떤 특정 수치는 결국 경계 조건에 의해서 소거되고, 그래야 내적의 결과가 0인 것을 얻을 수 있습니다. 경계조건의 대입을 통한 항의 처리는 생략하고, 증명을 마무리해보겠습니다.

<증명 1>과 결국 내용이 비슷합니다. 서로 다른 고윳값의 차가 0이 될 수 없으니 반드기 고유함수 사이의 내적이 0이 되어야 하는 것을 알 수 있습니다. 이는 두 고유함수가 서로 직교한다는 것을 뜻합니다.

한편, 고유함수의 직교성을 이용하면 경계조건을 만족하는 함수를 고유함수의 선형조합으로 표현할 수 있습니다.

고유함수의 선형조합으로 경계조건을 만족하는 함수를 표현할 수 있고, 내적을 이용해서 고유함수의 계수를 결정할 수 있습니다. 이 특성을 증명해보겠습니다.

어떤 함수를 고유함수의 내적으로 표현했을 때, 내적을 통해서 특정 계수만을 남길 수 있습니다. 그렇기에 함수를 스트룸-리우빌 연산자에 대한 고유함수들의 조합으로 표현할 수 있습니다.

아마 공학수학 또는 수리물리학을 공부한 분들이라면 위의 식과 유사한 형태를 푸리에 급수에서 살펴볼 수 있었을 것입니다. 푸리에 급수도 가중치가 1인 내적을 이용한 고유함수의 조합을 이용한 것이기 때문입니다.

Contents Preview

스트룸-리우빌 연산자가 에르미트 연산자이기 때문에, 이 연산자의 성질을 공유할 것입니다. 그 중에서 에르미트 연산자의 고윳값 문제를 풀었을 때 얻은 고윳값은 항상 실수인 특성을 스트룸-리우빌 연산자에서도 동일하게 나타나는 것을 보일 것입니다.

스트룸-리우빌 연산자도 고윳값 문제로 생각할 수 있습니다. 이를 식으로 나타내면 아래와 같습니다. 

우리가 보이고자 하는 고윳값은 위의 관계에서 확인할 수 있습니다. 이 문제를 풀어서 얻은 고윳값이 실수라는 것을 뜻합니다, 이제 증명을 시작하겠습니다.

<증명>

스트룸-리우빌 연산자는 자기수반성을 갖고 있습니다. 이로부터 증명을 시작할 수 있습니다.

증명을 이어나가기 위해 내적을 표현해보겠습니다. 그리고 고윳값 문제 관계를 이용해서 식을 변형했습니다.

이와 비슷하게 오른쪽 항의 내적도 표현할 수 있습니다.

이제 두 내적 결과가 같음을 이용하여 관계성을 살펴보겠습니다.

같은 고유함수(eigenfunction)에 대한 내적 결과는 0이 될 수 없습니다. 그렇기에 고윳값과 그 켤레의 형태가 같아야만 자기수반성이 설명됩니다. 어떠한 값과 그의 켤례형태가 동일하다는 것은 해당 값이 실수(real)임을 의미합니다. 따라서 스트룸-리우빌 연산자에 대한 고윳값은 항상 실수인 것을 알 수 있습니다.

증명과는 별개의 이야기이지만, 어떠한 연산자의 고윳값이 실수인 사실은 물리에서 중요한 특성 중 하나입니다. 어떠한 함수의 연산자를 취하는 것은 특정 함수로부터 원하는 정보를 특정하여 관측하겠다는 것을 의미합니다. 실제 우리가 관측하는 정보들은 모두 실수인데, 만약 연산자의 결과가 허수라면 현상을 이해하는데 어려움이 생길 것입니다. 그렇기에 이용하고자 하는 연산자가 에르미트 연산자임을 알고 있다면 이를 관측에 적극적으로 사용할 수 있다는 이점이 있습니다.

Contents Preview

스트룸-리우빌 연산자가 자기수반성을 가짐을 보이며, 사실은 이 연산자가 에르미트 연산자(Hermitian Operator)임을 보일 것입니다.

스트룸-리우빌 연산자는 특정 공간 안에서 자기수반성을 갖습니다. 이를 증명하도록 하겠습니다.

<증명 1> 일반적인 경계조건에 대한 스트룸-리우빌 연산자의 자기수반성

본격적인 증명에 앞서 한가지를 살펴보겠습니다. 연산자를 각기 다른 함수에 취했을 때 그 내적 결과가 같을 때, 우리는 이 연산자가 자기수반성을 갖는다고 말할 수 있습니다. 하지만, 우리는 어떠한 연산자를 켤레화하고(Conjugation) 전치(Transpose)했을 때에도 기존의 연산자와 같을 때 자기수반성을 갖는다고 알고 있습니다. 내적을 이용해서 위처럼 증명을 시작해도 자기수반성임을 보일 수 있는지 살펴보겠습니다.

이처럼 켤레화를 했을 때 연산자의 위치가 변하고, 이를 이용하면 내적을 이용해서도 자기수반성을 표현할 수 있게 됩니다, 계속 증명을 이어나가겠습니다.

각각의 내적을 진행했고, 그 결과를 얻을 수 있었습니다. 식을 정리하기 위해서 부분적분법(Integrate by parts)를 이용한 것을 확인할 수 있습니다. 이제 이 둘 이 같아질 수 있음을 확인하기 위해 두 항을 빼보겠습니다.

만약 두 내적의 차가 0이였다면 우리는 바로 증명을 마칠 수 있었을 것입니다. 하지만 어떠한 값들의 조합이 결과로 나온 것을 확인할 수 있습니다. 이를 소거하기 위해서 우리는 경계조건(boundary condition)을 확인해야 합니다. 우선, 일반적인 제차의 경계조건(homogeneous Boundary Condition을 설정해보겠습니다.

그리고 이 경계조건을 켤례화할 수 있습니다. 켤례화를 한다고 하더라도 제차 형태의 식이므로 값에는 변동이 없을 것입니다.

주어진 조건, 그리고 켤례화한 조건을 변형하여 관계식을 얻을 수 있습니다.

이를 식 (*)에 대입하여 정리할 수 있고 그 결과는 다음과 같습니다.

<증명 2> 특수한 형태의 경계조건에 대한 스트룸-리우빌 연산자의 자기수반성

만약 경계조건의 계수가 0을 포함하고 있어 어떠한 유리식의 형태로 식을 정리할 수 없는 경우도 있을 것입니다. 이때에도 해당 증명은 성립하며, 각 조건에 대해 살펴보겠습니다.

(1) Dirichlet Boundary Condition

이 조건에서는 변화 정도를 표현하는 계수 d가 0입니다. 이를 이용해서 조건을 다시 쓸 수 있고, 식을 정리할 수 있습니다.

(2) Neumann Boundary Condition

이 조건에서는 상태를 표현하는 계수 c가 0입니다. 마찬가지로 조건을 다시 작성하고, 식을 정리하여 자기수반성을 보일 수 있습니다.

(3)  Periodic Boundary Conditon

한편, 주기성을 보이는 경계조건에 대해서도 자기수반성이 성립하는데, 이를 보이면 다음과 같습니다.

지금까지 스트룸-리우빌의 자기수반성 증명을 살펴보았습니다. 이 특성은 스트룸-리우빌 연산자는 자기수반성을 가지며, 이 연산자를 에르미트 연산자로 생각할 수 있음을 나타냅니다. 에르미트 연산자의 특성을 공유합니다. 다음 글들에서는  여러 특성들 중에서 중요한 특성 2가지에 대해 더 알아보도록 하겠습니다.

Contents

1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)

- 미분방정식을 풀이하는 데 있어 필요한 조건들에 대해 간략히 소개합니다. 초기 시점에 비중을 둔 초기조건과 공간에 비중을 둔 경계조건에 대해 설명을 드리고자 합니다. 주어진 미분방정식의 해를 특정하기 위해 필요한 조건의 개수에 대해 논의해보고, 물리학에서 경계조건의 중요성에 대해서도 말씀드리겠습니다.

2. 경계조건의 분류 (the Classification of Boundary Condition)

- 경계조건을 구분하는 것은 생각보다 중요한 일인데, 이러한 이유와 경계조건의 종류를 살펴보겠습니다. 

0. Introduction - 조건설정의 필요성 (the Necessity of Setting Conditions)

본격적인 내용에 들어가기 앞서 한가지 내용을 먼저 같이 생각해보려 합니다. 우리는 왜 미분방정식을 풀이하는 것에 대해 배워야 할 필요가 있을까요? 여러 이유를 들 수 있습니다. 제 생각에는 지배방정식(Governing Equation)을 풀이하기 위해 미분방정식을 공부해야 한다고 생각합니다. 

지배방정식은 어떠한 상황에서 알고 있는(또는 측정할 수 있는) 변수들과 우리가 알고 싶은(또는 측정해야 하는) 변수들 사이의 관계를 나타내는 식입니다. 이들은 특정 시점($t$)과 미소 시간이 흐른 시점($t+dt$) 사이의 물성 변화로부터 얻어지기 때문에 미분방정식의 형태를 띠는 경우가 많습니다. 수지 방정식(Balance Equation), fin에 대한 열전도 방정식(Heat Conduction) , 1D Box에 놓여있는 입자의 파동방정식(Wave Equation) 등을 예로 들 수 있습니다. 이러한 방정식들을 풀이해야 우리가 원하던 정량적인 정보를 얻을 수 있습니다. 그렇기에 학부수준의 문제를 해결하기 위해서는 미분방정식을 다룰 수 있어야 한다고 생각합니다. 

지배방정식들은 놓여있는 조건(상황)에 따라 그 해가 매우 상이합니다. 추후에 같이 살펴보겠지만, 같은 대류현상에 대한 지배방정식을 풀이하더라도 주변이 단열되어있는지, 아니면 일정하게 가열되고 있는지에 따라 편미분방정식의 형태는 매우 다르게 나타납니다. 따라서 우리는 지배방정식에 대한 조건을 올바르게 설정할 수 있어야 합니다.

조건은 크게 2가지로 분류됩니다. 관측시점을 중요시 하는 초기조건(Initial Condition)과 관측위치를 중요시 하는 경계조건(Boundary Condition)이 있습니다. 이제 조건에 대해 본격적으로 얘기해보겠습니다.

1. 초기조건과 경계조건 (Initial Condition and Boundary Condition)

1) 초기조건 (Initial Condition)

초기조건은 어떠한 미분방정식에서 특정 시점에 대한 해의 정보들의 집합을 의미합니다. 초기조건은 시간에 대한 물성 변화를 설명할 때 사용되며, 물체 관측의 시작점($t=0$)에서의 정보를 표현하는 경우가 많습니다. 수식으로 표현하면 다음과 같습니다.

초기조건은 주로 상미분방정식, 또는 편미분방정식 중 시간과 관련된 정보를 결정하는 데 사용됩니다.  $n$차 상미분방정식을 결정하기 우해서는 $n$개의 초기조건이 필요합니다. 

2) 경계조건 (Boundary Condition)

경계조건은 특정 위치에 대한 해의 정보들의 집합을 의미합니다. 경계조건은 장소(위치)변화에 대한 물성을 표현할 때 사용합니다. 주로 검사체적(Control Volume, system)과 주변(Surrounding)을 구분짓는 경계표면(Control Surface)에 대한 정보들이 주로 나타납니다. 만약 물체가 1D에 놓여있다면 수직선 양 끝 정보가, 3D에 놓여있다면 체적의 표면들에 대한 정보가 표현되어 있을 것입니다. 1D Differential Equation에 대한 경계조건을 수식으로 표현하면 다음과 같습니다. 

한번 언급했듯, 편미분방정식의 해는 시공간에서의 물성의 분포를 표현합니다. 그렇기에 편미분방정식에서의 경계조건에 대한 중요성은 매우 높습니다. 

3) 해 결정을 위해 필요한 조건의 개수

적절한 종류의 조건을 사용하는 것도 중요하지만, 적합한 해를 찾기 위한 조건의 개수를 아는 것도 중요합니다. 조건의 개수를 너무 많이 부여하면 과적합한 해가 얻어지고, 부족한 개수의 조건을 설정할 경우 해가 정해지지 않습니다.

적합한 해의 개수를 결정하기 위해서는 미분된 변수의 종류와 최고 미분된 횟수를 고려하면 됩니다. 시간에 대한 미분의 차수와 공간에 대한 미분의 차수를 파악한 후 시간에 대한 미분에는 초기조건을 부여하고, 공간에 대한 미분에는 경계조건을 설정하면 됩니다. 예를 들어 보겠습니다.

어떤 편미분 방정식이 시간에 대해 1차 미분, 공간에 대해 2차 미분이 되어있다면 1개의 초기 조건과 2개의 경계조건이 필요합니다.

미분은 정보를 소거하는 연산이고, 적분은 정보를 확장하는 연산입니다. 미분방정식을 푼다는 것은 결국 적분을 거쳐 해를 얻는 것을 의미하기에, 미분된 횟수만큼 적분을 해주어야 합니다. 이는 미분된 횟수만큼의 조건을 필요로 한다는 것으로 해석할 수 있습니다.

예를 들어 보겠습니다.

이 미분방정식은 등가속도 운동을 표현하는 간단한 형태의 미분방정식입니다. 이를 풀이하는 과정은 아래와 같습니다.

미분방정식은 풀이했지만 아직 조건이 충분히 제시되지 않았습니다. 2계 상미분방정식의 풀이를 위해서 2번 적분한 것을 확인할 수 있을겁니다. $A_0$과 $B_0$이 결정되어야 우리가 원하던 특정한 해를 얻을 수 있는 것입니다. 2개의 적분상수가 결정되어야 하므로 2개의 조건이 필요합니다. 이 문제는 측정할 수 있는 시점에서의 수치를 기반으로 정보를 확장하는 것이므로 초기조건을 설정하여 해를 특정하겠습니다. 

이 결과 해는 다음과 같이 표현됩니다.

이 물리적 현상을 관통하는 지배방정식에 조건을 설정하여 풀이했더니 하나의 특정한 해를 얻은 것을 확인할 수 있었습니다. 

이 문제에 다른 조건을 설정해서 풀어보겠습니다. 이번에는 경계조건을 걸어보겠습니다. 편하게 논의하기 위해 공간과 관련된 항에 경계조건을 설정하라고 이야기했지만, 좀더 구체적인 경계조건의 표현은 아래와 같습니다.

"경계조건은 정의역의 양 끝 지점에서의 해와 관련된 정보를 제시한 것"

즉  경계조건은 외부의 영향을 직접적으로 받는 지점에서의 정보가 제시된 것임을 알 수 있습니다. 한번 살펴볼까요?

정의역이 $t\in[0,1]$일 때 경계조건이 다음과 같다고 생각해보겠습니다. 이를 해에 대입했을 때 적분상수를 계산할 수 있습니다.

이제 특정한 해를 표현하고 이용할 수 있습니다.

요약하자면 미분방정식의 해를 특정하기 위해서는 조건이 필요하고, 그 개수는 독립변수에 대한 최대 미분 횟수와 동일합니다. 

4) 물리학에서 경계조건의 중요성

경계조건은 물리학/공학에서 큰 중요도를 가집니다. 경계에 대한 정보를 갖고 지배방정식을 풀이할 수 있다면 정의된 영역에 대한 모든 정보를 예측할 수 있기 때문입니다. 예를 들어 2D Plate에 대한 문제를 해결해야 한다고 생각해봅시다. 그렇다면 각 변에서의 물성에 대한 정보만 알고 있으면, 2D Plate 전 영역에 대한 물성의 정보를 예측할 수 있다는 것을 의미합니다. 즉, 부분의 정보로부터 전체의 정보를 이끌어내는 것을 가능하게 해주는 것이 경계조건 입니다.

경계는 실험자에게도 유리한 지점입니다. 바로 측정이 가능한 위치이기 때문입니다. 당장 정육면체 내부의 온도 분포를 조사한다고 했을 때, 정육면체 중심보다는 각 면에다가 온도 조절 장치를 설치하는 것이 유리할 것입니다.

실험 설계 측면에서도, 해의 결정에 있어서도 경계조건은 중요한 것은 당연합니다.

2. 경계조건의 분류 (the Classification of Boundary Condition)

편미분방정식을 풀이할 때 유의해야 하는 점이 있습니다. 편미분방정식의 종류에 따라 특정한 해를 얻을 수 있는 경계조건의 형태가 정해져있습니다. 그렇기에 경계조건을 꼭 분류할 수 있어야 합니다. 특히 스투름-리우빌 문제를 풀이하는 데 필요한 경계조건을 일반화해서 표현할 수 있는데, 이는 다음과 같습니다.

이를 물리적으로 해석해볼 수 도 있겠습니다. $y(a)$는 경계에서의 물리량이 일정하다는 것을 의미합니다. 예를 들어 일정한 온더를 유지하는 열원(Heat Reservior)이 있을 수 있습니다. 반면에 $y'(a)$는 경계에서 물리량의 변화가 일정하다는 것을 의미합니다. 예를 들면 유체의 흐름(flux)가 경계표면에서 일정한 상황을 생각해볼 수 있습니다. 결국 경계조건은 물성에 대한 특정 값 또는 변화량을 포함하고 있을 수 있음을 시사합니다. 계수 $\alpha, \beta, m, n$의 유무에 따라 경계 조건의 종류가 달라집니다.

(1) Dirichlet BC

이 경계조건은 경계지점에서의 물리량들의 값이 제시된 조건을 의미합니다. 즉, 변화를 나타내는 값들의 계수인 $m, n$이 0이 되는 상황을 얘기하는 것입니다. 

(2) Neumann BC

이 경계조건은 경계지점에서의 도함수(또는 변화) 정도가 제시된 조건입니다. 즉, 일정한 값을 나타내는 항들의 계수인 $\alpha, \beta$가 0이 되는 상황을 뜻합니다.

(3) mixed Dirichlet-Neumann BC (or Cauchy BC)

이 경계조건은 특정 물리량과 물리량의 변화 정도가 모두 제시된 경계조건입니다.

(4) periodic BC

이 경계조건은 경계지점에서의 물리량이 동일하고, 해당 수치들이 주기적으로 나타나는 조건입니다. 예를 들면 다음과 같습니다.

한편, 위에서 조건들이 갖는 값 $A, B$가 모두 0이라면 이 조건은 제차(homogeneous)라고 하고, 그렇지 않다면 비제차(Inhomogeneous)라고 합니다. 제차 경계조건이 제시된 경우 해를 표현하기 편리하기 때문에 제체화를 할 수 있어야 합니다. 이는 추후 비제차 경계조건이 할당된 편미분방정식을 풀이할 때 같이 살펴보겠습니다.

스투름-리우빌 정리를 공부하다가 갑자기 경계조건에 대해 장황하게 이야기를 한 이유에 대해 궁금할 수 있다고 생각합니다. 이는 바로 다음 글에서 살펴볼 스투름-리우빌 미분방정식의 해의 직교성(Orthogonality)를 보일 때, 경계조건에 대한 논의가 필수적이기 때문입니다. 해당 내용을 다룰 때 다시 한번 설명하겠습니다.

Contents

1. 스투름-리우빌 미분방정식의 개념과 형태 (The Concept and Formula of Sturm-Liouville Differential Equation)

- 스투름-리우빌 미분방정식(Sturm-Liouville Differential Equation)의 개념, 편미분방정식의 풀이를 위해 이 이론이 유효한 이유, 수학적 형태에 대해 같이 생각해볼 것입니다.

2. 스투름-리우빌 연산자와 고윳값 문제 (The Sturm-Liouville Operator and the Eigenvalue Problem)

- 스투름-리우빌 미분방정식의 형태를 조작해서 이 문제가 결국 선형대수학에서 주로 다루던 고윳값 문제(eigenvalue problem)임을 보여보고자 합니다. 그리고 스투름-리우빌 문제를 다루기 위해 필요한 선형대수적 지식을 간단하게 다루어보겠습니다.

1. 스투름-리우빌 미분방정식의 개념과 형태 (The Concept and Formula of Sturm-Liouville Differential Equation)

1) 스투름-리우빌 이론의 필요성 (the Necessity of Sturm-Liouville Theory)

스투름-리우빌 이론은 임의의 2차 선형 상미분방정식(the 2nd order linear ODE)에서 해를 얻을 수 있음을 말하며, 얻어낸 해의 특성들을 설명합니다.

우리가 편미분방정식(PDE)을 공부하고 있음에도 불구하고 2차 상미분방정식과 관련된 내용을 알아두어야 하는지에 대해 얘기해보고자 합니다. 편미분방정식을 관통하는 풀이원리는 아직 밝혀지지 않았습니다. 풀이를 할 수 있는 몇가지 전략들이 있는데 그 중 하나가 변수분리법(Separation of Variables)입니다. 이 방법은 하나의 편미분방정식 문제를 여러개의 상미분방정식 풀이로 바꾸어줍니다. 공학이나 물리학에서는 주로 2차 편미분방정식을 사용합니다. (변수에 대한 최대 미분횟수가 2회인 편미분방정식을 의미합니다.) 그렇기에 변수분리법을 통해 얻은 상미분방정식들은 2차인 경우가 많습니다. 요약하자면, 하나의 편미분방정식 풀이가 변수분리법에 의해 여러개의 상미분방정식, 특히 2차  ODE의 풀이로 바뀌기 때문에 2차 선형 상미분방정식에 대한 이해가 필요한 것입니다. 

2) 스투름-리우빌 미분방정식의 형태 (the Formula of Sturm-Liouville Differential Equation)

이제 스투름-리우빌 미분방정식의 형태를 알아보겠습니다. 

위와 같이 표현될 수 있는 2차 선형 상미분방정식을 스투름-리우빌 미분방정식입니다. $p(x)$는 이계도함수가 존재해야 위의 식을 풀이할 수 있습니다. $q(x)$에는 특별한 조건이 필요하지 않습니다. 여기서 $r(x)$는 모든 2차 선형 상미분방정식을 스투름-리우빌 미분방정식 형태로 바꾸어주는 가중치함수(weight function)입니다. 조금 있다가 스투름-리우빌 연산자를 이야기할때 같이 다뤄보겠습니다.

2. 스투름-리우빌 연산자와 고윳값 문제 (The Sturm-Liouville Operator and the Eigenvalue Problem)

1) 스투름-리우빌 연산자 (Sturm-Liouville Operator)

이 미분방정식을 푸는 것은 단순히 해 $y$만 구하는 것이 아니라, 이를 특정짓는 고윳값(eigenvalue) $\lambda$도 같이 구하는 것입니다. 그렇기에 이 미분방정식은 결국 고윳값문제에 해당합니다. 이를 위해 위의 스트룸-리우빌 미분방정식을 변형하겠습니다.

위의 식으로부터 고윳값 문제 형태를 얻어내기 위해 미분연산자에 포함되어 있던 $y$를 분리한 것입니다. 선형대수학에서 배웠던 기억을 떠올리면 위의 형태를 고윳값 문제로 표현할 수 잇습니다. 그 결과는 아래와 같습니다.

이때 여기서 정의한 $L$을 스투름-리우빌 연산자(Sturm-Liouville Operator)라고 합니다. 스투름-리우빌 연산자는 여러가지 특성을 갖고 있는데, 이는 추후에 다루어보기로 하고 지금은 다른 이야기를 먼저 해보려 합니다.

2) 제차 2차 선형 상미분방정식과 스투름-리우빌 미분방정식 사이의 관계 : 동치

스투름-리우빌 문제의 매력적인 점은 '임의의 2차 상미분방정식'을 모두 스투름-리우빌 미분방정식으로 표현하여 해의 특성에 대해 미리 예측하고 성질을 파악할 수 있다는 점입니다. 이 글에서는 제차 2차 선형 상미분방정식(homogeneous 2nd order linear ODE)이 어떻게 스트룸-리우빌 미분방정식으로 표현될 수 있는지를 살펴보겠습니다.

고윳값 문제를 다시 작성하겠습니다.

2차 상미분방정식 문제이므로 미분연산자들을 조합한 새로운 연산자 $L$을 이용해서 위의 문제를 표현한 것입니다. 이제 위 식의 형태를 변형하여 2차 선형 상미분방정식이 모두 스투름-리우빌 미분방정식의 형태를 가질 수 있음을 보이겠습니다.

(1) $p^{(1)}_0(x)=p_1(x)$인 경우

이 경우에 대해 식이 어떻게 정리되는지 살펴보겠습니다.

곱의 미분(product differential)에 의해서 연산자를 다음과 같이 정리할 수 있습니다. 고윳값 문제에 대입해보겠습니다.

$p_0$과 $p_2$는 제약이 딱이 없었기 때문에 이를 잘 조종하면 스투름-리우빌 미분방정식의 형태로 식을 변형할 수 있습니다. 이 경우에는 가중치함수 $r(x)=1$로 별다른 영향이 없는 것을 확인할 수 있습니다.

(2) 일반적인 제차 2차 선형 상미분방정식과 스투름-리우빌 미분방정식 : 가중치함수의 결정

(1)의 경우는 매우 특수한 경우입니다. 해당 조건이 성립하지 않는 미분방정식이 훨씬 많을 것입니다. 그럼에도 불구하고 일반적인 제차 2차 선형 상미분방정식을 스투름-리우빌 미분방정식으로 형태를 바꿀 수 있습니다. 가중치함수(weight fucntion)를 이용할 때 이와 같은 변환이 가능합니다. 가중치 함수 $r(x)$는 2가지 특성을 갖습니다.

$<f,g>_r$은 가중치함수를 고려한 내적(inner product)인데, 해당 내적의 값이 존재하여, 적분이 가능해야 합니다.

이제 가중치 함수를 이용해서 일반적인 미분연산자를 스투름-리우빌 연산자로 조작하는 법을 살펴보겠습니다. 이 변환의 전제는 '가중치 함수를 곱했을 때 해당 미분방정식은 반드시 스투름-리우빌 미분방정식의 형태로 변환될 수 있다'입니다. 즉, 우리는 당면한 미분방정식을 변환할 수 있는 가중치 함수를 결정할 수 있어야 합니다.

원래의 고윳값 문제에서 가중치 함수를 곱하면 다음과 같습니다.

그리고 새롭게 표현된 미분연산자를 표현할 수 있습니다.

이때 해당 미분연산자가 결국 스투름-리우빌 연산자로 변환이 가능함을 전제로 하기 때문에 해당 조건이 만족할 것입니다.

이 관계를 이용하면 가중치 함수 $r(x)$를 구할 수 있을 것입니다. 과정을 같이 살펴보겠습니다. 

$r(x)$를 결정하기 위해서 변수분리법을 이용할 것입니다. 이를 위해서 좌측항에는 $r$에 대한 식을 우측항에는 $p(x)$에대한 식을 모아 정리했습니다. 적분을 마저 진행하겠습니다.

우리가 얻은 가중치 함수 $r(x)$를 곱하면 임의의 미분방정식도 스투름-리우빌 미분방정식의 형태로 바꿀 수 있음을 알게 되었습니다. 연산자를 이용해서 마저 표현해보겠습니다.

$r(x)p_0(x)$와 $r(x)p_2(x)$를 적절하게 조정하면 결국 스투름-리우빌 미분방정식에서 얻어낸 고윳값 문제로 바꿀 수 있게됩니다. 

요약하자면, 임의의 2차 선형 상미분방정식은 모두 스투름-리우빌 문제로 바꾸어 표현할 수 있으며, 이 포스팅에서는 제차 2차 선형 상미분방정식에 대해 논의를 한 것입니다.

Contents

1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)

푸리에 변환의 형태와 대칭성이 고려되었을 때의 푸리에 변환을 같이 살펴보겠습니다.

2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)

푸리에 변환이 갖는 몇가지 대수적 특성들에 대해 살펴볼 것입니다.

3. 파르스발 이론 (Parseval's Theorem)

함수와 푸리에 계수 사이의 관계를 설명하는 파르스발 이론에 대해 살펴보고, 이 이론이 가져다주는 의의에 대해 간략하게 살펴볼 것입니다.

1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)

1) 푸리에 변환의 의의

푸리에 변환은 주기성을 갖는 함수들에만 적용 가능했던 푸리에 급수의 단점을 극복한 적분 변환 기법입니다. 그 결과 이 변환법은 다양한 분야에서 사용되게 됩니다. 그 중에서도 통신에 대해 공부하는 사람들은 푸리에 변환을 수없이 살펴보게 될 것입니다. 푸리에 변환을 통해 시간 영역에서 정의된 함수를 주파수 영역으로 전사(mapping)하여 여러 해석을 용이하게 돕습니다.

2) 푸리에 변환의 수학적 형태

(1) 푸리에 변환의 관계와 형태

푸리에 변환 $F$에 대해 원함수와 변환된 함수는 아래의 관계를 갖습니다.

어떠한 함수에 푸리에 변환($F$)을 취하면 주파수 함수를 얻을 수 있으며, 반대로 푸리에 역변환($F^{-1}$)을 취하면 원래의 함수를 얻을 수 있습니다.

푸리에 변환과 역변환의 수학적 형태는 다음과 같습니다.

어떠한 함수에 $F$또는 $F^{-1}$를 취했을 때 사용자가 원하는 함수를 얻는 것을 알 수 있습니다.

(2) 대칭성을 갖는 함수에 대한 푸리에 변환

만약 푸리에 변환을 취하려는 함수가 기함수 또는 우함수라면 푸리에 변환을 특수하게 표현하며, 이를 푸리에 사인/코사인 변환(Fourier Sine/Cosine Transformation)이라고 합니다. 만약 원래 함수가 기함수라면 푸리에 사인 변환을, 우함수라면 푸리에 코사인 변환을 취할 수 있습니다. (푸리에 급수와 유사한 것을 알 수 있습니다.) 각 변환의 수학적 형태를 살펴보겠습니다.

푸리에 사인 변환 (Fourier Sine Transformation)

푸리에 코사인 변환 (Fourier Cosine Transformation)

원래의 푸리에 변환과 약간 형태가 상이하여 의문을 가질 수도 있다 생각됩니다만, 결국 똑같습니다. 왜냐하면 대칭성에 의해 적분 구간을 반으로 줄이더라도 적분값을 2배로 하면 그 결과가 같기 때문입니다. (일전에 대칭성을 갖는 함수의 푸리에 급수를 다뤄보며 언급했으므로 참고하시면 될 것 같습니다.)

2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)

푸리에 변환의 몇가지 특성을 알아보기 위해 한 가지 약속을 하겠습니다. $f(x)$와 $g(x)$는 각각 푸리에 변환을 취할 수 있는 함수이며, 그 관계는 아래와 같습니다.

이 약속을 전제하고 푸리에 변환의 수학적 특성을 설명하겠습니다.

1) 선형성 (Linerarity)

푸리에 변환은 라플라스 변환과 마찬가지로 선형 연산자입니다. 선형성은 가산성(additivity)와 동차성(homogeneity)이 동시에 성립할 때 보장됩니다. 이는 적분 자체가 선형적인 연산자이기 때문인데, 이를 수학적으로 표현하면 다음과 같습니다. 

선형성은 푸리에 변환에 $f(x)$대신 $af(x)+bg(x)$를 대입한 후, $f$와 $g$에 대한 푸리에 변환으로 분리하면 쉽게 얻어낼 수 있습니다. 

2) 도함수에 대한 푸리에 변환 (Fourier Transformation of Derivatives)

n번 미분할 수 있는 어떠한 함수 $f$에 푸리에 변환을 취할 수 있습니다.

이 성질은 수학적 귀납법을 이용해서 증명을 할 수 있습니다. 자세한 증명 과정은 생략하고, 기회가 될 때 다루어보겠습니다.

3) 푸리에 변환의 합성곱 (Convolution of Fourier Transformation)

라플라스 변환에서와 마찬가지로 푸리에 변환에 대한 합성곱(Convolution)을 정의합니다. 형태는 다음과 같ㅅ브니다.

이를 이용했을 때 푸리에 변환된 서로다른 두 함수가 곱해져있을 때, 푸리에 역변환을 취해서 원래의 함수를 얻을 수 있습니다. 

증명 방법은 라플라스 변환의 합성곱과 동일하며, 증명 과정은 따로 자세히 설명하지 않겠습니다.

3. 파르스발 이론 (Parseval's Theorem)

1) 파르스발 이론과 푸리에 급수 (Parseval's Theorem and Fourier Series)

푸리에 급수에 대해 파르스발 이론은 푸리에 급수는 계수들의 정보로 표현될 수 있음을 뜻합니다. 정확히 얘기하자면 주기 함수의 내적(inner product)은 푸리에 계수 사이의 내적과 일정한 관계를 보입니다. 

$f(x)$와 $g(x)$가 동일한 주기를 $T$로 갖는 주기함수라고 하고, 복소지수함수를 포함한 푸리에 급수에서의 푸리에 계수를 각각 $c_k$, $d_k$라고 하겠습니다. 이때, 두 함수 사이의 내적은 푸리에 계수 사이의 내적과 일정한 관계를 갖습니다.

이때 $f(x)=g(x)$인 상황을 생각해보면, 다른 의미를 얻을 수 있습니다. 이 경우 같은 함수의 내적을 통해 얻은 함수의 크기가 결국 계수의 크기와 동일하다는 것을 알 수 있게 됩니다. 식으로는 다음과 같이 표현할 수 있습니다.

2) 파르스발 이론과 푸리에 변환 (parseval's Theorem and Fourier Transformation)

푸리에 변환에서의 파르스발 이론도 결국 동일한 이야기를 합니다. 간단히 설명하고 넘어가겠습니다.

여기까지가 편미분방정식을 본격적으로 시작하기 전에 간략하게나마 다루어본 푸리에 급수와 푸리에 변환 내용입니다. 푸리에 변환에 대한 전반적인 내용이 필요 없더라도 푸리에 급수에서 푸리에 계수 정보를 얻어내기 위해 내적과 직교성을 이용한 방법은 꼭 숙지하셨으면 좋겠습니다. 편미분방정식의 해를 특정하는 데에도 동일한 방법이 사용되기 때문입니다. 복습을 위해 

다음부터는 스트룸-리우빌 정리(Strum-Liouville Theory)와 초기/경계조건(Initial/Boundary Condition)에 대해서 살펴보겠습니다.

Contents

1. 실수형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

- 실수 형태로 표현된 푸리에 급수를 이용해서 푸리에 적분을 표현하는 방법에 대해서 알아볼 것입니다.

2. 복소형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

- 복소지수함수 형태로 표현된 푸리에 급수를 이용해서 푸리에 적분을 표현하는 방법에 대해서 알아볼 것입니다.

 지금까지 우리는 푸리에 급수 공부해왔습니다. 푸리에 급수는 표현하려는 함수가 주기함수여야 한다는 가정 아래 논의되었습니다. 하지만 우리가 다루게 될 많은 함수들은 주기를 갖지 않습니다. 주기도 관찰되지 않으며 해석도 어려운 함수를 다루기 위해서 푸리에 급수를 더 발전시키게 됩니다. 어떠한 주기함수에 대해서 해당 주기를 무한대까지 극한을 보내는 방법을 사용합니다. 즉, 주기의 크기가 무한대에 수렴하는 푸리에 급수를 구하는 것을 뜻합니다. 이를 푸리에 적분(Fourier Integral)이라고 합니다.

푸리에 급수는 실수형태로 정의되거나 허수를 포함한 지수함수의 형태로 표현되었습니다. 그렇기에 각각의 형태로부터 푸리에 적분을 유도하는 과정에 대해 살펴보겠습니다.

1. 실수형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

푸리에 급수로 표현 가능하고 구간 $[-T/2,T/2]$에서 정의된 함수 $f(x)$가 있다고 해보겠습니다. $f(x)$에 대해 푸리에 급수를 작성하겠습니다.

이때 계산상의 편의를 위해 아래의 변수를 정의하겠습니다. 그러면 아래의 관계도 성립하는 것을 알 수 있습니다.

실제로 푸리에 급수가 어떻게 계산되는 지를 파악하기 위해 푸리에 계수를 푸리에 급수에 실제로 대입해보겠습니다. 복잡한 표기를 피하기 위해 위에서 정의한 새로운 변수도 이용하겠습니다.

이제 이 함수의 주기 $T$를 무한대로 보내 하나의 함수로 만들 것입니다. 함수 하나를 정의하겠습니다.

이 함수는 푸리에 급수를 적용할 수 있는 함수의 주기를 무한대로 보내어 주기함수가 아닌 하나의 함수를 정의한 것입니다. 주기를 극한으로 보낼 때 푸리에 급수가 수렴하려면 하나의 가정이 필요합니다. 함수 $f(x)$의 적분결과가 유한하다는 것입니다. 이를 수학적으로 표현할 수 있습니다.

이 가정은 시그마 안에 있는 두 적분항들도 적분이 가능하다는 것을 설명합니다. 이는 삼각함수의 치역때문인데, 아래의 부등식에 표현하겠습니다.

삼각함수의 절댓값은 1보다 클 수 없기 때문에 해당 관계식이 성립하며, 부등식의 삼단 논법에 의해 $f(x)$의 적분 유한성이 확장되어 적용될 수 있습니다. 예시로 코사인함수를 사용했지만, 사인함수의 경우도 결과가 동일하기에, 푸리에계수는 모두 적분이 가능하다는 것을 알 수 있습니다.

적분구간을 고려하여 무한에 가까운 주기를 갖는 함수에 대한 각각의 푸리에 계수를 정의할 수 있습니다.

이 결과들을 종합하여 무한대에 가까운 주기를 갖는 함수에 대한 푸리에 급수를 표현하면 다음과 같습니다.

이때 시그마 기호 안에 묶여있는 삼각함수를 하나의 함수로 본다면 주어진 부분합의 극한을 리만 적분(Rimann Integral)으로 표현할 수 있습니다. (자세한 내용은 미적분학을 참고하면 알 수 있습니다.) 그 결과는 다음과 같습니다.

푸리에 급수를 공부할 때 모든 함수는 우함수와 기함수로 표현될 수 있음을 공부했습니다. 푸리에 적분을 이용해서 함수를 표현해도 이 내용은 동일할 것입니다. 

이때 주어진 함수가 짝수일 때 얻어지는 푸리에 적분을 푸리에 코사인 적분(Fourier Cosine Intergral)이라고 하며, 홀수 함수일 때 얻는 푸리에 적분을 푸리에 사인 적분(Fourier Sine Integral)이라 합니다.

2. 복소형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

본격적인 적분에 앞서 복소지수함수형태를 포함한 푸리에 급수의 형태를 다시 한번 살펴보겠습니다.

함수의 주기를 확장하기 위해 새롭게 함수를 정의하고, 이에 대해 푸리에 급수를 다시 작성할 수 있습니다.

실수형태에서의 푸리에 적분을 구하는 것과 마찬가지로 푸리에 계수를 급수식에 대입한 후 식을 전개하겠습니다.

마찬가지로 몇가지 변수를 새로이 정의하고, 이를 이용해서 다시 함수를 표현하겠습니다.

논의를 위해 함수 $f(x)$가 적분 가능하다고 하겠습니다. (구체적인 설명은 실수로 표현된 푸리에 적분을 참고하시면 되겠습니다.) 편한 표기를 위해 푸리에 계수를 정의하겠습니다.

이 형태는 추후 알게되겠지만 푸리에 변환(Fourier Transformation)의 형태입니다. 이를 이용해서 푸리에 적분을 마저 얻어내겠습니다. 

Contents

1. 실수 형태의 푸리에 급수에서 복소 형태로의 전환 (Transformation from Real Form to Complex Form)

- 오일러 항등식(Euler's Identity)을 이용해서 실수 형태로 표현된 푸리에 급수를 복소수를 포함한 형태로 전환하는 과정에 대해 살펴보겠습니다.

2. 복소지수함수를 포함한 푸리에 계수의 결정 (Determinant of Fourier Coefficient in the form of Complex Number)

- 오일러 항등식을 이용하면 자연상수를 포함한 형태로 푸리에 급수가 표현됩니다. 이때 표현되는 푸리에 계수를 내적(Inner Product)를 이용해서 구하는 방법에 대해 살펴볼 것입니다. 실수 형태의 푸리에 급수와 동일하게 직교성을 활용하여 구하는 것을 확인할 수 있을 것입니다.

1. 실수 형태의 푸리에 급수에서 복소 형태로의 전환 (Transformation from Real Form to Complex Form)

물리학을 다룰 때, 복소수를 차용해서 수식을 표현하는 경우가 많이 있습니다. 오일러 항등식(Euler's Identity)은 실수와 복소수 사이의 관계를 표현하는 대표적인, 그리고 가장 유명한 항등식입니다. 이 수식은 다음과 같습니다.

푸리에 급수를 다시 한 번 살펴보겠습니다. 

푸리에 급수는 삼각함수의 조합을 통해서 어떠한 함수를 비슷하고, 계산에 용이하게 바꾸어 표현하기 위해 정의되었습니다. 그렇기에 그 식은 코사인 함수와 사인 함수를 포함합니다. 오일러 항등식을 변형해서 코사인 및 사인 함수를 자연상수를 이용해서 표현한다면 실수 형태로 정의된 푸리에 급수를 허수를 포함한 형태로 바꾸어 표현할 수 있게 될 것입니다.

$\theta$에 $-\theta$를 대입하면 오일러 항등식의 파생 형태를 얻을 수 있으며, 이를 이용하면 코사인과 사인에 대한 식을 얻어낼 수 있습니다. 약간의 연립방정식만 풀이하면 되므로 중간 계산 과정은 생략하겠습니다. 새롭게 얻은 관계를 표현하면 아래와 같습니다.

이를 이용해서 푸리에 급수에서 사용된 삼각함수를 자연상수의 형태로 먼저 변환하겠습니다. 결과는 다음과 같습니다.

위의 관계를 이용해서 실수 형태의 푸리에 급수의 변환을 시작하겠습니다.

 동일한 지수함수 형태끼리 식을 묶어주어 정리할 수 있습니다.

편한 표기를 위해서 지수함수 앞의 계수를 $c_k$로 정의하겠습니다. 이를 푸리에 계수라고 생각할 수 있고, 그 관계는 다음과 같습니다.

이때 두 푸리에 계수는 켤레복소수(Conjugate Complex Number)입니다. 위의 푸리에 급수를 하나의 항으로 표현할 수 있는데, 이는 다음과 같습니다.

즉, 단 하나의 복소지수함수를 기저해로 갖고, 푸리에 계수 $c_k$의 가중치를 반영한 선형 조합의 형태로 표현할 수 있음을 뜻합니다. 두 푸리에 급수의 형태는 상이해보이지만, 어떠한 표현 기법을 기준으로 했냐의 차이일 뿐 식이 같는 의미는 동일합니다.

2. 복소지수함수를 포함한 푸리에 계수의 결정 (Determinant of Fourier Coefficient in the form of Complex Number)

우리는 이미 $a_k$와 $b_k$를 구하는 방법을 알고 있으므로, 사칙연산을 통해 $c_k$도 얻어낼 수 있긴 합니다. 다만 해당 방법은 번거롭습니다. 그렇기에 복소 형태의 푸리에 급수로부터 바로 푸리에 계수를 얻는 방법에 대해 살펴보고자 합니다. 실수 형태의 푸리에 계수 결정과 동일하게 내적을 활용하게 되며, 복소지수함수의 직교성을 이용합니다.

1) 복소지수함수의 내적 (Inner Prodcut of Exponential Complex Function) 

기존에는 실수 형태에 대해만 내적을 했기에 내적을 엄밀하게 표현하지는 않았습니다. 하지만 허수를 포함한 내적을 진행할 때에는 켤레 복소수를 이용해서 내적을 진행해야 하며, 그 식은 다음과 같습니다.

이를 이용해서 허수를 포함한 지수함수의 직교성을 살펴보겠습니다.

이때 $n=m$이면 적분 결과가 $T$가 나오는 것은 쉽게 확인할 수 있습니다. 그렇기에 서로 다른 두 지수함수를 내적했을 때의 과정만 같이 살펴보겠습니다.

$n\neq m$이라면 적분을 계속 진행할 수 있습니다.

이때 계산 결과를 알기 위해 오일러 항등식에 $\theta = 2\pi(n-m)$을 대입해볼 수 있습니다.

이때 $n, m$이 서로 다른 정수이므로 코사인은 항상 1로, 사인은 항상 0으로 계산되는 것을 확인할 수 있으므로 , 해당 지수 값은 항상 1입니다. 따라서 내적 결과 0이며, 서로 다른 두 복소지수함수는 직교한다는 것을 알 수 있습니다. 내적의 결과를 요약하겠습니다.

2) 푸리에 계수 $c_k$의 결정

복소지수함수의 직교성을 이용해서 푸리에 계수를 결정하겠습니다. 앞서 이야기했듯, 내적의 목적은 직교성을 활용해 하나의 항을 제외한 나머지 항들은 모두 0이 되도록 하는 것입니다. 내적의 결과는 다음과 같습니다.

이때 $m=k$인 경우를 제외한 모든 내적의 결과가 0이 되기 때문에 시그마 기호가 소거되고, 단 하나의 내적값만 얻을 수 있습니다. 이 결과를 정리하면 푸리에 결과를 얻을 수 있습니다.

이로써 우리는 허수를 포함한 형태로 푸리에 급수를 표현할 수 있게 되었습니다. 그 형태를 다시 한번 요약해보고 마치려고 합니다.