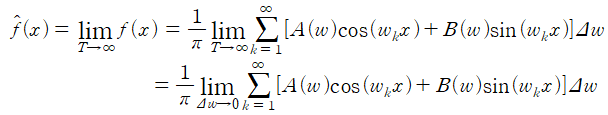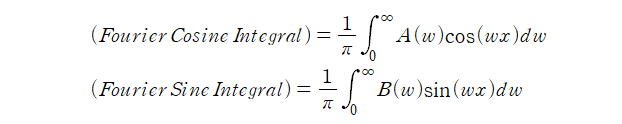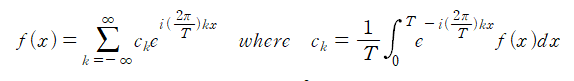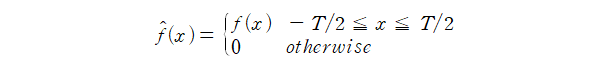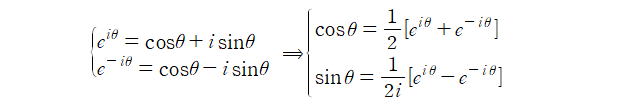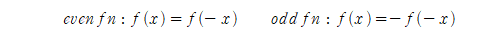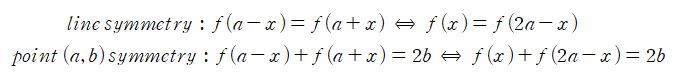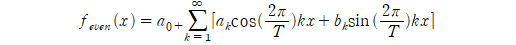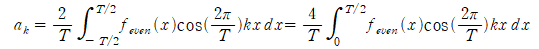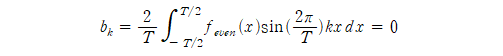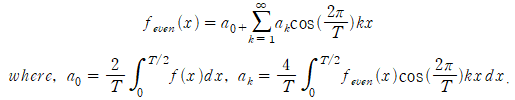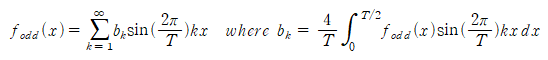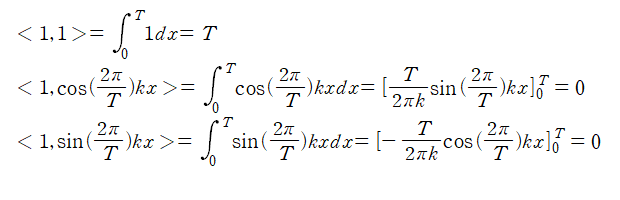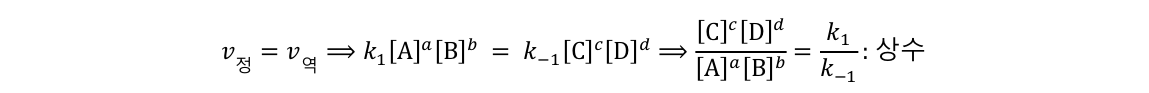화공노트: 화학공학 살펴보기

Contents

1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)

푸리에 변환의 형태와 대칭성이 고려되었을 때의 푸리에 변환을 같이 살펴보겠습니다.

2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)

푸리에 변환이 갖는 몇가지 대수적 특성들에 대해 살펴볼 것입니다.

3. 파르스발 이론 (Parseval's Theorem)

함수와 푸리에 계수 사이의 관계를 설명하는 파르스발 이론에 대해 살펴보고, 이 이론이 가져다주는 의의에 대해 간략하게 살펴볼 것입니다.

1. 푸리에 변환과 푸리에 역변환의 형태 (Form of Fourier Transformation and its Inverse)

1) 푸리에 변환의 의의

푸리에 변환은 주기성을 갖는 함수들에만 적용 가능했던 푸리에 급수의 단점을 극복한 적분 변환 기법입니다. 그 결과 이 변환법은 다양한 분야에서 사용되게 됩니다. 그 중에서도 통신에 대해 공부하는 사람들은 푸리에 변환을 수없이 살펴보게 될 것입니다. 푸리에 변환을 통해 시간 영역에서 정의된 함수를 주파수 영역으로 전사(mapping)하여 여러 해석을 용이하게 돕습니다.

2) 푸리에 변환의 수학적 형태

(1) 푸리에 변환의 관계와 형태

푸리에 변환 $F$에 대해 원함수와 변환된 함수는 아래의 관계를 갖습니다.

어떠한 함수에 푸리에 변환($F$)을 취하면 주파수 함수를 얻을 수 있으며, 반대로 푸리에 역변환($F^{-1}$)을 취하면 원래의 함수를 얻을 수 있습니다.

푸리에 변환과 역변환의 수학적 형태는 다음과 같습니다.

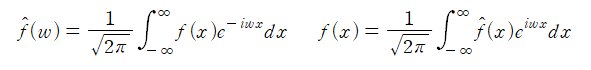
어떠한 함수에 $F$또는 $F^{-1}$를 취했을 때 사용자가 원하는 함수를 얻는 것을 알 수 있습니다.

(2) 대칭성을 갖는 함수에 대한 푸리에 변환

만약 푸리에 변환을 취하려는 함수가 기함수 또는 우함수라면 푸리에 변환을 특수하게 표현하며, 이를 푸리에 사인/코사인 변환(Fourier Sine/Cosine Transformation)이라고 합니다. 만약 원래 함수가 기함수라면 푸리에 사인 변환을, 우함수라면 푸리에 코사인 변환을 취할 수 있습니다. (푸리에 급수와 유사한 것을 알 수 있습니다.) 각 변환의 수학적 형태를 살펴보겠습니다.

푸리에 사인 변환 (Fourier Sine Transformation)

푸리에 코사인 변환 (Fourier Cosine Transformation)

원래의 푸리에 변환과 약간 형태가 상이하여 의문을 가질 수도 있다 생각됩니다만, 결국 똑같습니다. 왜냐하면 대칭성에 의해 적분 구간을 반으로 줄이더라도 적분값을 2배로 하면 그 결과가 같기 때문입니다. (일전에 대칭성을 갖는 함수의 푸리에 급수를 다뤄보며 언급했으므로 참고하시면 될 것 같습니다.)

2. 푸리에 변환의 특성 (Properties of Fourier Trnasformation)

푸리에 변환의 몇가지 특성을 알아보기 위해 한 가지 약속을 하겠습니다. $f(x)$와 $g(x)$는 각각 푸리에 변환을 취할 수 있는 함수이며, 그 관계는 아래와 같습니다.

이 약속을 전제하고 푸리에 변환의 수학적 특성을 설명하겠습니다.

1) 선형성 (Linerarity)

푸리에 변환은 라플라스 변환과 마찬가지로 선형 연산자입니다. 선형성은 가산성(additivity)와 동차성(homogeneity)이 동시에 성립할 때 보장됩니다. 이는 적분 자체가 선형적인 연산자이기 때문인데, 이를 수학적으로 표현하면 다음과 같습니다. 

선형성은 푸리에 변환에 $f(x)$대신 $af(x)+bg(x)$를 대입한 후, $f$와 $g$에 대한 푸리에 변환으로 분리하면 쉽게 얻어낼 수 있습니다. 

2) 도함수에 대한 푸리에 변환 (Fourier Transformation of Derivatives)

n번 미분할 수 있는 어떠한 함수 $f$에 푸리에 변환을 취할 수 있습니다.

이 성질은 수학적 귀납법을 이용해서 증명을 할 수 있습니다. 자세한 증명 과정은 생략하고, 기회가 될 때 다루어보겠습니다.

3) 푸리에 변환의 합성곱 (Convolution of Fourier Transformation)

라플라스 변환에서와 마찬가지로 푸리에 변환에 대한 합성곱(Convolution)을 정의합니다. 형태는 다음과 같ㅅ브니다.

이를 이용했을 때 푸리에 변환된 서로다른 두 함수가 곱해져있을 때, 푸리에 역변환을 취해서 원래의 함수를 얻을 수 있습니다. 

증명 방법은 라플라스 변환의 합성곱과 동일하며, 증명 과정은 따로 자세히 설명하지 않겠습니다.

3. 파르스발 이론 (Parseval's Theorem)

1) 파르스발 이론과 푸리에 급수 (Parseval's Theorem and Fourier Series)

푸리에 급수에 대해 파르스발 이론은 푸리에 급수는 계수들의 정보로 표현될 수 있음을 뜻합니다. 정확히 얘기하자면 주기 함수의 내적(inner product)은 푸리에 계수 사이의 내적과 일정한 관계를 보입니다. 

$f(x)$와 $g(x)$가 동일한 주기를 $T$로 갖는 주기함수라고 하고, 복소지수함수를 포함한 푸리에 급수에서의 푸리에 계수를 각각 $c_k$, $d_k$라고 하겠습니다. 이때, 두 함수 사이의 내적은 푸리에 계수 사이의 내적과 일정한 관계를 갖습니다.

이때 $f(x)=g(x)$인 상황을 생각해보면, 다른 의미를 얻을 수 있습니다. 이 경우 같은 함수의 내적을 통해 얻은 함수의 크기가 결국 계수의 크기와 동일하다는 것을 알 수 있게 됩니다. 식으로는 다음과 같이 표현할 수 있습니다.

2) 파르스발 이론과 푸리에 변환 (parseval's Theorem and Fourier Transformation)

푸리에 변환에서의 파르스발 이론도 결국 동일한 이야기를 합니다. 간단히 설명하고 넘어가겠습니다.

여기까지가 편미분방정식을 본격적으로 시작하기 전에 간략하게나마 다루어본 푸리에 급수와 푸리에 변환 내용입니다. 푸리에 변환에 대한 전반적인 내용이 필요 없더라도 푸리에 급수에서 푸리에 계수 정보를 얻어내기 위해 내적과 직교성을 이용한 방법은 꼭 숙지하셨으면 좋겠습니다. 편미분방정식의 해를 특정하는 데에도 동일한 방법이 사용되기 때문입니다. 복습을 위해 

다음부터는 스트룸-리우빌 정리(Strum-Liouville Theory)와 초기/경계조건(Initial/Boundary Condition)에 대해서 살펴보겠습니다.

Contents

1. 실수형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

- 실수 형태로 표현된 푸리에 급수를 이용해서 푸리에 적분을 표현하는 방법에 대해서 알아볼 것입니다.

2. 복소형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

- 복소지수함수 형태로 표현된 푸리에 급수를 이용해서 푸리에 적분을 표현하는 방법에 대해서 알아볼 것입니다.

 지금까지 우리는 푸리에 급수 공부해왔습니다. 푸리에 급수는 표현하려는 함수가 주기함수여야 한다는 가정 아래 논의되었습니다. 하지만 우리가 다루게 될 많은 함수들은 주기를 갖지 않습니다. 주기도 관찰되지 않으며 해석도 어려운 함수를 다루기 위해서 푸리에 급수를 더 발전시키게 됩니다. 어떠한 주기함수에 대해서 해당 주기를 무한대까지 극한을 보내는 방법을 사용합니다. 즉, 주기의 크기가 무한대에 수렴하는 푸리에 급수를 구하는 것을 뜻합니다. 이를 푸리에 적분(Fourier Integral)이라고 합니다.

푸리에 급수는 실수형태로 정의되거나 허수를 포함한 지수함수의 형태로 표현되었습니다. 그렇기에 각각의 형태로부터 푸리에 적분을 유도하는 과정에 대해 살펴보겠습니다.

1. 실수형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

푸리에 급수로 표현 가능하고 구간 $[-T/2,T/2]$에서 정의된 함수 $f(x)$가 있다고 해보겠습니다. $f(x)$에 대해 푸리에 급수를 작성하겠습니다.

이때 계산상의 편의를 위해 아래의 변수를 정의하겠습니다. 그러면 아래의 관계도 성립하는 것을 알 수 있습니다.

실제로 푸리에 급수가 어떻게 계산되는 지를 파악하기 위해 푸리에 계수를 푸리에 급수에 실제로 대입해보겠습니다. 복잡한 표기를 피하기 위해 위에서 정의한 새로운 변수도 이용하겠습니다.

이제 이 함수의 주기 $T$를 무한대로 보내 하나의 함수로 만들 것입니다. 함수 하나를 정의하겠습니다.

이 함수는 푸리에 급수를 적용할 수 있는 함수의 주기를 무한대로 보내어 주기함수가 아닌 하나의 함수를 정의한 것입니다. 주기를 극한으로 보낼 때 푸리에 급수가 수렴하려면 하나의 가정이 필요합니다. 함수 $f(x)$의 적분결과가 유한하다는 것입니다. 이를 수학적으로 표현할 수 있습니다.

이 가정은 시그마 안에 있는 두 적분항들도 적분이 가능하다는 것을 설명합니다. 이는 삼각함수의 치역때문인데, 아래의 부등식에 표현하겠습니다.

삼각함수의 절댓값은 1보다 클 수 없기 때문에 해당 관계식이 성립하며, 부등식의 삼단 논법에 의해 $f(x)$의 적분 유한성이 확장되어 적용될 수 있습니다. 예시로 코사인함수를 사용했지만, 사인함수의 경우도 결과가 동일하기에, 푸리에계수는 모두 적분이 가능하다는 것을 알 수 있습니다.

적분구간을 고려하여 무한에 가까운 주기를 갖는 함수에 대한 각각의 푸리에 계수를 정의할 수 있습니다.

이 결과들을 종합하여 무한대에 가까운 주기를 갖는 함수에 대한 푸리에 급수를 표현하면 다음과 같습니다.

이때 시그마 기호 안에 묶여있는 삼각함수를 하나의 함수로 본다면 주어진 부분합의 극한을 리만 적분(Rimann Integral)으로 표현할 수 있습니다. (자세한 내용은 미적분학을 참고하면 알 수 있습니다.) 그 결과는 다음과 같습니다.

푸리에 급수를 공부할 때 모든 함수는 우함수와 기함수로 표현될 수 있음을 공부했습니다. 푸리에 적분을 이용해서 함수를 표현해도 이 내용은 동일할 것입니다. 

이때 주어진 함수가 짝수일 때 얻어지는 푸리에 적분을 푸리에 코사인 적분(Fourier Cosine Intergral)이라고 하며, 홀수 함수일 때 얻는 푸리에 적분을 푸리에 사인 적분(Fourier Sine Integral)이라 합니다.

2. 복소형태에 대한 푸리에 적분 (Fourier Integral with Real Form)

본격적인 적분에 앞서 복소지수함수형태를 포함한 푸리에 급수의 형태를 다시 한번 살펴보겠습니다.

함수의 주기를 확장하기 위해 새롭게 함수를 정의하고, 이에 대해 푸리에 급수를 다시 작성할 수 있습니다.

실수형태에서의 푸리에 적분을 구하는 것과 마찬가지로 푸리에 계수를 급수식에 대입한 후 식을 전개하겠습니다.

마찬가지로 몇가지 변수를 새로이 정의하고, 이를 이용해서 다시 함수를 표현하겠습니다.

논의를 위해 함수 $f(x)$가 적분 가능하다고 하겠습니다. (구체적인 설명은 실수로 표현된 푸리에 적분을 참고하시면 되겠습니다.) 편한 표기를 위해 푸리에 계수를 정의하겠습니다.

이 형태는 추후 알게되겠지만 푸리에 변환(Fourier Transformation)의 형태입니다. 이를 이용해서 푸리에 적분을 마저 얻어내겠습니다. 

Contents

1. 실수 형태의 푸리에 급수에서 복소 형태로의 전환 (Transformation from Real Form to Complex Form)

- 오일러 항등식(Euler's Identity)을 이용해서 실수 형태로 표현된 푸리에 급수를 복소수를 포함한 형태로 전환하는 과정에 대해 살펴보겠습니다.

2. 복소지수함수를 포함한 푸리에 계수의 결정 (Determinant of Fourier Coefficient in the form of Complex Number)

- 오일러 항등식을 이용하면 자연상수를 포함한 형태로 푸리에 급수가 표현됩니다. 이때 표현되는 푸리에 계수를 내적(Inner Product)를 이용해서 구하는 방법에 대해 살펴볼 것입니다. 실수 형태의 푸리에 급수와 동일하게 직교성을 활용하여 구하는 것을 확인할 수 있을 것입니다.

1. 실수 형태의 푸리에 급수에서 복소 형태로의 전환 (Transformation from Real Form to Complex Form)

물리학을 다룰 때, 복소수를 차용해서 수식을 표현하는 경우가 많이 있습니다. 오일러 항등식(Euler's Identity)은 실수와 복소수 사이의 관계를 표현하는 대표적인, 그리고 가장 유명한 항등식입니다. 이 수식은 다음과 같습니다.

푸리에 급수를 다시 한 번 살펴보겠습니다. 

푸리에 급수는 삼각함수의 조합을 통해서 어떠한 함수를 비슷하고, 계산에 용이하게 바꾸어 표현하기 위해 정의되었습니다. 그렇기에 그 식은 코사인 함수와 사인 함수를 포함합니다. 오일러 항등식을 변형해서 코사인 및 사인 함수를 자연상수를 이용해서 표현한다면 실수 형태로 정의된 푸리에 급수를 허수를 포함한 형태로 바꾸어 표현할 수 있게 될 것입니다.

$\theta$에 $-\theta$를 대입하면 오일러 항등식의 파생 형태를 얻을 수 있으며, 이를 이용하면 코사인과 사인에 대한 식을 얻어낼 수 있습니다. 약간의 연립방정식만 풀이하면 되므로 중간 계산 과정은 생략하겠습니다. 새롭게 얻은 관계를 표현하면 아래와 같습니다.

이를 이용해서 푸리에 급수에서 사용된 삼각함수를 자연상수의 형태로 먼저 변환하겠습니다. 결과는 다음과 같습니다.

위의 관계를 이용해서 실수 형태의 푸리에 급수의 변환을 시작하겠습니다.

 동일한 지수함수 형태끼리 식을 묶어주어 정리할 수 있습니다.

편한 표기를 위해서 지수함수 앞의 계수를 $c_k$로 정의하겠습니다. 이를 푸리에 계수라고 생각할 수 있고, 그 관계는 다음과 같습니다.

이때 두 푸리에 계수는 켤레복소수(Conjugate Complex Number)입니다. 위의 푸리에 급수를 하나의 항으로 표현할 수 있는데, 이는 다음과 같습니다.

즉, 단 하나의 복소지수함수를 기저해로 갖고, 푸리에 계수 $c_k$의 가중치를 반영한 선형 조합의 형태로 표현할 수 있음을 뜻합니다. 두 푸리에 급수의 형태는 상이해보이지만, 어떠한 표현 기법을 기준으로 했냐의 차이일 뿐 식이 같는 의미는 동일합니다.

2. 복소지수함수를 포함한 푸리에 계수의 결정 (Determinant of Fourier Coefficient in the form of Complex Number)

우리는 이미 $a_k$와 $b_k$를 구하는 방법을 알고 있으므로, 사칙연산을 통해 $c_k$도 얻어낼 수 있긴 합니다. 다만 해당 방법은 번거롭습니다. 그렇기에 복소 형태의 푸리에 급수로부터 바로 푸리에 계수를 얻는 방법에 대해 살펴보고자 합니다. 실수 형태의 푸리에 계수 결정과 동일하게 내적을 활용하게 되며, 복소지수함수의 직교성을 이용합니다.

1) 복소지수함수의 내적 (Inner Prodcut of Exponential Complex Function) 

기존에는 실수 형태에 대해만 내적을 했기에 내적을 엄밀하게 표현하지는 않았습니다. 하지만 허수를 포함한 내적을 진행할 때에는 켤레 복소수를 이용해서 내적을 진행해야 하며, 그 식은 다음과 같습니다.

이를 이용해서 허수를 포함한 지수함수의 직교성을 살펴보겠습니다.

이때 $n=m$이면 적분 결과가 $T$가 나오는 것은 쉽게 확인할 수 있습니다. 그렇기에 서로 다른 두 지수함수를 내적했을 때의 과정만 같이 살펴보겠습니다.

$n\neq m$이라면 적분을 계속 진행할 수 있습니다.

이때 계산 결과를 알기 위해 오일러 항등식에 $\theta = 2\pi(n-m)$을 대입해볼 수 있습니다.

이때 $n, m$이 서로 다른 정수이므로 코사인은 항상 1로, 사인은 항상 0으로 계산되는 것을 확인할 수 있으므로 , 해당 지수 값은 항상 1입니다. 따라서 내적 결과 0이며, 서로 다른 두 복소지수함수는 직교한다는 것을 알 수 있습니다. 내적의 결과를 요약하겠습니다.

2) 푸리에 계수 $c_k$의 결정

복소지수함수의 직교성을 이용해서 푸리에 계수를 결정하겠습니다. 앞서 이야기했듯, 내적의 목적은 직교성을 활용해 하나의 항을 제외한 나머지 항들은 모두 0이 되도록 하는 것입니다. 내적의 결과는 다음과 같습니다.

이때 $m=k$인 경우를 제외한 모든 내적의 결과가 0이 되기 때문에 시그마 기호가 소거되고, 단 하나의 내적값만 얻을 수 있습니다. 이 결과를 정리하면 푸리에 결과를 얻을 수 있습니다.

이로써 우리는 허수를 포함한 형태로 푸리에 급수를 표현할 수 있게 되었습니다. 그 형태를 다시 한번 요약해보고 마치려고 합니다.

Contents

1. 대칭성을 갖는 함수 (Functions with Symmetry)

- 우함수, 기함수 등 대칭성을 갖는 함수를 살펴보겠습니다.

2. 대칭성을 갖는 함수의 푸리에 급수 (Fourier Series and Symmetry Function)

- 대칭성을 갖는 함수를 푸리에 급수로 어떻게 표현할 수 있는지 살펴보겠습니다.

3. 반구간 확장 (Half Range Expansion)

- 일정 구간에서 주기를 갖지 않는 함수를 푸리에 급수로 표현할 수 있습니다. 이는 주어진 구간에서의 함수를 주기를 갖는 우함수/기함수라고 가정을 함으로써 얻어낼 수 있는데, 이 방법에 대해 살펴보겠습니다.

1. 대칭성을 갖는 함수 (Functions with Symmetry)

1) 우함수와 기함수 (Even and Odd Function)

고등학교 시절에 수학과목을 공부하며, 우함수와 기함수를 배워볼 기회가 있었습니다. 간단하게 복습해보겠습니다.

$x$ 대신 $-x$를 대입했을 때의 함숫값을 원래 함수와 비교할 수 있습니다. 이때 함숫값이 같다면, 이를 우함수(짝함수, even function)라고 합니다. 반대로 부호가 반대로 나온다면 이 함수를 기함수(홀함수, odd function)라고 합니다. 우함수는 $y$축에 대하여 대칭인 선대칭 함수의 한 종류이고, 기함수는 원점에 대해 대칭인 점대칭 함수의 한 종류입니다.

2) 선대칭과 점대칭 함수 (Line Symmetry and Point Symmetry Function)

우함수와 기함수를 확장할 수 있습니다. 즉, 어떤 임의의 선에 대한 함수가 있을 수 있고, 비슷하게 어떤 임의의 점에 대해 대칭인 함수도 얻을 수 있습니다. 이를 수학적으로 표현할 수 있습니다.

3) 함수 속에 숨겨진 대칭성 (Symmetry within arbitary function)

어떤 임의의 함수는 우함수와 기함수의 합으로 이루어져 있습니다. 그 이유는 다음과 같습니다.

어떤 함수를 우함수와 짝함수의 관계에 있는 함수들의 합으로 표현해도 그 결과가 동일합니다. 이를 이용해서 푸리에 급수를 대칭을 갖는 함수의 관점에서 살펴볼 수 있습니다.

2. 대칭성을 갖는 함수의 푸리에 급수 (Fourier Series and Symmetry Function)

이제 대칭성을 보이는 함수의 푸리에 급수를 살펴보겠습니다.

1) $[-\frac{T}{2},\frac{T}{2}]$에서 정의된 우함수의 푸리에 급수

푸리의 급수로부터 시작할 수 있습니다.

이때, 푸리에 계수를 결정하여 실제 우함수의 푸리에 급수를 얻을 수 있습니다. 각각의 계수를 구해보겠습니다. 이때 우함수/기함수에 대한 적분의 성질이 사용됩니다. 고등과정에서 배웠을 것이라고 생각하고, 바로 시작하겠습니다.

(1) $a_0$ 구하기

주어진 함수가 y축 대칭이므로, 주어진 구간에서의 적분은 0부터 시작하는 적분의 2배를 취한 것과 같음을 알 수 있습니다.

(2) $a_k$ 구하기

$a_0$를 구하는 것과 동일하게 $a_k$를 결정할 수 있습니다.

주어진 함수와 코사인함수 모두 우함수이므로, 이를 곱한 함수도 우함수입니다. 그렇기에 주어진 구간에 대한 적분을 0부터 시작하는 적분의 2배로 계산할 수 있습니다.

(3) $b_k$구하기

$b_k$도 함수의 대칭성을 이용한 적분의 계산을 이용하면 쉽게 구할 수 있습니다.

우함수와 기함수를 곱하면 기함수가 됩니다. 기함수에 대해서 대칭인 적분 구간에 대해 적분을 진행하면 적분 결과가 0인 것을 알고 있을 것입니다. 그러므로 $b_k = 0$입니다.

(1) ~ (3)을 통해서 우함수(짝수함수)에 대한 푸리에 급수를 얻을 수 있었고, 이를 정리하면 아래와 같습니다. 이처럼 얻는 푸리에 급수를 푸리에 코사인 급수 (Fourier Cosine Series)라고 합니다.

2) $[-\frac{T}{2},\frac{T}{2}]$에서 정의된 기함수의 푸리에 급수

우함수에서 했던 방법을 동일하게 따랐을 때, 대칭인 적분구간에서 정의된 기함수에 대한 푸리에 급수도 얻을 수 있습니다. 부가적인 설명을 생략하고 바로 푸리에 계수를 계산하겠습니다. 그 결과는 아래와 같습니다.

얻어진 푸리에 계수를 바탕으로 기함수(홀수함수)에 대한 푸리에 급수를 얻을 수 있고, 이를 아래에 정리해두었습니다.

우리는 이를 푸리에 사인 급수 (Fourier Sine Series)라고 합니다.

3) 확장 : 제시된 함수를 푸리에 사인/코사인 급수를 이용해서 표현하기

앞서 모든 함수는 원점대칭인 함수와 y축 대칭인 함수의 합으로 구성되어 있음을 이야기 했습니다. 이 성질을 이용하면 주어진 함수의 푸리에 급수를 더 쉽게 구할 수 있습니다.

Step 1 주어진 함수를 원점대칭인 함수와  y축 대칭인 함수로 분리한다.

Step 2 원점대칭 함수에 대한 푸리에 사인 급수를, y축 대칭인 함수에 대한 푸리에 사인 급수를 구한다.

이때 푸리에 사인 급수와 코사인 급수에서 시그마의 index를 다르게 표현했는데, 이 둘을 합쳤을 때 혹시 결과가 다르게 나타날 수 있음을 예방한 것입니다. 같은 함수를 다른 과정을 거쳐 푸리에 급수로 표현하더라도 형태는 같아야 하기에 큰 문제는 없을 것이라고 생각됩니다. 하지만, 시그마를 여러개 사용할 때 함부로 index number를 같게 표현하는 것을 조심해야 함을 강조하고 싶었습니다. 일단, $l, k$를 교차해서 사용하더라도 큰 문제가 없다고 생각하겠습니다.

Step 3 푸리에 사인 급수와 푸리에 코사인 더하여 원래 함수의 푸리에 급수를 구한다.

푸리에 계수를 계산할 때 원래 함수가 아닌 우리가 분리한 우함수/기함수를 기준으로 해야 함을 주의해야 합니다.

이러한 의문이 들 수 있습니다. 그냥 바로 푸리에 급수를 구해도 무방할텐데, 왜 우리는 대칭성을 이용한 절차를 거쳐야 하는가? 이는 푸리에 급수를 구함에 있어 더 편함을 보장하기 위함입니다. 예를 들어 주어진 함수가 $f(x)=x+1$이라면 $y=x$에 대한 푸리에 사인 급수를 구하고 $ y=x$에 대해 푸리에 코사인 급수를 구해서 더하는 것이 바로 푸리에 급수를 구하는 것보다 더 편할 것입이다.

3. 반구간 확장 (Half Range Expansion)

푸리에 사인/코사인 급수를 이용하면, 주기성을 갖고 있지 않은 함수이더라도 푸리에 급수를 구할 수 있게됩니다. 이처럼, 반구간($[0,a]$)에 대해 정의된 함수에 주기성/대칭성 등을 고려하여 푸리에 급수를 구하는 것을 반구간 확장(Half Range Expansion)이라고 합니다. 

대략적인 반구간 확장의 알고리즘은 다음과 같습니다.

Step 1 주어진 함수를 우함수/기함수가 되도록 확장합니다. 

Step 2 해당 우함수/기함수가 일정 주기를 갖고 반복된다고 가정합니다. 그리고 이에 대한 푸리에 급수를 얻습니다.

반구간 $[0,T]$에서 정의된 어떠한 함수$f(x)$를 우함수 및 기함수로 확장하는 반구간 확장을 보여드리고자합니다.

1) 우함수를 이용한 반구간 확장 (Half Range Expansion with Even Function)

Step 1 주어진 함수를 우함수가 되도록 확장합니다. 이를 위해서 반대편 반구간 $[-T,0]$에 새롭게 함수를 정의해야 하고, 이는 수학적으로 다음과 같이 표현할 수 있을 것입니다.

즉, $h(x)$는 원래 반구간에서 정의된 함수 $f(x)$를  y축 대칭하여 확장한 함수입니다.

Step 2 새롭게 얻은 함수 $h(x)$는 $2T$의 주기를 갖는 주기함수라고 가정하겠습니다. (그래야 y축 대칭인 성질을 그대로 이용할 수 있기 때문입니다.) 우함수에 대해 푸리에 급수를 구하는 것이기에 푸리에 코사인 급수를 구하면 될 것입니다.

결국 확장된 함수에서 원래 정의된 구간에 대해 함수를 얻으면 주기가 있다고 생각하고 얻은 푸리에 급수와 그 결과가 동일하게 나타나는 것을 알 수 있습니다.

2) 기함수를 이용한 반구간 확장 (Half Range Expansion with Odd Function)

우함수를 이용했던 것과 동일한 과정을 거치면 반구간확장을 할 수 있습니다. 간단하게 살펴보겠습니다.

Step 1 주어진 함수를 기함수가 되도록 확장합니다. 이는 반대편 반구간에 원점대칭한 함수를 확장한 형태일 것입니다.

Step 2 $g(x)$의 주기가 $2T$라고 했을 때, 이 함수는 원점대칭이므로 푸리에 사인 급수를 얻을 수 있습니다.

Contents

1. 푸리에 급수의 형태 (Formula of Fourier Series)

- 주기를 갖는 함수를 푸리에 급수를 이용해서 어떻게 표현하는지 정의합니다.

2. 푸리에 계수의 결정 (Determinant of Fourier Coefficient's)

- 푸리에 급수를 특정하기 위해서는 푸리에 급수에 포함된 삼각함수의 계수를 결정해야 합니다. 삼각함수 내적의 직교성(Orthogonality)을 이용해서 푸리에 급수의 계수(Fourier Coefficients)를 어떻게 결정하는지 알아보겠습니다. 

3. 푸리에 급수의 수렴성과 급수의 합 (Convergence and Sums of Fourier Series)

- 푸리에 급수의 수렴에 대해 간단하게 살펴보고, 실제 물리적인 의미에서 푸리에 급수어 어떻게 다루어지는지에 대해 살펴보겠습니다.

1. 푸리에 급수의 형태 (Formula of Fourier Series)

1) 푸리에 급수의 정의

표현하고자 하는 함수 $f(x)$가 부분적으로 연속(piece-wise continous)이고, 주기가 $T$인 주기함수라고 가정하겠습니다. 이때 $f(x)$를 삼각함수를 계수와의 조합으로 표현할 수 있습니다.

이때 $\{{a_k\}}'s$, $\{{b_k\}}'s$는 푸리에 계수(Fourier Coefficients)라고 합니다. 푸리에 계수는 삼각함수의 내적의 직교성을 통해 얻어질 수 있는데, 그 결과는 곧 살펴보겠습니다.

이처럼 주기함수 $f(x)$는 $cos(\frac{2pi}{T})kx$와 $sin(\frac{2pi}{T})kx$를 기저해로 하는 선형조합으로 표현할 수 있는데, 이를 푸리에 급수(Fourier series)라고 정의합니다.

2) 불연속지점에서의 푸리에 급수의 표현

푸리에 급수는 부분적으로 연속인 함수에 대해서 표현할 수 있다고 언급했습니다. 정의의 형태를 보면, 삼각함수들의 합으로 표현된 것을 알 수 있으며, 이는 함수 $f(x)$가 전 구간에서 연속이 될 수 있음을 의미합니다. 그렇기에 푸리에 급수는 원래 함수의 불연속부분을 어떻게 처리하는 지에 대해서 살펴볼 필요가 있습니다.

불연속지점에서의 푸리에 급수의 값은 해당 지점에서의 좌극한값과 우극한값의 평균을 갖습니다. 이를 수학적으로 표현할 수 있습니다.

2. 푸리에 계수의 결정 (Determinant of Fourier Coefficient's)

1) 내적으로 표현한 삼각함수의 직교성 (Orthogonality of Trigonometric Function with Inner Product)

푸리에 급수로 주어진 함수를 정의했을 때, 실제 정의한 급수가 실제 함수를 표현하기 위해서는 푸리에 계수를 결정해야 합니다. 이를 위해서는 삼각함수가 직교성(Orthogonality)를 따른다는 것을 이용해야 합니다. 어떤 함수의 직교성은 내적(inner product)을 이용해서 얻을 수 있습니다.  함수의 내적(inner product)을 수학적으로 다음과 같이 표현합니다.

이를 이용해서 삼각함수를 이용한 내적의 결과를 구할 수 있습니다. ($k$는 정수)

한편, 우리가 얻으려는 삼각함수의 직교성은 서로 다른 두 삼각함수를 한 주기 내에서 내적을 취했을 때 그 결과가 0임을 의미합니다. 이를 위해 삼각함수끼리의 내적의 결과를 확인해야 합니다. 계산 과정에서 삼각함수의 항등성을 사용하게 되는데, 해당 개념을 모르겠으면 아래의 글을 살펴보는 것을 추천드립니다.

(1) cos-cos, sin-sin 사이에서의 직교성

우선 코사인 함수끼리의 내적의 결과부터 살펴보겠습니다. ($m$, $n$은 정수)

$m=n$이라면 이는 서로 같은 두 코사인함수를 내적한 것이고, 그렇지않다면  서로 다른 두 코사인함수를 내적하는 것입니다. 이에 따라 적분값은 결과가 다르게 나타납니다.

$m\neq n$이라면 $m-n$또한 하나의 정수이므로 그 적분 값이 0이 될 것입니다.

하지만 $m=n$이라면 서로 같은 삼각함수를 내적하는 것이므로 특정 값을 얻을 수 있을 것입니다.

이를 정리하면 아래와 같습니다.

즉, 서로 다른 두 코사인 함수를 내적하면 그 결과가 0이고, 이는 서로 다른 두 코사인 함수는 서로 직교한다는 것을 의미합니다. 

비슷한 과정을 거쳐 사인 함수 사이에서의 내적도 계산을 해볼 수 있으며, 그 결과 서로 다른 사인함수 사이에서의 직교성도 얻을 수 있습니다.

(2) sin-cos 사이에서의 직교성

마지막으로 사인함수와 코사인함수 사이의 직교성을 살펴보겠습니다.

사인 함수의 경우 전체 주기에 대해 적분을 하면 그 결과는 항상 0이기 때문에 $m$과 $n$의 관계와 무관합니다. 즉, 서로다른 사인, 코사인 함수는 직교성을 갖는 것을 알 수 있습니다.

(1)과 (2)의 결과를 통해 우리는 서로 다른 sin, cos함수를 내적하면 결과가 0이고, 이는 두 함수는 서로 직교한다는 것을 알 수 있습니다. 이 결과를 이용해서 푸리에 계수를 결정해보겠습니다.

2) 푸리에 계수의 결정 (Determinant of Fourier's Coefficient's)

푸리에 급수를 다시 살펴보겠습니다.

계수를 결정한다는 것은 $a_0$, 자연수 $k$에 대한 ${\{a_k \}}'s$, ${\{b_k\}}'s$를 결정해야 함을 의미합니다. 그리고 이 과정에서 위에서 구한 삼각함수에 대한 내적의 결과가 필요하므로, 그 결과만 요약해보았습니다.

푸리에 계수를 결정하는 방식은 편미분방정식의 해의 계수를 결정하는 방법과 거의 동일하므로 그 과정을 잘 이해할 필요가 있습니다. 세 번의 결정을 하게 될텐데, 결국 방법은 똑같습니다. 

"목표로 하는 계수를 제외한 나머지 항들이 모두 0이 되도록 내적을 취함"

연산자 관점에서 보면 전체 함수 중 원하는 대상만을 관찰하기 위해서 내적(적분) 연산자를 취하는 행위라고 말할 수 있습니다. (정확하게는 모르겠지만, bra-ket notation과 관점이 비슷하다고 생각됩니다..) 하나씩 살펴보겠습니다.

(1) $a_0$의 결정

우리의 목적은 $a_0$를 구하는 것이므로, 해당 항을 제외한 나머지 모든 항의 내적의 결과가 0이 되도록 적분을 취해야 합니다. 이를 위해서 내적(적분연산자)을 취할 수 있습니다.

그 결과는 아래와 같습니다.

식을 정리해서 $a_0$을 결정할 수 있습니다.

(2) $a_k$의 결정

비슷한 방법으로 $a_k$도 결정할 수 있습니다. 얻고자 하는 계수가 $cos$에 해당합니다. 우리의 목적은 내적을 통해 $cos$앞의 계수를 제외한 모든 항들을 0으로 만드는 것입니다. 이를 위해 주어진 푸리에 급수에 아래의 내적을 취할 수 있습니다.

그 결과는 아래와 같습니다.

2, 3번째 항은 직교성에 의해 내적 결과가 0이고, 첫 번째 항에서 $k=m$이 아닌 모든 항도 마찬가지로 내적의 결과가 0이므로 이를 정리할 수 있다.

(3) $b_k$의 결정

마찬가지로 $b_k$도 결정할 수 있습니다. 구체적인 과정은 생략하고 간략한 결과만 나타내겠습니다.

(1) ~ (3)의 결과를 바탕으로 함수 $f(x)$를 푸리에 급수로 표현할 수 있고, 이를 특정지을 수 있습니다.

3. 푸리에 급수의 수렴성과 급수의 합 (Convergence and Sums of Fourier Series)

1) 푸리에 급수의 수렴성

미적분학을 공부하다 보면 무한급수의 수렴성에 대해 배운적이 있을 것이다. 푸리에 급수도 결국 무한급수이기 때문에 수학적으로 표현하더라도 실제로는 그 결과가 발산하는 경우가 많다. 하지만 푸리에 급수를 정의할 때 급수의 수렴성에 대해 충분히 고민해보지는 않았다.

푸리에 급수로 나타내려는 함수가 부분적으로 연속이라고 하자. 이때 푸리에 급수가 수렴하기 위해서는 아래의 조건이 필요하다.

(1) 연속인 구간에서는 함수가 미분가능하고

(2) 불연속인 지점들에서는 해당 지점에 대해 좌미분계수와 우미분계수가 존재할 때

연속인 구간에서는 함수값으로 수렴하며, 불연속인 지점에서는 좌극한과 우극한의 평균으로 수렴한다고 앞서 소개했다.

2) 실제 세계에서의 푸리에 급수

물리세계에서 무한은 가상의 개념일 분 실제로 무한의 특성을 띠는 것은 없다. 그렇기에 실제 푸리에 급수는 급수가 아닌 부분합으로 표현되어야 한다. 

$N$이 매우 커질수록 원래 함수에 대한 푸리에 급수의 오차는 작아진다. 불연속인 지점에서도 마찬가지로 오차가 존재한다. 이때, 불연속 지점을 연속으로 잇기 위해 삼각함수가 반드시 진동하는 형태를 가져야 하는데, 이를 '깁스 현상(Gibbs Phenomenon)'이라 한다. 깁스 현상도 $N$이 커질수록 그 정도가 작아진다. 

Contents

1. Introduction (도입)

- 푸리에 급수와 푸리에 변환의 개념과 유용성에 대해 간단하게 소개합니다.

2. Properties of Trigonometric Function (삼각함수의 특성)

- 푸리에 급수와 푸리에 변환을 다룰 때 삼각함수를 가장 많이 다루는 삼각함수의 수학적 특성에 대해 간단하게 살펴봅니다.

1. Introduction (도입)

어떤 함수를 분석하기 위해서 근사(approximation)를 취하는 경우가 많습니다. 대표적으로 어떤 함수를 대수적으로 다루려고 할 때 테일러 급수(Taylor's Series)나 매클로린 급수(Maclaurin's Series)를 사용할 수 있습니다. 하지만 이 방법은 분석하려는 함수가 분석구간에서 연속적이여야 합니다. 연속함수이더라도 근사 기준점으로부터 분석지점이 멀어진다면 오차가 커지는 단점을 갖고 있습니다. 이 문제를 해결하기 위해 푸리에 급수(Fourier Series)나 푸리에 변환(Fourier Transformation)을 이용할 수 있습니다.

푸리에 급수/변환을 이용하면, 불연속적인 함수로 시작하더라도 부분적으로 연속인 함수(piecewise-continuous fucntion)로 바꾸어 표현할 수 있게됩니다. 이는  푸리에 급수/변환이 삼각함수를 기저로 한 조합으로 표현되기에 가능합니다. 변환하려는 함수가 주기함수라면 푸리에 급수를 이용할 수 있습니다. 주기 함수가 아니라면, 주기를 무한대로 갖는 함수로 생각해서 푸리에 적분을 취할 수 있고, 이를 푸리에 변환이라고 합니다. 추후 자세히 살펴보겠습니다.

결국 푸리에 급수와 푸리에 변환을 다룰 때 삼각함수에 대해 잘 알아두어야 합니다. 그렇기에 삼각함수의 몇가지 특성에 대해 알아보고자 합니다.

2. Properties of Trigonometric Function (삼각함수의 특성)

1) 삼각함수는 주기함수입니다. 어떠한 함수가 주기를 $T$로 가질 때 주기함수는 아래와 같이 정의됩니다. 

주기함수에서의 주기는 위의 식을 만족시키는 가장 작은 양수를 의미합니다.

2) 삼각함수는 몇가지 항등성을 갖습니다. (Trigonometric Identity)

(1) 삼각함수의 덧셈정리 (Angle Sum Identitiy)

삼각함수의 덧셈정리는 여러 방법을 이용해서 증명할 수 있지만, 이미 고등수학에서 그 방법이 제시되어 있기 때문에 생략하겠습니다. 삼각함수의 덧셈정리의 결과를 이용하면 삼각함수를 이용한 여러 항등식을 얻을 수 있습니다.

(2) 합에서 곱으로의 표현 (From Sum to Multiplication)

(3) 곱에서 합으로의 관계 (From Multiplication to Sum)

물리적 물성(property)은 시공간의 영향을 받는다. 공간 또는 시간이 변함에 따라 물성도 변화한다. 대표적으로 온도, 에너지 등이 있다. 이러한 물성들은 다변수 함수로 표현된다. 

편미분방정식(Partial Differential Equation)은 물리, 공학에서 주로 사용되는 수학적 도구다. 이는 관찰하고자 하는 물성의 편도함수(partial derivatives)사이의 관계를 나타낸다. 아래는 수직선상의 움직임과 시간의 변화를 고려한 1D equation이다.

$\frac{{\partial}^2 u}{{\partial}^2 t}=c^2 \frac{{\partial}^2 u}{{\partial}^2 x}$

편미분방정식의 해는 시공간에서의 물성의 분포(distribution)를 표현한다. 변수의 변화에 따라 달라지는 물성을 표현하기 때문이다. 그렇기에 편미분방정식을 얻어내는 것과 이를 풀어내는 것 모두 중요한 문제이다. 하지만 편미분방정식을 풀이하는 것은 어렵다. 한 문제를 풀이 하는 데에도 많은 지면을 필요로 하고, 그렇기에 포기하는 사람이 많은 것 같다. 사실 대학교 학부 수준에서 접하게 되는 편미분방정식은 실제의 편미분방정식의 일부일 뿐이다. 손으로 풀 수 있는 극히 일부의 문제들을 다루는 경우가 태반이다. 그럼에도 불구하고 학부 정규 교육과정을 따라가기 위해서나 시험을 보기 위해서 최소한의 편미방은 직접 풀이할 수 있어야 한다. 

처음으로 편미분방정식을 접하고, 수업 시간에 놓친 내용을 위해서 여러 자료를 찾아보는 경우가 많다. 하지만, 영어에 비해 한글로 된 자료가 많지 않다. 상미분방정식, 수치해석, 선형대수학 등 유명한 수학 과목에 비해서는 한글로된 정보가 극히 드물다. 그래서 먼저 편미방을 공부해본사람으로서 약간의 경험을 나눠보려 한다. 전문적인 내용까지는 다루지 못하더라도, 공학수학이나 수리물리학에서 제시된 내용을 차근차근 설명해보려 한다. 

바로 편미분방정식에 대해서 이야기하고 싶지만, 몇가지 알아야 하는 선수지식들이 있다. 이를 먼저 살펴본 후 본격적으로 편미분방정식에 대한 이야기를 이어가려 한다. 현재 아래의 순서에 맞게 글을 게시할 계획이다.

Contents

1. Presquites (선수지식)

1) Fourier Series and Fourier Transform (푸리에 급수와 푸리에 변환)

- 편미분방정식을 풀이하게 되면 상미분방정식과 비슷하게 기저해의 선형결합을 통해 일반해를 얻는다. 이때 각 기저해가 갖는 계수를 결정할 때 푸리에 급수/변환이 사용된다. 그렇기에 이를 어떻게 계산하는지 살펴보려 한다.

2) Strun-Louville Theory (스트룸-리우빌 이론)

- 스트룸-리우빌 이론은 2차 선형 상미분방정식을 소재로 한다. 편미분방정식을 공부하는데 상미분방정식 개념이 왜 필요한지 의문을 가질 수 있다. 편미분방정식을 손으로 풀이할 때 하나의 편미분방정식을 하나 또는 여러개의 상미분방정식으로 나누어 풀이하는 기법이 사용된다. 특히, 편미분방정식으로부터 여러개의 2계 선형 상미분방정식을 얻는 경우가 많다. 따라서 스트룸-리우빌 이론을 다루어 편미분방정식의 풀이를 돕고자 한다.

3) Initial Conditon(IC) and Boundary Conditon(BC) (경계조건)

- 상미분방정식과 편미분방정식의 큰 차이중 하나가 조건을 중요시한다는 점이다. 상미분방정식의 경우 조건이 특별히 제시되어 있지 않아도 일반해를 얻는 데에서 그쳐도 크게 상관하지 않는다. 하지만 편미분방정식의 해는 조건의 설정 형태에 따라서 우리가 얻게되는 최종 해의 형태가 상이하다. 그렇기에 조건에 대해서 조금 더 심도깊은 논의를 해볼 필요가 있다. 경계조건의 제치화(Homogenization)를 다룰 예정이다.

2. Solving Partial Differential Equation (Solving PDE, 편미분방정식의 풀이)

1) Classification of PDE (편미분방정식의 분류)

- 본격적인 편미분방정식의 내용에 대한 공부에 앞서 편미분방정식의 종류를 먼저 알 수 있어야 한다. 각각의 방정식의 종류에 따라 풀이방식이 상이하기 때문이다. 2차 편미분방정식에 대해 (즉, 최대 미분횟수가 2회인 편미분방정식에 대해) 소개를 할텐데, 이 편미방은 Hyperbolic, Parabolic, Elliptic으로 분류된다. 각각을 어떻게 구분하는 지와 예시를 소개할 것이다.

2) Technique for Solving PDE (1) Seperation of Varibales (편미분방정식 풀이 (1) 변수분리법)

- 편미분방정식의 풀이는 편미분방정식을 상미분방정식으로 바꾸는 데에서 시작하는 경우가 많다. 그 중에서 가장 널리 이용되는 변수분리법(Seperation of Variables)을 이용해서 편미분방정식을 풀이하는 방법에 대해 소개하고자 한다. 

3) Technique for Solving PDE (2) Transformation Method (편미분방정식 풀이 (2) 변환을 이용하는 풀이)

- 편미분방정식을 풀이할 때 라플라스 변환 등을 이용해서 상미분방정식으로 전환한 후 풀이를 이어나가는 경우가 있는데, 이 방법을 소개하고자 한다.

4) Technique for Solving PDE (3) Similarity Method (편미분방정식의 풀이 (3) 상사성 변환)

- 특정 경계조건 하에서는 편미분방정식을 단 하나의 상미분방정식으로 변환해서 풀이를 할 수 있다. 이 방법은 유체역학에서 차원해석에 대해 공부를 할 때 접하는 경우가 많고, 처음 접할 시 이해를 하는데 어려움이 있기에 간단하게 소개해보고자 한다.

예정) Special Functions

- Bessel 방정식, Legendre 방정식 등 물리학에서 주로 사용되는 방정식과 그 풀이과정에 대해 소개하고, 각각의 해가 갖는 특성에 대해 이해해고자 한다. 공학수학보다는 수리물리학에서 주로 다루는 주제이며, 그렇기에 내용이 보다 어려울 수 있다. 다룰 수 있는 기회가 있다면 간단히 내용을 얘기해보려 한다.

이어지는 글들에서는 개념에 대한 소개를 이어가고 필요하다면 문제 풀이 과정을 함께 제시하려 한다. 

우리는 더 나은 자신을 원한다. 그렇기에 우리는 오래전부터 자기계발에 대해 많이 다루었다. 미디어의 발달로 성공한 사람들의 모습을 많이 살펴볼 수 있게 되었다. 이는 누군가에게는 동기부여가 되었다. 그리고 성공과 자신의 결점을 대조하며 자책하는 이들도 많이 늘었다. 많은 사람들의 이야기를 접해보았지만, 결국 '하면 된다'는 이야기를 많이 들을 수 있었다. 하지만, '무엇을' '어떻게' 하면 되는지에 대해서 말해주는 이는 많이 없었다. '베스트 셀프'는 삶을 구성하는 여러 부분에 대해서 스스로 생각하는 최고의 자아에 도달할 수 있도록 돕는다.

이 책은 자신과의 대화를 강조한다. 자신의 현 모습을 가감없이 바라보아 잘하고 있는 것과 못하고 있는 것, 그리고 개선되어야 하는 행동을 찾도록 한다. 이 대화로부터 '최고의 자아와 이를 방해하는 반자아'를 얻어야 한다고 말한다. 모든 삶의 영역으로부터. 이 책은 삶의 전 분야에서 우리가 성장하도록 독려함과 동시에 이를 막는 여러 습관들은 하지 말아야 함을 지적한다. 많은 자기계발서들이 성공을 위한 '전략'들을 주장할 때 오히려 성공을 위해 하지 말아야 하는 지점들을 충분히 상기시켜주는 점에서 이 책은 충분히 매력적이였다. 

성장을 위해 하지 말아야 할 것들을 인지하는 것은 새로운 전략을 더하는 것보다 더 어려운 행위다. 자기가 줄곧 해오던 행동이 사실 우리의 성장을 저해하는 것임을 인정해야 하기 때문이다. 우리는 부족한 부분을 인정하는 것을 참 어려워한다. 자신의 결점을 받아들이기 힘들기 때문이다. 하지만 생각해야 한다. 내 부족한 부분을 인식하는 것이 성장의 시작이다. 

나에게도 스스로를 갉아먹는 반자아가 있다. 감정적으로 업다운이 심한 나는 감정을 우선해서 표현할 때가 종종 있고, 결국 나중에는 후회했다. 이는 내가 원하는 명예를 한 순간에 무너트릴 수 있는 위험한 친구이다. 그렇기에 행동하기 전에 내가 하려는 발언/행동이 나를 망치는 행위는 아닌지 먼저 생각해본 후 이어가야겠다고 결심하게 해주었다. 한편, 이 책을 읽으며 생각보다 괜찮은 나의 모습으 내재되어 있다는 것도 깨닫게 되었다. 그리고 일정 부분에서는 최고의 나를 밖에 드러내고 있다는 것도 알게 되었다. 다만 이러한 모습을 반자아가 일정 부분 가리고 있다는 것도 깨닫게 되었다.

다시 한번 말하지만, 우리가 더 나은 스스로를 원하는 것은 너무 당연한 사실이다. 그렇기에 최고가 되기 위해 해야할 행동과, 하지 말아야 하는 행동을 다시 한번 생각해볼 필요가 있다. 자신과 많은 대화를 나누어보자. 자신의 장점과 단점을 반성해보자. 여기서 개선점을 찾고 실천해보자. 그러면 우리는 더 나은 자신에 다다를 수 있을 것이다.

이 책을 읽고 여러가지 결심들을 하게 되었는데, 공유해보려 한다.

1. 내가 행동을 꺼내기 전, 지금의 행동이 최고의 자아와 연결되었는지, 반자아가 지배하고 있는지를 살펴봐야 한다. 즉, 사건 - 대응 사이에 간극을 '의도적으로' 두어야 한다.

2. 알고 있다는 것과 의식하고 있다는 것은 분명히 다르다. 내가 최고가 되기 위해 해야하는 행동과 하지 말아야 할 행동을 주기적으로 상기하자.

3. 삶에는 전방위적인 반성이 필요하다. 스스로와 대화를 많이 할 수 있도록 해야겠다. 

4. 내일의 내가 오늘의 나보다는 나아졌으면 하는 바람을 항상 가져보자. 주어진 순간에 전념하고 최선을 다하자.

Contents

1. 반응물 및 생성물의 농도 변화

2. 부피 및 압력 변화

3. 온도 변화에 따른 평형 이동

화학 반응은 일정 시간이 지나면 평형에 다다른다. 하지만 평형 상태에 놓인 계에 변화를 주면 변화가 해소되는 방향으로 평형의 위치를 변화한다. 특히 농도, 압력, 온도가 변할 때 화학 평형이 변화한다.

1. 반응물 및 생성물의 농도 변화

평형에 놓여 있는 계에서 물질의 농도가 증가하면, 계는 추가된 물질을 소모하는 방향으로 평형이 이동한다. 반면 물질의 농도가 감소하면, 그 계는 감소된 물질을 다시 보충할 수 있는 방향으로 평형이 이동한다. 농도의 변화는 온도 변화가 수반되지 않기 때문에 평형 상수가 기존의 평형 때와 같은 값을 갖는다 반응물과 생성물의 증감에 따라 나타나는 반응의 경향성이 다르므로, 아래의 표를 통하여 어떻게 변화하는지 살펴보자.

2. 부피 및 압력 변화

부피나 압력에 의한 평형의 이동은 평형 상태에의 계가 기체 물질을 하나 이상 포함하고 있어야 한다. 특정 온도의 평형 상태에서 부피의 변화로 압력이 변화하면, 그 변화를 완화하려는 방향으로 다시 평형이 이동한다. 기체의 분자수는 계의 압력을 결정한다. 그러므로 부피와 압력의 변화는 기체 분자수의 변화로 이어진다. 이때 평형 상태가 어떻게 변화할 지는 반응물과 생성물에 포함되어 있는 기체 물질의 반응 계수의 크기 비교를 통해 알 수 있다. 그러므로 같은 경향의 부피와 압력의 변화는 동일한 변화를 야기하지 못하며, 평형 이동을 파악하려는 반응의 반응 계수를 비교하여 우세한 반응을 결정해야 한다. 반응 전후로 기체 분자의 계수 합이 동일하다면, 부피와 압력의 변화는 평형 변화에 영향을 주지 못한다.

한편 계의 부피를 조작하지 않더라도 반응에 관여하는 물질을 추가로 넣으면 부분압력의 변화로 평형을 변화시킬 수 있다. 이는 곧 반응에 관여하지 않는 기체 물질은 계의 전체 압력에만 영향을 줄 뿐, 부분압력에는 어떠한 영향도 미치지 않아 평형을 변화시킬 수 없다. 아래의 표는 반응 전후 기체의 반응 계수의 합이 다른 경우 변화에 대해 평형이 어떻게 이동하는지 정리한 것이다.

3. 온도 변화에 따른 평형 이동

온도에 의한 평형 상태의 변화를 쉽게 이해하기 위해서 반응에서 출입하는 열을 반응물 혹은 생성물로 생각해보자. 흡열반응은 반응을 위하여 열을 사용하기 때문에 열을 반응물처럼 사용하는 반응으로 생각할 수 있다. 반면 발열반응은 반응 결과로 열을 방출하기 때문에 열을 생성물처럼 생각할 수 있다. 이를 화학식에 반영하면 다음과 같다.

온도가 변하면 그 변화를 완화하려는 방향으로 평형이 이동한다. 해당 반응이 흡열인지 발열인지를 고려하면 제공되거나 빼앗긴 열이 평형을 어떻게 이동시킬 것인지 알 수 있다. 예를 들어 흡열 반응의 평형 상태에 열을 가한 경우 반응물(열)이 가해진 것으로 볼 수 있으므로 이를 소모하고자 정반응이 우세해진다. 한편, 농도나 부분압력의 변화는 평형 상수 값에 영향을 주지 못하나 온도에 의한 변화는 평형 상수에 영향을 미친다. 온도 변화에 의한 평형 이동과 변화한 평형 상수를 정리하여 다음 표와 같이 정리할 수 있다.

Contents

화학평형의 개념

평형상수

1. 화학평형의 개념

가역 반응에서 화학적 평형을 관찰할 수 있다. 평형 상태는 어떤 가역 반응이 시간이 충분히 흐른 후에 더 이상 알짜 농도 변화를 관찰할 수 없는 상태를 의미한다. 그렇다고 반응이 전혀 발생하지 않음을 뜻하지 않는다. 평형 상태에 놓인 계를 분자적 관점에서 살펴보면 정반응과 역반응이 모두 발생하는 중이다. 다만 정반응에 대한 반응 속도와 역반응에 대한 반응 속도가 동일하기 때문에 거시적으로 관찰했을 때 변화를 파악하기 힘든 것이다.

2. 평형상수

① 평형상수의 개념

정반응과 역반응을 모두 단일 단계 반응으로 갖는 일반적인 반응을 살펴보자. 다음은 반응식과 정반응과 역반응의 반응 속도를 초기에 넣어준 물질에 대하여 표현한 것이다.

이 반응이 평형상태에 놓여있다면 양방향으로의 반응속도가 동일하므로, 아래와 같이 식을 정리할 수 있다.

즉, 평형 상태에서 농도 사이의 특정한 비율은 일정한 값을 가지며, 이 값을 평형 상수라고 한다. 평형상수는 2가지 변수에 의하여 수치가 결정된다. 평형상수는 반응이 발생하는 온도에 의존한다. 계의 온도가 변하면 반응하는 정도가 변할 수 있기 때문이다. 평형상수는 또한 반응에 대해 의존한다. 가역 반응이 단일 단계 반응이라고 가정하면 반응의 계수에도 의존할 수 있으며 정반응과 가역 반응의 정도, 평형 상태시의 각 물질의 농도 등 반응의 정보에 의하여 평형 상수 값이 변할 수 있다.

② 기체의 압력으로 표현한 평형 상수 $K_p$

만약 반응물과 생성물이 기체를 포함할 경우에는 몰농도 대신 부분 압력을 사용해서도 평형 상수식을 표현할 수 있다.

몰농도를 사용한 평형상수와 구분하기 위해서 $K_p$로 표기한다. 이상 기체 상태 방정식을 이용하면 압력에 대한 식을 온도와 반응에 대한 몰 변화$\delta n$를 이용해서 표현할 수 있다.

이때 $\delta n = (c+d)-(a+b)$라고 하고 몰 농도를 이용한 평형상수를 대입하면 식을 얻을 수 있다.

실제 수치를 계산할 때 이상 기체 상태방정식의 단위를 따라 를 이용하며 온도는 절대 온도를 사용한다.

③ 활동도와 평형상수의 엄밀한 논의

활동도는 이상적인 혼합물 속에서 표준 농도 1M에 대한 해당 물질의 농도 비이거나, 표준 압력 1atm에 대한 해당 물질의 압력의 비이다. 만약 어떤 물질이 0.01M이라면 활동도는 1M에 대한 비 값인 0.01M/1M=0.01로 표현할 수 있다. 하지만 실제 농도와 활동도가 비슷한 경우는 묽은 용액만 해당한다. 진한 용액의 활동도는 용질 사이의 상호작용으로 녹아 있는 용질의 몰수와 다른 값을 보이며 몰 농도와 활동도가 차이가 날 수 있다. 한편, 고체나 액체는 주어진 물질에 대하여 행동하는 경향성이 거의 비슷하기 때문에 활동도가 1로 표현된다.

활동도를 이용하면 농도나 압력을 사용할 때 보다 평형상수를 정확하게 표현할 수 있다. 활동도를 사용하지 않으면 반응식의 계수에 대해 $a+b=c+d$인 경우를 제외하면 단위가 남는다. 그러나 활동도는 단위가 없기 때문에 구한 값을 대입하여 단위 없는 평형상수를 얻을 수 있다. 또한 평형 상수를 구할 때 액체와 고체를 무시하는 이유도 쉽게 알 수 있다. 반응물과 생성물에 있는 모든 물질의 활동도를 평형 상수를 구할 때 사용하더라도 결국 고체 및 기체의 활동도는 1이기 때문에 무시한 것과 같은 결과값을 얻을 수 있다.

④ 반응지수$Q$와 평형 상수의 비교를 통한 반응의 방향성 파악

두 변수에 의해 결정된 평형 상수의 크기로 반응의 경향성을 알 수 있다. 만약 평형 상수 값이 작다면 생성물의 양이 적은 것을 의미하며 역반응이 활발한 것을 의미한다. 반대로 평형 상수 값이 크다면 생성물의 양이 많으며, 정반응이 활발함을 뜻한다. 그리고 평형 상수의 값이 적당히 중간값을 갖는다면 반응물과 생성물이 비슷한 정도로 남아있음을 뜻한다. 화학 공정 등에서는 평형 상수가 매우 작거나 매우 큰 반응을 선호하며, 이는 얻고자 하는 물질을 더 많이 얻을 수 있기 때문이다.

위의 방법은 평형 상수의 크기만을 이용해서 반응이 전반적으로 어떤 상태에서 평형이 형성되는 지를 알 수 있다. 여기에 반응 지수 를 이용하면 현재 상태에서 반응이 어떻게 진행될 것인지도 알 수 있다. 반응 지수는 평형 상수와 값을 구하는 방법이 동일하지만, 대입하는 값이 평형 상태의 활동도가 아니라 특정 시점에서의 활동도를 대입하면 구할 수 있다. 반응 지수와 평형 상수의 비교는 아래의 세가지 경우로 비교할 수 있다.

ⅰ) $Q<K$인 경우에는 생성물의 농도가 작은 경우다. 평형에 도달하기 위하여 생성물이 더 많이 생성되어야 하므로 반응이 왼쪽에서 오른쪽으로 진행되는 정반응이 우세하다.

ⅱ) $Q=K$인 경우에는 평형 상태에 도달함을 뜻한다.

ⅲ) $Q>K$인 경우에는 생성물의 농도가 큰 경우다. 평형에 도달하기 위하여 생성물이 감소해야 하므로 반응이 오른쪽에서 왼쪽으로 진행되는 역반응이 우세하다.

⑤ 다양한 반응에 대한 평형 상수의 결정

역반응, 동일 반응의 반복(계수의 변화), 반응 메커니즘에서의 평형 상수도 구할 수 있다.

ⅰ) 역반응에서의 평형 상수

평형 상수는 (생성물)/(반응물)꼴로 표현된다. 역반응은 반응물과 생성물의 위치가 바뀌는 것이므로 역반응의 평형 상수는 기존의 반응을 기준으로 (반응물)/(생성물)꼴로 표현된다. 따라서 역반응의 평형 상수는 정반응의 평형 상수에 대해 역수 값을 갖는다.

ⅱ) 계수의 변화와 평형 상수

어떤 반응식의 계수가 배 변했다면 그 반응의 평형 상수는 기존의 평형상수의 제곱을 한 값을 갖는다.

이는 반응의 평형 상태에 존재하는 물질들의 농도는 반응 계수와는 무관하지만, 평형 상수는 계수의 변화로 값이 변할 수 있음을 뜻한다.

ⅲ) 반응 메커니즘의 평형 상수

반응 메커니즘의 평형 상수는 각 단일 단계의 평형 상수를 곱한 값과 같다.