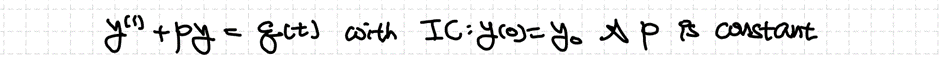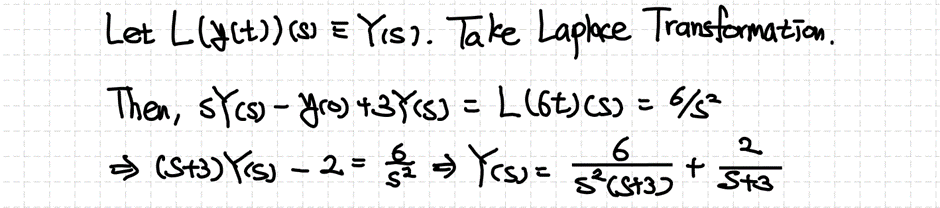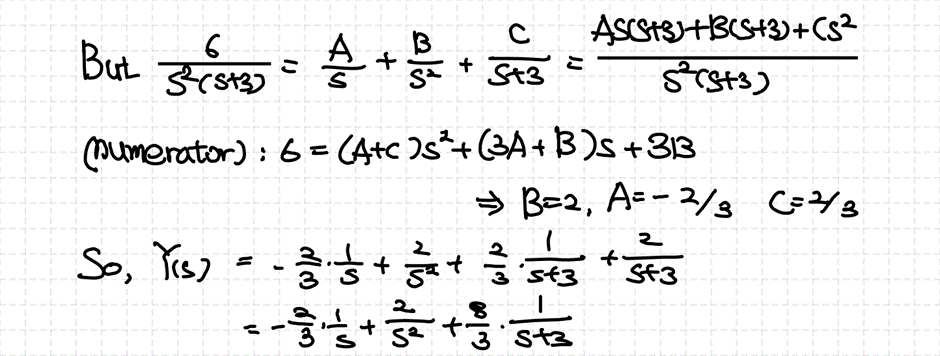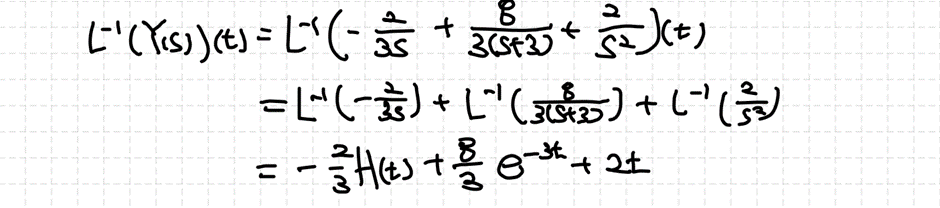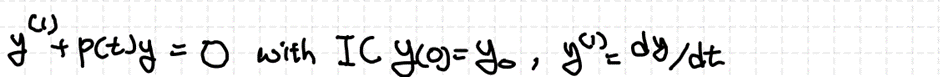화공노트: 화학공학 살펴보기

Contents

1. 2차 선형 상미분방정식의 형태 (the Formulation of 2nd order Linear ODE)

2. 2차 선형 미분방정식의 해의 존재성(Existence)과 유일성(Uniqueness)

3. 2차 상미분방정식의 해의 형태

4. 선형조합과 선형독립 (Linear Combination and Linear Independence)

2차 상미분방정식은 매우 중요합니다. 고전역학에서 속도-가속도 관계를 동시에 표현할 때 2차 선형 상미분방정식 형태를 얻을 수 있습니다. 그리고 많은 편미분방정식을 풀이하기 위해서 2차 상미분방정식을 풀 수 있어야 합니다. 그래서 2차 상미분방정식에 대해서는 조금 자세하게 다룰 필요가 있습니다. 그 중에서도 2차 선형 상미분방정식에 대한 개념을 전반적으로 살펴보도록 하겠습니다.

1. 2차 선형 상미분방정식의 형태 (the Formulation of 2nd order Linear ODE)

2차 선형 상미분방정식의 형태를 상미분방정식의 일반형태로부터 이끌어낼 수 있습니다.

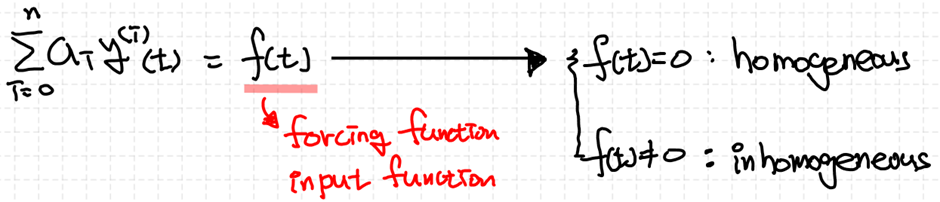
1차 ODE처럼 2차 ODE도 forcing function $r(t)$의 유무에 따라 제차인지 비제차인지 구분됩니다.

2. 2차 선형 미분방정식의 해의 존재성(Existence)과 유일성(Uniqueness)

주어진 미분방정식을 풀이하는 것은 중요합니다. 강의를 들을 때 나오거나 전공서적에 나와있는 문제들은 모두 답이 나오도록 잘 짜여 있습니다. 만약 모델링을 거쳐 미분방정식을 얻어냈을 때, 해당 미분방정식의 해가 존재하는지 그리고 그 해를 유일하게 결정할 수 있는지를 알 필요가 있습니다. 존재성과 유일성은 증명이 가능한 성질이나, 우선 어떤 조건에서 해가 존재하고 또 유일할 수 있는지에 대해 살펴보고자 합니다.

1) 해의 존재성 (Existence)

2차 ODE에서 계수로 취해진 함수 ($p(t), q(t), r(t)$)가 미분방정식이 정의된 구간 $I$에서 연속일 때 해가 존재한다고 생각할 수 있습니다.

2) 해의 유일성 (Uniqueness)

2차 ODE에서 초기조건 $IC$가 다음과 같이 제시되어 있다면 해당 미분방정식은 1개의 유일한 해 (적합해)를 갖습니다.

즉 초기 조건이 2개는 제시되어야 해가 유일하게 결정됩니다. 이는 미분을 하면 정보량이 줄어들고, 반대로 적분을 하면 정보량이 증가하기 때문입니다.

3. 2차 상미분방정식의 해의 형태

1) 제차 상미분방정식의 해의 형태

제차 2차 선형 상미분방정식의 경우 자명한 해를 두어 ODE의 해를 구할 수 있습니다. 자세한 방법은 추후에 살펴보도록 합시다. 그 결과 얻어낸 두 해는 서로 일차독립(linearly independent)이여야 하고, 제차 미분방정식에서의 해는 그 둘의 선형조합(linear combination)으로 결정합니다.

2) 비제차 상미분방정식의 해의 형태

비제차 2차 선형 상미분방정식도 해를 얻을 수 있습니다.

이때 $y_h$는 $r(t)=0$으로 두고 해를 구하는 것입니다. 그리고 $y_p$는 차수비교법, 역연산자법, 그리고 매개변수 변환법을 이용해서 구할 수 있습니다. 마찬가지로 추후에 살펴보도록 하겠습니다.

4. 선형조합과 선형독립 (Linear Combination and Linear Independence)

2차 상미분방정식부터는 해의 기저들을 구하고, 이를 더하는 방식으로 해를 결정합니다. 선형조합, 선형독립, 선형종속에 대해 알아야 합니다.

1) 선형조합 (Linear Combination, Superposition)

선형조합은 기저들을 더하는 것을 얻을 수 있고 수학적으로는 아래처럼 표현합니다.

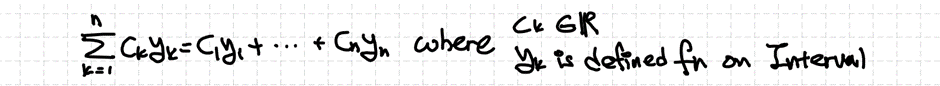
2) 선형독립과 선형종속 (Linear Independence and Linear Dependence)

선형독립과 선형종속은 선형조합에서 사용된 기저해($y_k$)의 일차독립성을 판단하는 것입니다. 만약 선형조합이 0일 때 기저해의 계수들이 어떠한 형태로 나타나는 지에 따라 선형독립인지 아닌지 결정됩니다. 수학적으로는 다음과 같이 표현할 수 있습니다.

이해가 안 될 수 있으니 예시를 통해 설명해드리겠습니다.

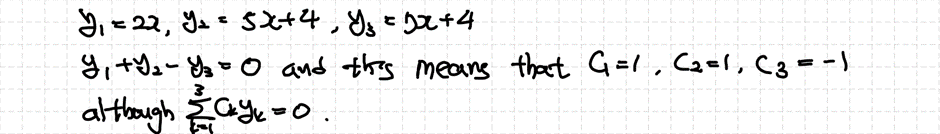
어떠한 3개의 기저해가 있을 때 이를 적당히 더해서 0을 만들 수 있습니다. 즉, 선형조합이 0이 될 때 모든 계수 $c_k$가 0이 되지 않는 조합이 존재하므로 세 함수는 선형종속임을 알 수 있습니다.

선형독립성을 분석해야 하는 함수의 개수가 적으면 적당한 조합으로 그 독립성을 판단하기 쉽습니다. 하지만 해의 형태가 단순한 다항식이 아니거나, 분석해야 하는 함수들의 해수가 너무 많을 때에는 독립성을 판단할 때 실수하기 쉽습니다. 그래서 다른 수학적 도구를 이용해서 선형독립을 판단합니다.

3) 론스키안(Wronskian)

어떠한 구간 $I$에 대해 정의된 $(n-1)$번 미분가능한 해 ${y_1, y_2,⋯,y_n}$에 대해 다음과 같은 수학적 표기를 할 수 있습니다.

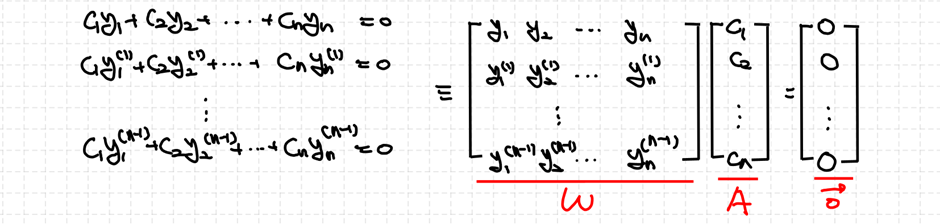
이때 우리가 정의한 행렬 $W$를 론스키안(Wronskian)이라고 합니다.

그리고 행렬 A에 따라서 선형독립과 선형종속이 결정됩니다.

즉, 주어진 해들이 선형종속일 때 론스키안의 Determinant가 0인 것을 결정할 수 있으며, 우리는 명제의 논리를 이용해서 다음의 결과를 얻을 수 있습니다.

즉, $det(W)$이 0이 아니라면 우리는 얻어낸 해를 바로 사용할 수 있음을 의미합니다.

Contents

1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이

2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이

미분방정식 풀이과정을 따르지 않더라도 1차 상미분방정식을 풀이할 수 있습니다. 라플라스 변환을 이용해서 대수식을 정리하고 다시 라플라스 역변환을 이용하면 미분방정식의 해를 구할 수 있습니다.

1. 라플라스 변환을 이용한 제차 1차 선형 상미분방정식의 풀이

예시를 통해서 라플라스 변환을 이용해서 ODE를 풀어내는 방법을 살펴보겠습니다.

EX

우선 각 항에 라플라스 변환을 취해서 식을 대수 영역으로 전환해줍니다.

그 후 라플라스 변환이 취해진 해에 대해 식을 다시 정리할 수 있습니다.

우리가 원하던 해는 대수방정식의 해가 아니라 미분방정식의 해이기 때문에 위의 결과에 라플라스 역변환을 취해줍니다. 그러면 미분방정식의 해를 얻을 수 있습니다.

2. 라플라스 변환을 이용한 비제차 1차 선형 상미분방정식의 풀이

제차 미분방정식을 풀이할 때와 마찬가지로 라플라스 변환을 취하고, 라플라스 변환된 해에 대해 식을 정리할 수 있습니다.

정리된 식의 형태를 살펴보면 homogeneous 일 때의 해($Y_h(s)$)와 특수해($Y_p(s)$)의 조합인 것을 확인할 수 있습니다. 이제 라플라스 역변환을 취하면 미분방정식의 해를 구할 수 있을 것입니다.

이해를 위해 예시를 살펴보겠습니다.

EX

우선 라플라스 변환을 취해서 대수방정식을 얻은 후 식을 정리합니다.

이제 라플라스 역변환을 취해 식을 정리해주어야 하는데, 이를 위해서 식을 재정리할 필요가 있습니다. 보통 라플라스 역변환을 위한 식 정리는 유리식의 항등성을 이용합니다.

라플라스 역변환을 취하면 미분방정식의 해를 얻을 수 있습니다.

여기서 $H(t)$는 Heviside Step Function이고, 주어진 미분방정식을 $t>0$에 대해 고려하면 $H(t)=1$로 두고 미분방정식의 해를 사용하면 됩니다. (사실 $t$가 시간인 경우가 많아 $t>0$에 대해서 고려하긴 합니다.)

Contents

1. 1차 선형 상미분방정식의 형태 (Formula of the first order ODE)

2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)

   - 제차 1차 선형 상미분방정식의 풀이

   - 비제차 1차 선형 상미분방정식의 풀이

1. 1차 선형 상미분방정식의 형태 (Formula of first order ODE)

1차 선형 상미분방정식은 아래의 형태를 갖습니다.

종속변수가 총 미분된 횟수를 미분방정식에서의 차수라고 생각할 수 있습니다. 여기서는 y가 한번 미분되었다는 것을 나타내기 위해 ‘ 대신 (1)을 윗첨자로 사용했습니다. 마찬가지로 forcing function으로 사용된 q(t)가 0이면 이 미분방정식은 homogeneous ODE이며, 0이 아니라면 Inhomogeneous ODE입니다.

2. 1차 선형 상미분방정식의 풀이 (Solving 1st order Linear ODE)

1) 제차 1차 선형 상미분방정식 (Homogeneous 1st order Linear ODE)

초기조건(IC)이 주어진 homogeneous ODE는 다음과 같습니다.

이 문제는 변수분리법(Separating Variables)을 이용해서 비교적 쉽게 해결할 수 있습니다.

변수분리법은 적분하고자 하는 변수들을 한 곳에 몰아 적분을 비교적 편하게 수행하도록 하는 기법입니다. 이 상황에서는 dy 와 dt를 각 항으로 분리해서 식을 다시 작성할 수 있습니다.

왼쪽 항은 적분이 가능하지만 오른쪽 항은 p(t)의 형태에 의존하기에 문제 상황에 맞게 계산해야 합니다.

적분상수는 결국 초기조건에 의해 결정됩니다. 그렇기에 위의 과정을 거쳐 식을 정리할 수 있습니다.

예시 상황을 들어 초기조건을 적용하는 방법을 보여드리고자 합니다.

EX

이때 * 과정을 이해하기 조금 어려울 수 있습니다. 표현만 같은 거지 엄밀하게 따지만 다른 상수이긴 하지만, 결국 초기조건에 의해서 정해지는 값이므로 표현해둔 것입니다. 초기조건을 대입해서 상황에 적합한 해를 얻을 수 있습니다.

2) 비제차 1차 선형 상미분방정식 (Inhomogeneous 1st order Linear ODE)

초기조건(IC)이 주어진 inhomogeneous ODE는 다음과 같습니다.

inhomogeneous ODE는 ODE의 일반형이라고 생각할 수 있습니다. 이 ODE의 해는 적분인자(Integrating Factor)를 이용해서 유도할 수 있습니다. 그 결과는 다음과 같습니다.

여기서 C는 문제 조건에 의해 정해질 것입니다.

다만 이 공식을 적용할 때 유의해야 하는 부분이 있습니다. 1차 미분된 항 앞의 계수가 1임을 반드시 확인해야 합니다. 예시를 통해서 살펴보겠습니다.

주어진 미분방정식의 1차항 계수가 3이기 때문에 이를 1로 만들어야 하고, 이를 위해 3으로 나누어서 다시 ODE를 작성한 것입니다. 이를 위의 식에 넣어서 계산할 수 있습니다.

초기조건을 이용해서 상수 C를 결정할 수 있습니다.

나타나는 해의 형태를 다시 정리했을 때 homogeneous ODE 였을 때의 해에 특수해가 더해진 것임을 다시 한번 확인할 수 있습니다.

Contents

1. 선형 상미분방정식 (Linear ODE)

2. 상미분방정식의 일반해 (General Solution of ODE)

3. 초기조건(Initial Condition, IC)과 경계조건(Boundary Condition, BC)

4. 미분방정식의 해 구하기 (Solving ODE)

미분방정식은 화학공학에서 빼놓을 수 없는 수학적 도구입니다. 아무리 식을 잘 세워놓았더라도 미분방적식을 풀이할 수 없다면 문제 상황에서의 해답을 찾을 수 없습니다. 개념설명과 문제풀이를 바탕으로 미분방정식에 대해 공부해고자 합니다.

1. 선형 상미분방정식 (Linear ODE)

미분방정식에 하나의 변수만 개입되어 있을 때, 우리는 이 미분방정식을 상미분방정식(Ordinary Differential Equation, ODE)라고 합니다. 그 중에서 선형 미분방정식은 다음과 같이 작성할 수 있습니다.

forcing function이 0일 때 우리는 이를 제차상미분방정식(Homogeneous ODE)라고 합니다. 만약 그렇지 않은 경우에는 이 미분방적식을 비제차상미분방정식(Inhomogeneous ODE)라고 합니다.

2. 상미분방정식의 일반해 (General Solution of ODE)

1) 제차상미분방정식의 일반해

제차상미분방정식은 미분방정식으로부터 얻어지는 해들의 선형조합으로 일반해를 얻을 수 있습니다.

2) 비제차상미분방정식의 일반해

비제차상미분방정식은 해당 미분방정식이 제차였을 때 얻어지는 해와 비제차일 때 얻을 수 있는 특수해의 선형조합으로 일반해를 표현합니다.

3. 초기조건(Initial Condition, IC)과 경계조건(Boundary Condition, BC)

우리가 얻는 미분방정식과 그 일반해는 대개 지배방정식(Governing Equation)인 경우가 많습니다. 즉 보편적으로 나타나는 현상들을 설명할 수 있는 수식임을 의미합니다. 하지만 공학에서는 이러한 문제들을 자신의 상황에 맞게 적용해서 결과를 얻어야 합니다. 그래야 해당 문제를 정량적으로 풀어낼 수 있습니다. 그래서 미분방정식의 적합해를 끌어내기 위해서 초기조건 또는 경계조건이 필요합니다. 구체적으로 문제풀이를 시작할 때 자세히 살펴보겠습니다.

4. 미분방정식의 해 구하기

상미분방정식은 2가지 관점에서 해를 구할 수 있습니다  

1) 미분방정식의 해를 직접 구하는 경우

대개 알려져 있는 미분방정식의 경우 문제를 푸는 순서가 정해져 있습니다. 즉 공식 등에 대입해서 문제를 바로 풀이할 수 있습니다.

2) 라플라스 변환을 이용해서 해를 구하는 경우

1)의 방법으로 문제를 풀이하면 적분 연산이 필수적인데, 이는 번거로움을 동반합니다. 그래서 라플라스 변환을 이용해서 미분된 형태의 식을 대수방정식(Algebric Equation, AE)로 변환해서 식을 정리한 후 다시 라플라스 역변환을 통해 해를 구할 수 있습니다.

우선 주어진 미분방정식에 라플라스 변환을 취해줍니다. 그 후 식을 정리해서 라플라스 변환이 취해준 해와 나머지 항들을 분리해서 적어줍니다.

 그 후 라플라스 역변환을 취해서 다시 원래 구해야 하는 해를 얻을 수 있습니다.

문학작품을 볼 때 어떤 생각이 드는가? 나는 문학작품은 공감과 많이 관련되어 있다고 생각하고, 고등학교 때 그렇게 배웠던 것 같다. 주인공에 이입해서 감정상태를 판단하고 사건들을 정리해나가고… 이해되지 않는 부분들이 있었지만 어쨌든 주인공에 이입해서 문학을 대했다.

‘우리는 지금 문학이 필요하다’는 여러분이 갖고 있는 문학에 대한 고정관념을 깬다. 문학이 우리이게 주는 다양한 효과에 대해 설명한다. 문학 작품을 읽고 느꼈던 설명하기 미묘한 감상들이 사실은 작가들의 의도적인 구성이었음을 밝힌다. 그리고 여러분이 특정 효과를 내기 위해 읽을 수 있는 문학 작품들도 소개한다. 단순히 문학을 글로만 바라보지 않고 하나의 ‘테크놀로지’로 다룬다. 즉, 우리가 느끼고 있는 감정적 문제들을 문학 작품을 읽으면서 해소할 수 있다고 이야기하고, 실제로 그 효과들을 자세히 설명한다.

다양한 효과들이 소개되어 있지만, 슬픔은 공감해주는 이들이 있다는 것을 깨달을 때 해소될 수 있다는 부분을 인상 깊게 읽었다. 문학은 이 세상 어딘가 자신과 비슷한 슬픔을 느끼고 있는 사람들이 있음을 일깨워 우울함에서 벗어날 수 있도록 도와준다고 한다. 그리고 문학은 우리를 자극하기 위해 애매모호함을 많이 사용한다고 한다. 이는 대상을 완성하고자 하는 우리의 욕구를 건드리고, 독자가 태도를 의식적으로 바꿀 수 있도록 기능하도록 돕는다.

문학은 허구의 산물이지만, 그 속에는 작가들은 의도한 효과를 주기 위해 노력했던 치열함이 담겨있다. 우리는 문학을 읽으면서 감정을 느낄 뿐 아니라 자신의 상처도 치유할 수 있다. 다양함을 추구해서 나의 존재 이유를 설명할 수도 있다.

문학을 잘 읽지는 않지만, 그럼에도 문학의 존재 이유에 대해 생각해볼 수 있었다. 당분간 문학을 접할 기회는 적겠지만, 문학에 관심 있는 이들에게, 그리고 문학을 너무 단순하게 여기고 있는 이들에게도 추천하고 싶은 책이다.

무의미한 삶 속에서 살아가고 있다는 착각을 하는 사람들이 너무 많다. 스스로 노력하지 않으면서 찬란한 순간이 다가오기 원한다. 심지어 SNS를 보며 대상의 빛나는 점과 자신의 초라한 부분을 대조하며 괴로워하고, 나를 삶의 구렁텅이에서 구해달라 한다. 하지만 빛나는 순간들은 우리의 힘으로 만들 수 있다. 히스 형제의 책 ‘순간의 힘’은 무료한 일상의 고양을 불러일으키는 방법을 알려주어 우리가 보다 긍정적이고 다채로운 삶을 살 수 있도록 도와준다.

내용을 간단히 소개하겠다. 우리는 누군가에게 진실을 직면하게 할 수 있지만, 그의 행동도 변하도록 할 수 없다. 단지 그들이 스스로 깨닫도록 시간을 두고 환경을 마련해주는 것이 필요하다. 실패를 통한 자기 확장은 성장을 위한 필수 요소이다. 누군가를 인정함으로써 그에게 긍지를 선사할 수 있다. 목표를 세부 복표로 분할하여 하나의 이정표를 만들라. 그러면 보다 성취의 순간을 자주 느낄 수 있을 것이다. 난감한 상황을 해결하는 것을 상상해보는 것은 우리가 후에 유사한 문제를 마주했을 때 용기를 보다 쉽게 낼 수 있도록 도와준다.

책의 내용만 놓고 보면 어디선가 들어본 내용들이 많을 것이다. 하지만 이 책은 뻔해 보이는 지혜를 실제로 우리가 실천하고 있는지를 반문하고, 그렇지 않다면 구체적인 방법을 제시하여 우리의 실천을 돕고, 사례를 통해서 우리도 할 수 있다는 용기를 불어넣어준다. 그렇기에 이 책을 읽는 것이 의미가 있는 것이다.

나를 특별하게 만들고 누군가도 특별하게 만들 수 있는 방법을 제시해준 ‘순간의 힘’을 읽게 되어 감사하다. 새로운 것을 시도할 때는 용기가 필요하다. 하지만 나름의 시뮬레이션으로 닥치는 어려움들을 극복하고자 한다. 시간이 흘러 이 글을 다시 읽게 되었을 때 무언가를 다양하게 할 뿐 아니라 나의 삶의 태도가 변해있으면 좋겠다. 지금보다 더 다채로운 나의 모습을 기대하고 싶다.

저자는 학습을 여러 관점에서 정의하는데, 이를 아래처럼 요약할 수 있다.

학습은 주의를 집중하고, 시행착오를 두려워하지 않으며 시도의 결과를 숙달하고 복기하는 행위이며,

우리는 학습에 적극적인 자세로 임해야 한다.

어쩌면 우리는 이미 학습하는 방법을 알고 있었을 지 모른다. 다만 첫걸음을 딛는 것을 두려워하거나, 결과물을 낼 때까지 버티는 것을 힘들어하는 등 여러 핑계를 대며 학습을 외면한 것일지도 모르겠다. 그럴수록 우리 시냅스의 여백은 기존의 것들로 가득 채워진다. 이는 스스로 변화할 수 있는 가능성을 포기하는 것과 마찬가지다. 남아있는 나의 빈 공간을 새로움으로 채우리면 지금 당장 시작해야 한다. 지금 이 순간이 학습을 시작하기 가장 빠른 시기이다.

이 책을 읽으며 학습에 대한 여러 오해도 풀 수 있었다. 그 중에서 아이들의 지식 수준은 백지가 아니며, 일정 수준 이상 선험적으로 완성되어 있다는 것이다. 아이들은 자신이 알고 있는 것과 이해한 바를 명료하게 표현하지 못할 뿐이지 생각보다 많은 것을 알고 있다고 한다. 이 사실은 유년기의 스트레스가 성인이 된 자들을 괴롭게 하는 것을 설명하는 데 도움이 되는 사실이라 생각된다.

그리고 학습에서의 에러에 대해 생각해볼 수 있었다. 우리가 틀릴 수 있는 용기를 지녀야 한다고 종종 이야기를 듣는다. 이는 틀림 그 자체에 대해 부정적 평가 또는 체벌을 받았기 때문이다. 틀림은 학습에서 기본으로 필요로 하는 자세이다. 우리는 결과적 측면에서 자신의 행위가 맞고 틀림을 이야기할 것이 아니다. 답이 나오지 않은 문제 해결을 위해 자신의 가설을 테스트하는 순간에 용기가 필요하다. 결과를 받아드릴 결의가 아니라 나의 현 상황을 직시하겠다는 용기가 필요한 것이다. 가능성이 있는 상태로 나를 내버려 두는 것을 제일 부끄럽게 여겨야 한다.

1. Introduction

결정 구조를 나타내는 모형을 만들어보고 고체의 구조를 이해해 보는 것을 목표로 한다.

2. Chemicals & Apparatus

스티로폼 구 흰색(20mm) 43개, 이쑤시개 3개, 글루건 1개, 글루건 봉 2개, 자

3. Procedure

실험 1 단순 입방 격자 만들기

1) 같은 크기의 20mm 흰 공 3개를 이쑤시개를 사용하여 틈이 업게 붙여서, 정사각형의 형태로 만든다. 같은 2개의 층을 만든다.

2) 1층 위에 2층을 올리고 이쑤시개로 연결한다. 두 층은 정확히 중심이 일치하게 붙인다.

3) 완성된 단순 입방 격자를 촬영하고, 단위 격자를 Data sheet에 그린다.

4) 스티로폼 공을 다시 빼서 다음 과정에 활용한다.

실험 2 체심 입방 격자 만들기

1) 자를 이용하여 20mm 스티로폼 구 3개를 이쑤시개에 직선으로 틈이 없게 끼워, 정육면체의 맞모금(대각선)을 만든다. 이때 흰 공을 사용하고 가운데는 파란색을 사용한다.

2) 만든 맞모금 가운데 구에 이쑤시개를 수직으로 끼워 20mm 흰 공 2개를 틈이 없게 끼워 고정시킨다.

3) 3개를 끼운 정사각형을 사선으로 세워, 나머지 4개의 20mm 흰공을 위와 아래에서 가운데 구에 2개씩 글루건으로 고정한다.

4) 나머지 모든 공을 글루건으로 고정하고, 이쑤시개를 제거한다.

5) 완성된 격자를 촬영하고, 꼭지점의 위치를 표시하여 칼로 잘라 단위 세포를 만든다. 사진을 촬영한 후, 격자 상수, 배위수, 단위 세포 부피와 입자 점유율을 구한다.

실험 3 육방 체밀 격자 만들기 (hcp)

1) 글루건을 이용하여 20mm 스티로폼 흰 구 7개를 육각형모양으로 붙여 1층과 3층 2개를 만든다.

2) 마찬가지로 글루건을 이용하여 20mm 스티리폼 흰 구 6개를 삼각형 모양으로 붙인다.

3) 육각형 모양 1층의 틈 위에 노란 공 삼각형 모양을 2층으로 글루건으로 고정한다.

4) 만들어 놓은 육각형 모양 3층을, 2층의 틈 위에 2층과 동일한 위치로 붙인다.

5) 완성된 육방 최밀 격자를 촬영하고, 꼭지점의 위치를 표시하여 칼로 잘라 6각 기둥의 단위 격자를 만든다.

6) 단위 격자의 사진을 촬영한 후, 격자 상수, 배위수, 단위 세포 부피와 입자 점유울을 구한다.

실험 4 면심 체밀 격자 만들기 (fcp)

1) 20mm 흰 공 6개를 삼각형 모양으로 붙여 2층을 만든다.

2) 또 다른 20mm 흰공 6개를 삼각형 모양으로 붙여 3층도 만들고, 글루건을 이용하여 공으로 만든 2층의 틈 위에 얹어 서로 60도 어긋나게 붙인다.

3) 만든 두 층의 맨 아래와 위의 가운데 틈에 20mm 흰 공을 한 개씩 붙여 1층과 4층을 만든다.

4) 결정 격자를 돌리면서 면심 입방 구조가 되는 방향을 알아본다. 격자를 촬영하고 꼭지점의 위치를 표시하여 칼로 잘라 단위 격자를 만든다.

5) 격자 상수, 배위수, 단위 세포 부피와 입자 점유율을 구한다.

4. Data & Results

1) 결정 격자와 단위 격자

2) 단위격자 안의 총 원자수

3) 배위수 

4) 입자점유율 (스티로폼 구의 반지름 $r_1=22mm$)

5. Discussion

이번 실험을 통해서 이론상으로 생각했던 금속의 결정 격자 구조와 단위 격자 구조를 살펴볼 수 있었다. 단위 격자에 존재하는 원자수와 단위 세포의 부피 사이의 관계를 이용해서 입자 점유율을 구해볼 수 있었다. 단순 입방이 가장 수치가 작게 나타났으며, 그 다음으로는 체심 입방이, 그리고 면심 입방과 육방 최밀 구조가 같은 수치로 가장 높은 입자 점유율을 보였다. 면심 입방 구조와 육방 최밀 구조가 배위수와 입자점유일이 같은 것으로 보아 입방 격자 구조를 갖는 금속 중 가장 조밀하게 쌓은 구조는 면심 입방 구조이며, 육방 격자 구조를 갖는 금속 중 가장 조밀하게 쌓은 구조는 육방 최밀 구조인 것을 생각해볼 수 있다. 한편, 금속 결합 구조를 통해서 여러가지 질문들에 대해서 생각해볼 수 있다.

질문 1 금속 결정이 서로 다른 구조를 가지게 되는 가장 큰 이유와, 특히 어떤 종류의 금속이 체심 입방 구조를 하며, 이 금속들의 특징은 무엇인가?

금속 결정은 각 금속이 갖는 반지름의 크기에 영향을 가장 많이 받는다. 금속들이 조밀하게 쌓이려고 해도 해당 원자의 반지름이 충분히 크다면 기대한 조밀 구조를 쌓을 수 없기 때문이다. 보다 확장하여 이온 결합 결정의 경우, 양이온과 음이온의 비율에 따라서 체심 입방 혹은 면심 입방 구조 등이 결정될 정도로, 결정을 구성하는 원자의 크기가 금속 결정이 다른 구조를 갖게 영향을 미친다.

체심 입방 구조는 단위 세포의 중심에 금속 원자 하나를 온전히 갖고 있다는 것에서 다른 단위 세포들과는 구분이 되는 특징을 가지고 있고, 이에 따라 배위수가 8로 확인된다. 또한 각 꼭짓점 에도 원자가 채워져 있으므로 중심에 배치된 원자도 함께 고려하면 한 단위 세포에 원자 2개가 채워져 있는 것을 알 수 있다. 체심 입방 구조를 갖는 금속들의 종류는 다양하지만 대표적으로 1족 금속에 해당하는 알칼리 금속이 체심 입방 구조를 갖는다. 이는 대부분의 고체들이 최밀 구조를 갖는 것과는 다른 경향성을 갖는다. 이는 다른 금속들에 비해서 단위 격자 사이에 빈 공간을 많이 갖게 되어 다른 금속들과 비교했을 때 밀도가 작은 것을 관찰할 수 있다. 그리고 알칼리 금속은 같은 주기에서 가장 원자 반지름이 크므로 그만큼 결합력이 약해진다. 그래서 같은 구조를 갖는 금속들과도 비교했을 때에도 더 물고 낮은 녹는점을 갖는 것을 알 수 있다. 또한 체심 입방 구조를 갖는 알칼리 금속들의 단면은 광택을 보이는데, 이는 금속 결합에 의해서 관찰되는 자유전자 때문이다. 자유 전자는 가시광선의 대부분을 반사하기 때문이다. 다만, 1족에 속하는 금속들은 반응성이 매우 커서 광택이 나는 단면은 매우 짧은 시간 동안에만 관찰이 가능하다.

질문 2 단순 입방 구조는 자연계에서 발견하기 어렵고, 폴로늄(Po)만이 이 구조를 갖는다. 단순 입방 구조의 안정성이 낮은 이유를 설명하시오.

금속 원자들은 최대한 조밀하게 충진되려고 한다. 같은 종류의 원소로 되어 있기에 원자 반지름이 모두 같을 수 있기 때문이며, 가장 인접한 원자와의 거리가 최소가 되어야 결합에너지를 낮추어 안정해질 수 있기 때문이다. 그리고 조밀하게 쌓여야 금속 원자가 갖는 양이온들을 전자구름이 충분히 가려주어 전기적으로 중성으로 만들어 줄 수 있기 때문이다. 하지만 단순 입방 구조는 각 원자들이 결합에 관여한다고 했을 때 가장 멀리 떨어져 있는 결합 형태를 보인다. 즉, 결합에너지가 낮아지지 못해서, 원자핵 사이의 반발력을 감당할만한 전기적 인력을 형성하기 힘들기 때문에 결합에너지가 최소값을 갖기 않게 되며, 이는 물질이 불안정해 쉽게 붕괴될 수 있음을 설명한다.

질문 3 금속 결합을 설명하는 분자 오비탈 이론에서 결합 오비탈과 반결합 오비탈들이 수평으로 존재하는 것이 아니라 에너지 준위차가 작은 띠로 존재하는 이유를 결정격자구조로 설명하시오.

금속 결합을 설명하는 방법에는 2가지가 있다. 첫 번째로는 전자 바다 모형으로 금속 결합을 설명하는 것인데, 이 이론으로는 금속 결합의 세기가 원자수에 비례해서 증가하다가 다시 감소하는 현상을 보이지 못하기 때문에 분자 오비탈을 이용한 설명이 요구된다. 금속들은 결정 격자에 따라서 매우 규칙적이고 반복적인 구조를 갖게 된다. 이 때문에 분자 오비탈 사이에서 특별한 성질이 관찰된다. 위의 그림을 통해 살펴보도록 하자. 하나의 금속만 존재할 때의 전자배치와 달리, 금속들이 규칙적인 배치를 가지며 결합을 진행하게 되면, 결합 오비탈과 반결합 오비탈 사이의 간격이 점차 줄어드는 것을 확인할 수 있다. 실제 금속은 결정 격자 내에서 무수히 많은 수의 금속이 배치되어 있으며, 이 금속들의 오비탈들을 모두 고려하면 그 간격이 매우 작아서 마치 하나의 띠처럼 오비탈 전자 배치가 형성되는 것을 확인할 수 있다. 이를 보고 고체의 띠 이론이라고도 한다.

6. Reference

1) 대한화학회, 표준 일반화학실험 제 7판, 천문각, 2011, pp. 305~310

2) Brown 외 5인 및 화학교재연구회 옮김, 일반화학 제 14판, Pearson 및 자유아카데미, 2019, pp. 432~455

실험 결과 해석을 위해 필요한 개념

단위 세포와 결정 격자

금속성 고체의 결정 구조

1. Chemicals & Apparatus

1) Chemicals

2) Apparatus

피펫(pipett), spatula, culture tube, 100mL 눈금 실린더, beaker, funnel, test tube, 분무기, 면봉, 종이, 채혈기, 뷰렛 또는 유리관

2. Procedure

실험 1 화학 발광 (Chemiluminescent Oscillation)

1) 용액 A, B, C 그리고 D를 각각 15mL씩 100mL 비커에 넣고 물 중탕으로 가열한다.

2) 실험실의 빛을 모두 소멸시킨 뒤 beaker에서 일어나는 일을 관찰한다.

<준비 용액>

용액 A: 0.50M H2O2 (15% H2O2)

용액 B: 0.15M KSCN

용액 C: 6.00810-4M CuSO4

용액 D: 0.100M NaOH + 3.7*10-3M luminol

실험 2 루미놀을 이용한 혈흔 검사법

1) 10mg의 루미놀(luminol), 0.5g의 탄산나트륨(sodium carbonate)를 100mL 비커에 넣고 10mL 증류수에 녹인 후 15% H2O2 5mL를 넣고 잘 섞는다.

2) 위에서 만든 용액을 스프레이식 분무기에 넣는다.

3) 채혈기를 이용해 미량의 혈액을 작은 test tube에 취한 후 1~2mL의 증류수로 묽히고 모세관을 이용해 종이 위에 묽힌 혈액으로 그림, 글씨 등을 그리고 잘 말린다.

* 농도가 너무 묽으면 확인이 어려우므로 약간 진하게 표시한다.

4) 실험실의 빛을 모두 소멸시킨 뒤 luminol 용액이 담긴 분무기로 용액을 뿌린 다음 일어나는 현상을 관찰한다.

3. Data & Result

4. Discussion

실험 1 루미놀 반응 실험 진행 및 결과 분석

대표적인 화학 발광 반응을 관찰하기 위해서 루미놀 반응을 이용했다. 제공받은 실험 순서에서는 루미놀 용액을 직접 만들고 채혈기를 이용해서 실험을 진행하지만, 실제 실험에서는 만들어져 있는 루미놀 용액을 사용했으며, 이미 추출된 돼지 혈액을 사용했다. 혈액 속에 포함되어 있는 철 이온은 루미놀 반응이 더 빨리 진행할 수 있도록 도와준다. 뿐만 아니라 루미놀 용액을 제조할 때 같이 섞어주는 시료들이 왜 사용이 되어야 하는지 등을 루미놀 반응 메커니즘을 살펴보자.

① 루미놀 용액을 만들기 위해 넣어준 탄산나트륨(Na2CO3)은 이온결합 물질이기 때문에 나트륨 이온과 탄산 이온으로 쉽게 분해된다. 하지만, 탄산 이온이 약산인 탄산에서 유래한 이온이므로, 염의 가수분해 현상에 따라 탄산 이온이 물과 반응하여 해당 용액은 염기성이 된다.

염기성 용액에 포함되어 있는 수산화이온과 루미놀을 구성하는 수소원자가 반응하여 루미놀은 두 개의 수소원자를 잃어버리게 된다. 그 결과 질소 원자들은 전기적으로 음성을 띠는 중간체가 형성된다. ② 산소의 전기음성도가 질소가 보이는 수치보다 더 크다. 그래서 질소 원자에 분포되어 있던 전자가 양 끝에 놓여있는 산소로 이동한다. ③ 과산화수소는 물과 산소를 합쳐 제조한 것이기 때문에 분해 반응이 진행되면 물과 산소를 생성물로 갖는다. 하지만, 과산화수소의 분해 반응은 실온에서 잘 진행되지 않으며 이 현상을 관찰하기 위해서는 촉매가 필요하다. 혈흔 검사에서는 혈액 속 헴 구조에 포함된 철 이온이 촉매로 작용을 하여 과산화수소 분해 반응이 진행된다. 그 결과 생성된 산소가 루미놀 중간체와 반응하며 산화-환원 반응이 진행된다. 그 결과 질소 원자에 산소가 결합한 중간체가 형성되는 데 이 물질은 매우 불안정하다. 그래서 질소 원자를 기체의 형태로 내보내며 비교적 안정한 형태를 유지하려고 한다. 그 결과 완전히 안정하지는 않지만 산소가 삼중항 상태에 놓인 중간물을 얻게 된다. ④ 이 과정에서는 계간 교차가 발생하여 물질의 에너지 준위 상태가 변한다. 산소는 상온에서 삼중항 상태($T_1$)로 놓일 수 있으며, 이는 금지 전이를 통해서 단일항 들뜬 상태($S_1$) 로 이동할 수 있다. 물론 이 반응은 금지전이이므로 발생할 확률이 적을 수 있으나, 이는 완전히 발생하지 않는다는 것을 뜻하지는 않는다. 삼중항 상태가 단일항 들뜬 상태보다 더 낮은 에너지 준위를 가지므로 이 과정에서 스핀 다중도가 변하는 전자 전이가 발생하였다 하더라도 방출되는 빛을 관찰할 수는 없다. 만약 흡수 스펙트럼을 관찰한다면 해당 에너지 차이만큼의 빛이 흡수되는 것을 관찰할 수는 있을 것이다. ⑤ 단일항 들뜬 상태에 놓여있는 물질은 그 상태를 유지할 수 있는 시간이 매우 짧기 때문에 바닥 상태로 내려오게 되며, 이때 에너지를 방출한다. 들뜬 루미놀이 방출하는 에너지의 형태는 빛이며 $S_1$에서 $S_0$으로 에너지 준위가 변화는 과정을 수반하므로 형광 스펙트럼을 얻을 수 있다. 실제로 얻은 실험 결과 에서 확인할 수 있듯 청백색의 파장을 확인할 수 있으며, 이는 형광을 방출하는 것을 의미한다. 해당 그림을 자세하게 보면 혈액으로 모양을 만든 부분을 제외한 다른 부분에서도 형광이 관찰된다. 즉 루미놀 반응은 몇 가지 한계점을 갖고 있음을 알 수 있다. 우선, 루미놀 용액을 사용 직전에 만들어야 정확한 결과를 얻을 수 있다. 이번 실험에 한정하여 루미놀 반응이 진행되기 위해서는 산소 등 산화-환원 반응이 진행할 수 있도록 하는 물질이 필요하다. 이번 실험에서는 이를 위해서 과산화수소의 분해 반응을 이용하나, 과산화수소 분해반응이 느리다는 것과 자발적이라는 것은 별개의 문제이다. 루미놀 용액이 오래전에 만들어졌다면, 혈액 등 촉매와 반응하지 않더라도 내부에서 산화 환원 반응이 진행되어 혈흔의 유무와 관계없이 루미놀 용액 그 자체만으로도 화학 발광이 진행될 수 있다. 또한 루미놀 반응을 통해 얻은 형광이 무조건 혈액에 의해서 진행되지 않으며, 과산화수소 분해 반응을 촉진하는 촉매가 포함된 물질에 의한 결과일 수 있다. 루미놀 반응이 혈흔 검사에 주로 사용되는 이유는 혈액에 들어있는 헴 구조 중 철 이온이 과산화수소 분해 촉매로 작용하여 충분한 산화 환원 반응을 진행시키기 때문이다. 그렇다면 철 이온이 아닌 과산화수소 분해의 촉매인 아이오딘화 칼륨(KI) 용액, 과망가니즈산(MnO2) 용액 등에 루미놀 용액을 넣는다면 마찬가지로 과산화수소 분해 반응이 촉진되어 형광을 관찰할 수 있을 것이다. 이 두가지 한계 때문에 루미놀 반응은 혈액의 유무를 따지는 필요조건이며, 이것이 실제 혈액인지는 추가적인 검사를 요구한다.

실험 2 화학발광 실험의 이해 및 원리

진동 반응은 완전히 평형에 도달하지 않고, 반응지수가 평형 상수보다 크고 작은 상태를 계속해서 반복하는 주기적 반응을 뜻한다. 이번 실험에서 진행한 실험에 대한 현상을 먼저 이해하기 전, 루미놀이 제외된 H2O2-KSCN-CuSO4-NaOH의 진동 반응에 대해서 간단하게 살펴볼 필요가 있다. 해당 진동 반응은 NaOH에 의한 염기 상태 하에서 H2O2-KSCN와 H2O2-CuSO4 사이의 피드백 네트워크에 의하여 진동 반응이 발생한다. 그 결과로 용액의 색 변화, 과산소이온(O2-)의 용해도 변화, 그리고 전위 사이의 변화가 수반된다. 다만, 루미놀이 이 진동계에 첨가되면 보이는 현상이 약간 변화한다. 우선 루미놀의 화학 발광에 의해서 빛이 주기적으로 방출될 수 있다. 앞서 살펴본 루미놀 반응 메커니즘을 이용해서 설명해보도록 하자. 루미놀이 염기성 용액에 놓이면 전하를 갖게 된다. 그리고 산화-환원 반응을 거쳐서 발광을 하게 된다. 해당 진동계에서 과산화수소 분해가 촉매인 황산 구리에 의해서 분해될 때 형성되는 중간체 HO2-Cu(Ⅰ)와 과산소이온 O2-이 해당 산화 환원 반응에 기인한다.

그림 9를 살펴보면 산화-환원 반응에 기인하는 물질들이 서로 증감이 반대로 배치된 것을 확인할 수 있다. 즉, 주기적으로 산화 환원 반응이 진행되어 발광 형태도 주기적으로 발생할 수 있음을 뜻한다. 발광의 주기성 뿐만 아니라 용액 자체의 색 변화에도 변화가 생기는 데, 루미놀이 추가되면 루미놀이 수산화이온과 반응하여 어두운 보라빛을 띠는 중간체를 형성하기 때문에 용액의 색변화가 노란색-무색 관계에서 노란색-어두운 보라색 관계로 변화한다. 한편, 진동 반응이 계속 진행되면서 루미놀이 계속 반응에 참여하기 때문에 진동이 진행될수록 관찰되는 빛의 세기는 약해지고, 반응도 점점 평형에 다다른다. 이 과정을 보다 정확하게 관찰하려고 했으면, 결과 사진으로 형광을 보이는 사진이 아닌 동영상을 촬영하는 것이 도움이 더 되었을 것이다. 그리고 발광 현상 말고, 용액 자체의 색 변화도 관찰하기 위해서 빛을 끄지 않은 상태에서 실험을 진행하여 그 결과를 관찰하는 것도 도움이 되었을 것이다. 그리로 반응계의 농도가 한쪽으로 치우치지 않도록 stirring bar를 이용해서 혼합한 용액을 섞는 것이 더 나은 실험 결과를 얻는 데 도움이 되었을 것이다.

5. Reference

1. 박종진 외 2인, 광화학의 이해, 자유아카데미, 2011, pp. 3~10, 19~33, 35~40, 45~46, 61~67

2. 대한화학회, 표준 일반화학실험 제 7판, 천문각, 2011, pp. 89~95

3. Simeen Stattar 외 1인, Interaction of Luminol with the Oscillating system H2O2-KSCN-CuSO4-NaOH, 1990, 275~277

4. Supavadee Kiatisevi 외 1인, Study of the oscillation and luminol chemiluminescence in the H2O2-KSCN-CuSO4-NaOH system, 2010, 173~177

5. Hernan E. Prypsztein, Chemiluminescent Oscillating Demonstrations: The Chemical Buoy, the Lighting Wave, and the Ghostly Cylinder, 2005, 53~54

실험 결과 해석을 위해 필요한 개념

분자 오비탈

전자 배치

바닥 상태와 들뜬 상태의 스핀 다중도

화학 발광과 화학 진동

복사 과정과 비복사 과정

혈액의 조성과 루미놀 시험

1. Introduction

이번 실험에서는 다양한 종류의 전기영동 방법 중 gel을 쉽게 만들 수 있는 Agarose gel 전기 영동을 이용해서 주어진 Sample DNA를 분리하도록 했다. 우선 전기영동에서 고정상으로 사용할 gel을 합성하려고 Agarose와 1x TAE buffer 25mL를 혼합했다. 이동상으로도 같은 buffer를 사용하는데, 적당히 pH를 조절해서 DNA가 해리되는 것을 방지하며, Tris base로 DNA가 이동할 수 있는 양이온이 제공되며, EDTA로 금속이온을 제거해서 DNA가 손상되는 것을 막을 수 있기 때문이다. TBE buffer으로도 gel을 합성할 수는 있었지만 분해능이 TAE보다 약하므로, 이동상과의 화학적 성질의 차이를 최소화하기 위해서 TAE buffer를 용매로 사용했다. Agarose를 모두 녹이기 위해서 전자레인지를 사용했다. 전자레인지를 사용하게 되면 고립된 공간에서 빠르게 열을 발생시키기 때문에 Agarose를 빠르게 용해할 수 있으나, 갑작스럽게 끓어오르는 것을 방지하기 위하여 랩을 씌운 후 구멍을 조금 뚫어서 빠른 용해와 끓어오름을 방지했다. DNA의 전개 정도를 뚜렷하게 관찰하기 위해서 이번 실험에서는 UV-trans illuminator을 사용한다. EtBr은 뉴클레오타이드 사이의 수소결합에 관여하여 형광정도를 크게 증가하도록 할 수 있다. 이 물질을 gel을 합성할 때 같이 섞어주면 DNA가 전기영동 시 이동하면서 gel에 들어있는 EtBr과 반응할 수 있기 때문에 gel에 섞어주곤 한다. 하지만, 이 물질은 독성이 있으며 DNA의 이동에 영향을 줄 수 있으므로 대체 물질인 RedSafe를 gel을 합성할 때 섞어주었다. 이를 넣기 위해서 micropipette을 사용하는데, 정확한 양을 옮기도록 했기 때문이며 소개된 사용 방법을 따라서 시약을 옮겨 넣었다. 용액을 굳혀 gel을 만들기 위해서 Gel casting plate에 기포가 생기지 않도록 gel을 부었다. 그리고 gel을 넣을 때 tray와 gel casting plate 사이에 공간이 발생하여 합성 중 기포가 발생해 gel에 섞여 들어갈 수 있으므로 이를 방지하기 위해서 둘을 밀착시켜 남은 기포를 제거했다. 그리고 불순물과 같은 먼지를 tip을 이용해서 제거해서 최대한 순수한 gel로 굳히고자 했다. 후에 Loading시 시료를 넣을 자리를 만들기 위해서 Comb를 꽂은 후 gel을 식혀 굳혔다. gel이 완성되면 전기영동을 진행하기 위해서 gel box에 넣는다. 이때 DNA가 전기적으로 음성임을 고려해서 well을 음극을 향하게 배치하여 전기영동시 DNA가 이동거리를 충분히 확보할 수 있도록 했다. 실제로 전기영동을 진행할 DNA는 너무 가볍기 때문에 그냥 well에 집어넣으면 buffer에 흘러나갈 수 있기 때문에 이를 방지하기 위해서 loading dye를 섞어준다. 다만 또 너무 무거운 물질이 포함된 dye는 전기 영동을 방해하기 때문에 큰 영향을 주지 않는 정도의 dye를 사용해야 한다. 그리고 dye를 이용해서 UV-trans illuminator을 사용하지 않고도 어느정도 전기 영동이 진행되었는지 판단하기 위해서 사용하기도 한다. e-tube에 sample과 loading dye를 섞기 위해서 tapping과정이 필요하며, 시료의 양이 매우 적으므로 약하게 혼합을 진행해야 한다. well이 찢어져서 gel을 다시 만들지 않도록 조심해서 well에 시료와, 전개된 정도에 따른 비교 및 DNA의 종류를 결정짓기 위해서 100bp plus ladder를 대조군으로 넣었다. 적당한 시간이 지난 후 실험 결과를 확인하기 위해서 UV-trans illuminator에 gel을 옮겼다. 이때 기포가 생기도록 gel을 놓으면 산란 현상 때문에 뚜렷한 결과를 확인하기 힘들기 때문에 이를 감안하여 기포가 생기지 않도록 조심하게 내려놓았다.

2. Chemicals & Apparatus

1) Chemicals

1x TAE buffer, 6x loading dye, DNA ladder, Agarose, DW(증류수), RedSafe

* nx 용액: 실험에서 사용하는 농도보다 n배 진한 용액

2) Apparatus

Gel box, Gel casting tray, Microwave, UV-trasn-illuminator, Erlenmeyer flask, Micropipette E-tube

3. Procedure

실험 1 Agarose Gel 만들기

1) 두 조당 하나의 gel을 사용한다.

2) Gel casting tray와 comb, 플라스크를 깨끗이 씻는다.

3) Agarose 0.25g과 1x TAE buffer 25mL를 100mL삼각 플라스크에 넣고 랩으로 막은 후 tip으로 구멍을 여러 개 뚫는다.

4) 45초 정도 데운 후 얼마나 녹았는지 확인한다. 이후 15~30초씩 데우면서 agarose가 완전히 녹을 때까지 데운다. 꺼내어 흔들었을 때 투명하고 작은 알갱이들도 다 녹여야 한다. 필요 이상으로 오래 데워서 물이 증발하면 농도가 진해져 영동 속도가 느려 진다.

* 플라스크가 뜨거우므로 목장갑을 사용한다.

5) 혼합용액에 RedSafe 1.3μL를 넣어준다.

6) Gel틀에 기포가 생기지 않게 천천히 용액을 부은 후 노란 tip 뒷부분으로 tray를 누르고 일정한 방향으로 밀어서 밑의 공기를 뺀 후 떠있는 기포도 모두 제거한다.

7) Comb를 꽂은 후 20~30분 정도 굳힌다.

* 플라스크에 남은 용액이 굳으면 씻어내기 까다로우니 바로 세척할 것

실험 2 Agarose gel Electrophoresis

1) 굳힌 gel의 well이 망가지지 않도록 조심스럽게 comb를 뽑고 tray채로 gel box에 넣는다. 이때, well이 (- )극을 향하도록 한다.

2) Gel box에 Gel이 잠길 정도로 1x TAE Buffer를 넣는다. (Tray 기준 빨간 점선 사이까지만 채우면 충분하다.)   

3) 새 e-tube에 준비된 DNA sample 3μL과 6x Loading Dye 0.6μL를 넣는다.

4) DNA는 충격에 약하므로 tapping하여 섞는다.

5) Well에 100bp plus ladder 4μL, sample 3μL씩 load한다. 팁으로 gel을 찢거나 뚫지 않도록 주의한다.

6) 20~30분 동안 Ful Voltage로 Gel Run을 진행한다.

실험 3 UV-trans illuminator로 결과 확인하기

1) Ethanol로 illuminator 위를 깨끗이 닦는다.

2) Ethanol이 마르면 젤을 cast에서 조심스럽게 떼어 illuminator에 올려놓는다. 이때 gel 아래에 공기가 들어가면 적당히 움직이거나 눌러 공기를 뺀다.

3) 덮개를 덮고 불을 끈 후 illuminator를 켜서 관찰한다.

4. Data & Result

5. Discussion

전기영동 실험의 결과는 크게 2가지로 해석할 수 있다. 첫 번째는 sample DNA가 이동하여 형성된 bend의 선명도 및 진행 경로 등을 보는 것이다. 그리고 두 번째는 각 시료와 ladder가 얼마나 진행하여 분리하고자 했던 시료가 어떤 물질에 해당하는 지 비교하는 것이다. 첫 번째 관점에서 실험 결과를 살펴보자. 그림 9에서 ladder와 sample A와 B 모두 형광색이 명확하게 발현되었음을 확인할 수 있다. 이를 통해서 전기 영동 장치에 전압이 적절히 걸려 있고, 첨가한 샘플의 양이 적절했으며, 실험과정 중 well이 잘 형성되었음을 알 수 있다. 두 번째 관점에서 실험 결과를 살펴보도록 하자. 원래는 ladder이 분리된 것을 기준으로 각 시료가 이동한 정도를 비교해서 사용한 시료 당 포함된 DNA의 질량 및 그 DNA의 염기쌍 포함 정도를 알 수 있다. 이번에 사용한 gel이 정확히 1.5% TAE Buffer Agarose gel은 아닌 것을 감안하더라도 그림 10과 그림 9의 ladder에서 나타난 band의 개수가 다르기 때문에 전기 영동이 충분히 이루어지지 않음을 확인할 수 있다. 물론 실험에서 사용한 sample A와 B와 비교해봤을 때 각각에 대응하는 band가 있다. 그러나 ladder가 정확하게 분리가 되지 않았기 때문에 염기쌍 및 DNA의 질량을 결정지을 수는 없다. 다만 Theory에서 소개한 Stokes 공식에 따라서 A와 B의 상대적인 정보의 평가만 가능할 뿐이다. Stroke식과 각 변수가 의미하는 바를 다시 정리해보자.

이때 같은 시간동안 전기 영동을 진행했으므로 각 시료가 이동한 거리와 속도가 비례하는 것을 이용할 수 있다. 그리고 같은 조건에서 전기영동을 진행했기 때문에 몇 가지 변수들은 모두 상수로, 거리에 차이가 발생하는 것에 영향을 주지 않을 수 있다. 이 변수들은 , 그리고 에 해당하여 상수로 표현된다. 따라서 각 시료의 이동 거리는 와 사이의 비율에 의하여 결정되는 것을 확인할 수 있다. 두 변수는 서로 비례관계에 놓여있기 때문에 정확한 수치적 비교는 할 수 없다. 다만 더 많은 거리를 이동한 sample A가 sample B보다 크기에 비해서 더 음의 전하를 나타내는 것 밖에 얻어낼 수 없다.

6. Reference

1) 강호일, 전기영동 최신 프로토콜, 월드사이언스, 2006, pp. 14~25

실험 결과 해석을 위해 필요한 개념

DNA의 구성 및 구조

전기영동의 개념과 물질 이동 속도 결정

전기영동의 종류

Gel loading dye